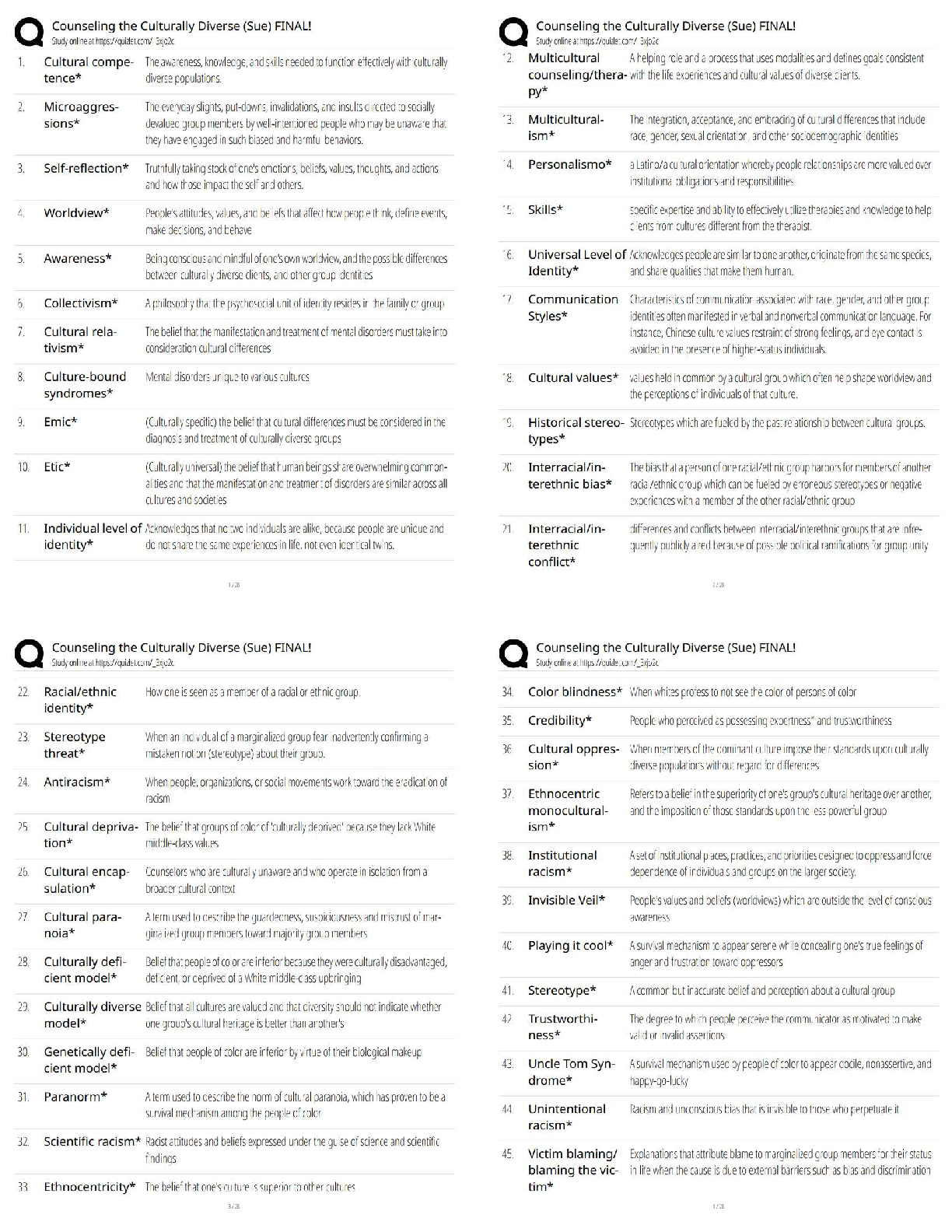
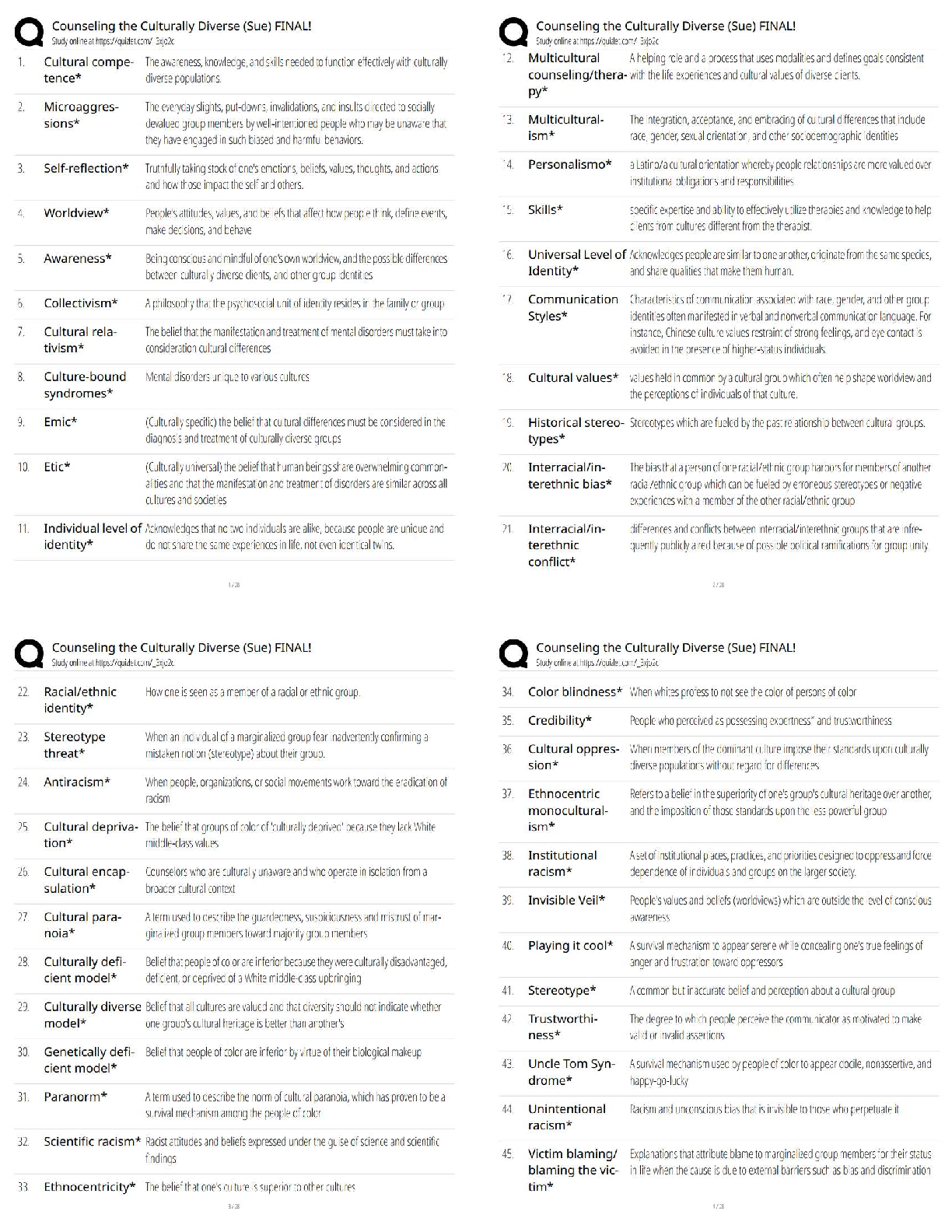
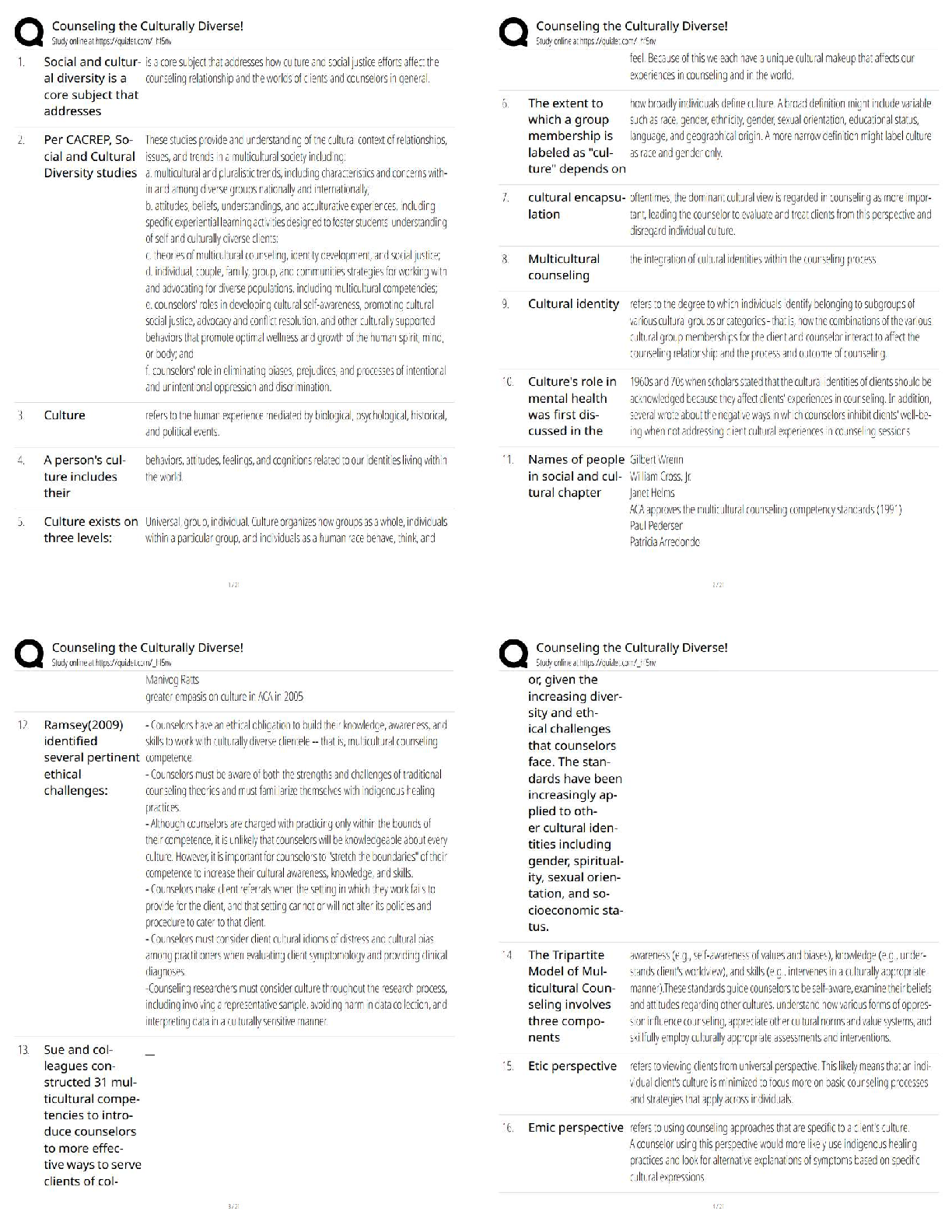
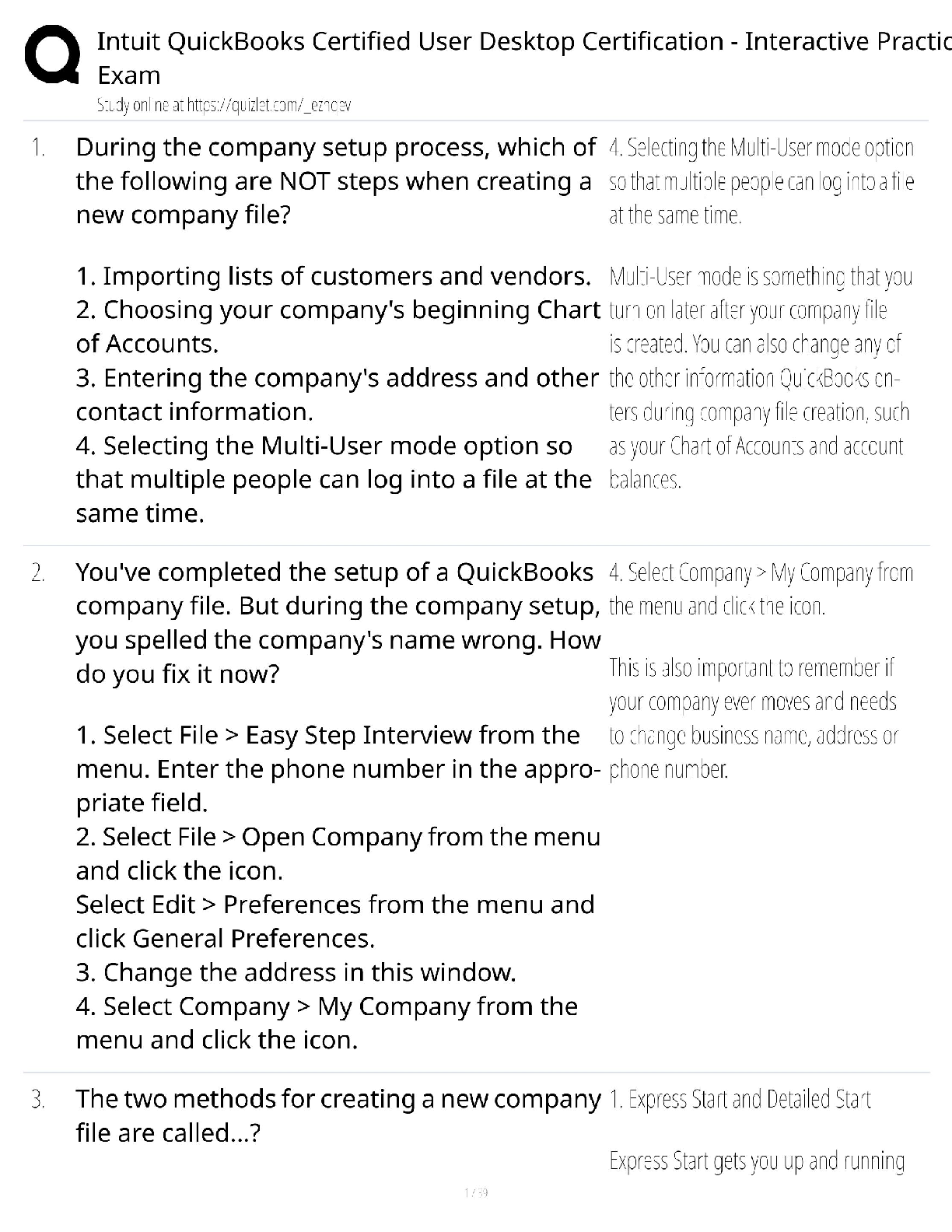
1. Chapter 13, numbers 13.6, 13.8, 13.9, and 13.10
13.6, It’s well established, we’ll assume, that lab rats require an average of 32 trials in a complex water
maze before reaching a learning criterion of three consecut
...
1. Chapter 13, numbers 13.6, 13.8, 13.9, and 13.10
13.6, It’s well established, we’ll assume, that lab rats require an average of 32 trials in a complex water
maze before reaching a learning criterion of three consecutive errorless trials. To determine whether a
mildly adverse stimulus has any effect on performance, a sample of seven lab rats were given a mild
electrical shock just before each trial.
(a) Given that X = 34.89 and s = 3.02, test the null hypothesis with t, using the .05 level of
significance.
Ho: u = 32
Ha: u # 32
-----
t= (34.89-32)/[3.02/√ (7)] = 2.532
df= 7-1=6
p-value = P(t6< 2.532) = 0.0223
p= 2 x 0.0223 = 0.0446
---
Conclusion: Since the p-value is less than 5%, reject Ho. This means that the shock
treatment has caused a change in the results water maze study.
(b) Construct a 95 percent confidence interval for the true number of trials required to learn the
water maze.
x-bar = 34.89
Margin of Error = 1.96
-----
95% CI: 34.89 - (1.96) (3.02) < u < 34.89 + (1.96) (3.02)
95% CI: 28.97< u < 40.81
(c) Interpret this confidence interval.
We have 95% confidence that the number of trials required is between 28.97 and 40.81
13.8 Assume that on average, healthy young adults dream 90 minutes each night, as inferred from
measures, including rapid eye movement (REM) sleep. An investigator wishes to determine whether
drinking coffee just before going to sleep affects the amount of dream time. After drinking a standard
amount of coffee, dream time is monitored for each of 28 healthy young adults in a random sample.
Results show a sample mean, X, of 88 minutes and a sample standard deviation, s, of 9 minutes.
(a) Use t to test the null hypothesis at the .05 level of significance.
H0: mu = 90
H1: mu ≠ 90
----
Our one sample t-test statistic is
t = 88-90 / (9/√28)
= -2/1.701
= -1.1759
-------
df= 28-1=27
p-value = P(t27> -1.1759) = 0.12495
p= 2 x 0.12495= 0. 2499
p-value = 0.2499
Since calculated p value > 0.05 at 5% significance level, we do not reject H0 and conclude
that drinking coffee does not affect the amount of dream time.
(b) If appropriate (because the null hypothesis has been rejected), construct a 95 percent
confidence interval and interpret this interval.
The null hypothesis has not been rejected, so there is no need to construct a 95 percent
confidence interval.
This study source was downloaded by 100000831988016 from CourseHero.com on 05-02-2022 07:29:26 GMT -05:00
https://www.coursehero.com/file/18280295/Week5/
13.9 In the gas mileage test described in this chapter, would you prefer a smaller or a larger sample size if
you were
(a) the car manufacturer? Why?
(b) a vigorous prosecutor for the federal regulatory agency? Why?
13.10 Even though the population standard deviation is unknown, an investigator uses z rather than the
more appropriate t to test a hypothesis at the .05 level of significance.
(a) Is the true level of significance larger or smaller than .05?
(b) Is the true critical value larger or smaller than that for the critical z?
2. Chapter 14, numbers 14.11, 14.12, and 14.14
14.11 Each subject earns a score between 0 and 30. A score of 0 signifies the subject’s unwillingness to
comply at the very outset, and a score of 30 signifies the subject’s willingness to comply completely with
the experimenter’s orders. In one condition, shocks are administered only after an affirmative decision by
the committee, consisting of one real subject and two associates of the investigator, who act as subjects
but in fact merely go along with the decision of the real subject. In the other condition, shocks are
administered only after an affirmative decision by a solitary real subject.
A total of 12 subjects are randomly assigned, in equal numbers, to the committee condition (X1) and to
the solitary condition (X2). A compliance score is obtained for each subject. Use t to test the null
hypothesis at the .05 level of significance.
P value and statistical significance:
The two-tailed P value equals 0.5222
By conventional criteria, this difference is considered to be not statistically significant.
Confidence interval:
The mean of Committee minus Solitary equals 2.33
95% confidence interval of this difference: From -5.51 to 10.17
Intermediate values used in calculations:
t = 0.6632
df = 10
standard error of difference = 3.518
14.12 To determine whether training in a series of workshops on creative thinking increases IQ
scores, a total of 70 students are randomly divided into treatment and control groups of 35 each.
After two months of training, the sample mean IQ (– X1) for the treatment group equals 110, and
the sample mean IQ (– X2) for the control group equals 108. The estimated standard error equals
1.80.
(a) Using t, test the null hypothesis
[Show More]














.png)