1. Chapter 16, numbers 16.9, 16.10, 16.12 and 16.14
16.9
Given the aggression scores below for Outcome A of the sleep deprivation experiment, verify
that, as suggested earlier, these mean differences shouldn’t be take
...
1. Chapter 16, numbers 16.9, 16.10, 16.12 and 16.14
16.9
Given the aggression scores below for Outcome A of the sleep deprivation experiment, verify
that, as suggested earlier, these mean differences shouldn’t be taken seriously by testing the null
hypothesis at the .05 level of significance. Use the computation formulas for the various sums of
squares and summarize results with an ANOVA table.
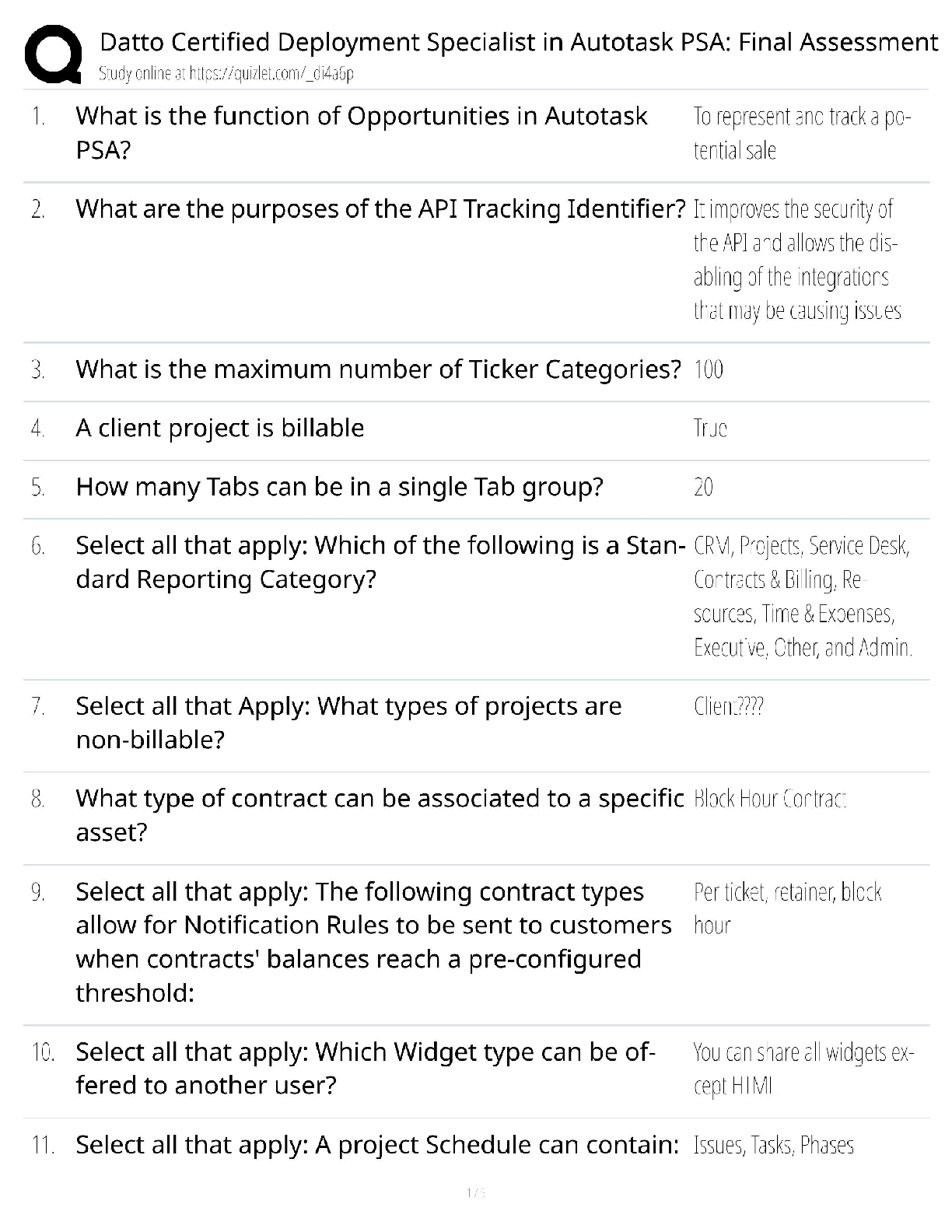
ANOVA: Single
Factor
SUMMARY
Groups
Coun
t
Su
m
Averag
e
Varianc
e
zero 3 15 5 4
twenty-four 3 18 6 4
forty-eight 3 12 4 4
ANOVA
Source of Variation SS df MS F
Pvalue F crit
Between Groups 6 2 3 0.75 0.512
5.1432528
5
Within Groups 24 6 4
Total 30 8
H0: μ
0 = μ
24 = μ
48
H1: H0 is false
Based on this ANOVA Table we would fail to reject the null hypothesis because F=0.75 and
the Fcrit = 5.14325285.
16.10
Another psychologist conducts a sleep deprivation experiment. For reasons beyond his control,
unequal numbers of subjects occupy the different groups. (Therefore, when calculating in SS
between and SS within , you must adjust the denominator term, n , to reflect the unequal numbers
of subjects in the group totals.)
(a) Summarize the results with an ANOVA table. You need not do a step-by step hypothesis test
procedure.
zero twenty-four forty-eight
1 4 7
3 7 12
6 5 10
2 9
1
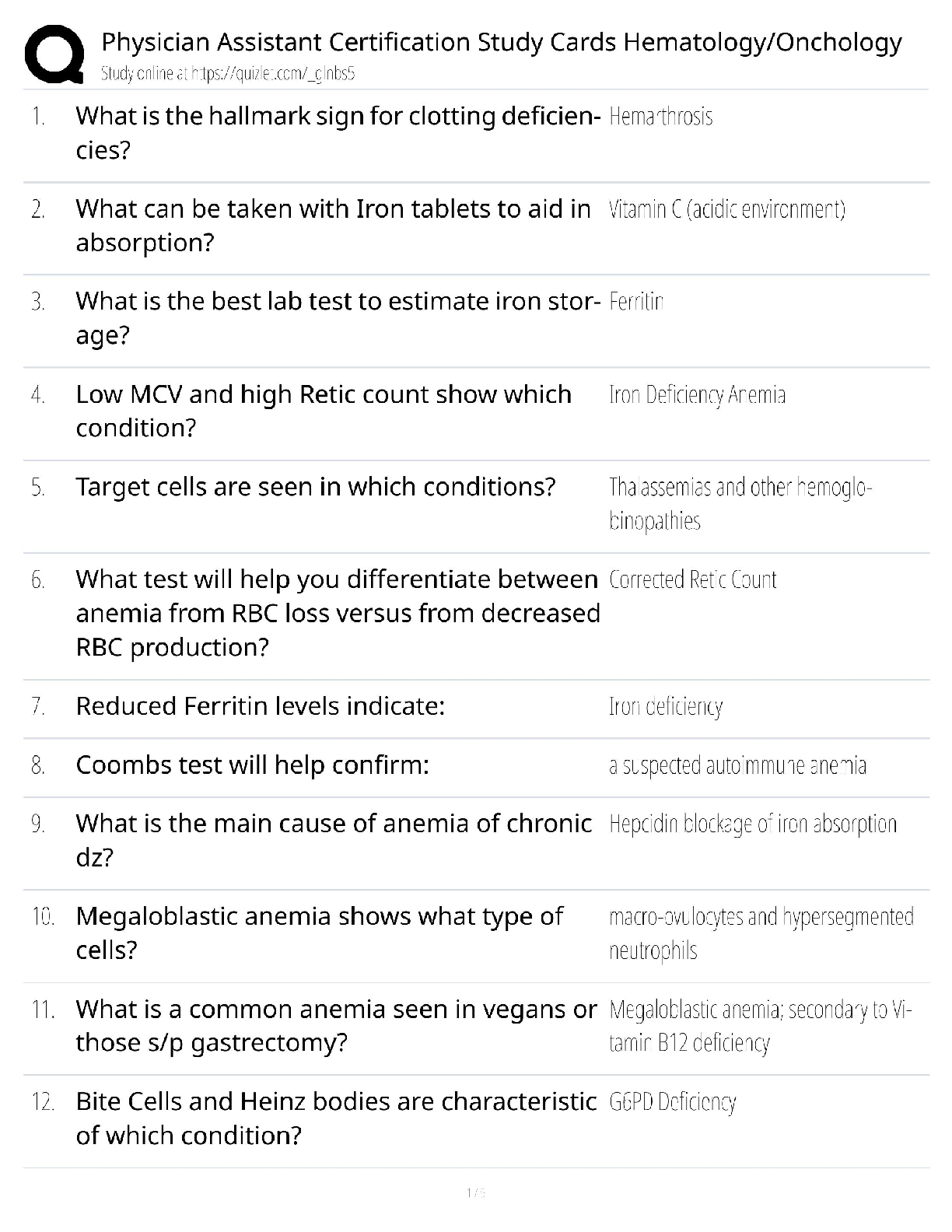
Anova: Single
Factor
SUMMARY
Groups Count Sum Average Variance
zero 5 13 2.6 4.3
twenty-four 3 16
5.33333333
3
2.33333333
3
forty-eight 4 38 9.5
4.33333333
3
ANOVA
Source of Variation SS df MS F P-value F crit
Between Groups 106.05 2 53.025 13.6871414
0.0018643
0 4.256494729
Within Groups
34.8666666
7 9
3.87407407
4
Total
140.916666
7 11
H0: μ
0 = μ
24 = μ
48
H1: H0 is false
Based on this ANOVA Table we would reject the null hypothesis because F=13.6871414 and
the Fcrit = 4.256494729.
(b) If appropriate, estimate the effect size with eta-squared.
2
2= 0.752572 This indicates a large effect size.
(c) If appropriate, use Tukey’s HSD test (with n´ = 4 for the sample size, n)to identify pairs of
means that contribute to the significant F, given that X´
0 = 2.60, X´
24 = 5.33, and X´
48 =
9.50.
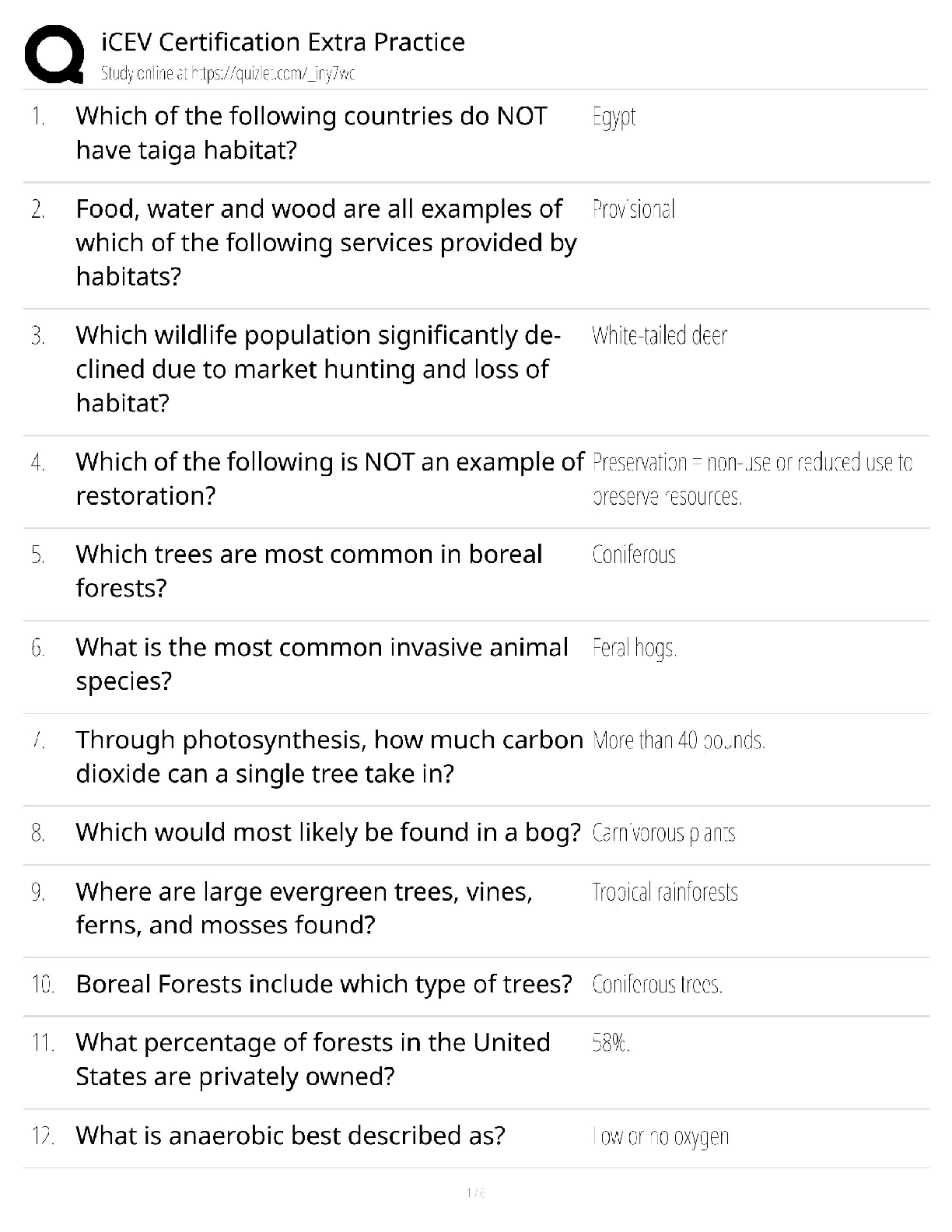
HSD= 3.95*(√3.8740/4) = 3.887327
x0 x24 x48
x0 0 2.73 6.9
x24 0 4.17
x48 0
Only the pairs with 48 hours of sleep deprivation contribute to the significant F.
(d) If appropriate, estimate effect sizes with Cohen’s d.
d(x48, x0)= 6.9/√3.87 = 3.5
d(x48, x24)= 4.17/√3.87 = 2.12
These estimates indicate a large effect size because they are much bigger than .5.
(e) Indicate how all of the above results would be reported in the literature, given sample
standard deviations of s 0 = 2.07, s 24 = 1.53, and s 48 = 2.08.
Aggression scores for subjects deprived of sleep for 0 hours ( X´
0 = 2.60, s 0 = 2.07), for 24
hours ( X´
24 = 5.33, s 24 = 1.53), for 48 hours ( X´
48 = 9.50, s 48 = 2.08) differ significantly [
F (2,9) = 13.70, MSE = 3.87, p < .05, η 2 = .75]. According to Tukey’s HSD test, the mean
differences between the 24- and 48-hour groups (4.17) and between the 0- and 48-hour groups
(6.90) are significant ( HSD = 3.87, p < .05, d = 2.12, 3.50).
*16.12
For some experiment, imagine four possible outcomes, as described in the following ANOVA
table.
(a) How many groups are in Outc
[Show More]