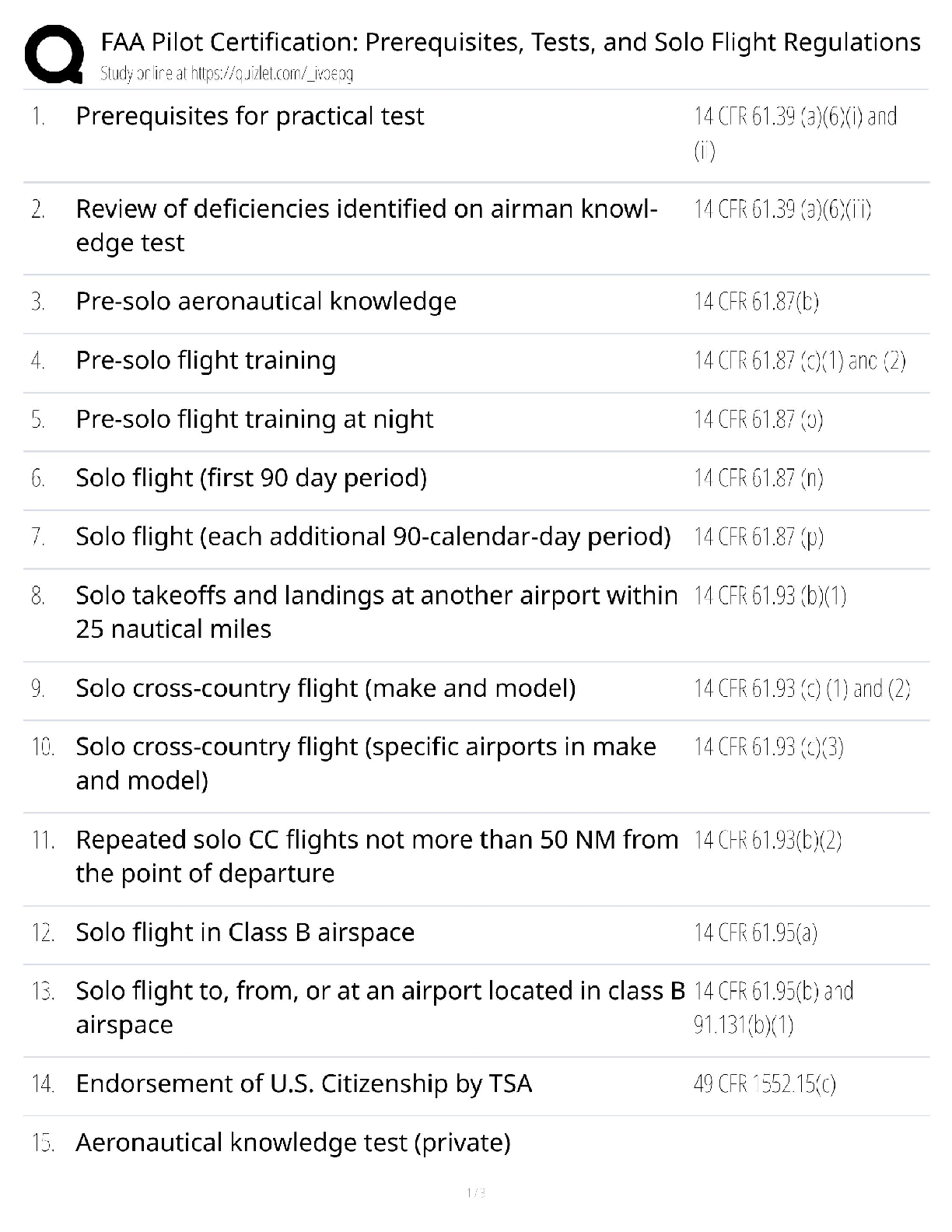
ISYE Midterm 1 Notes:
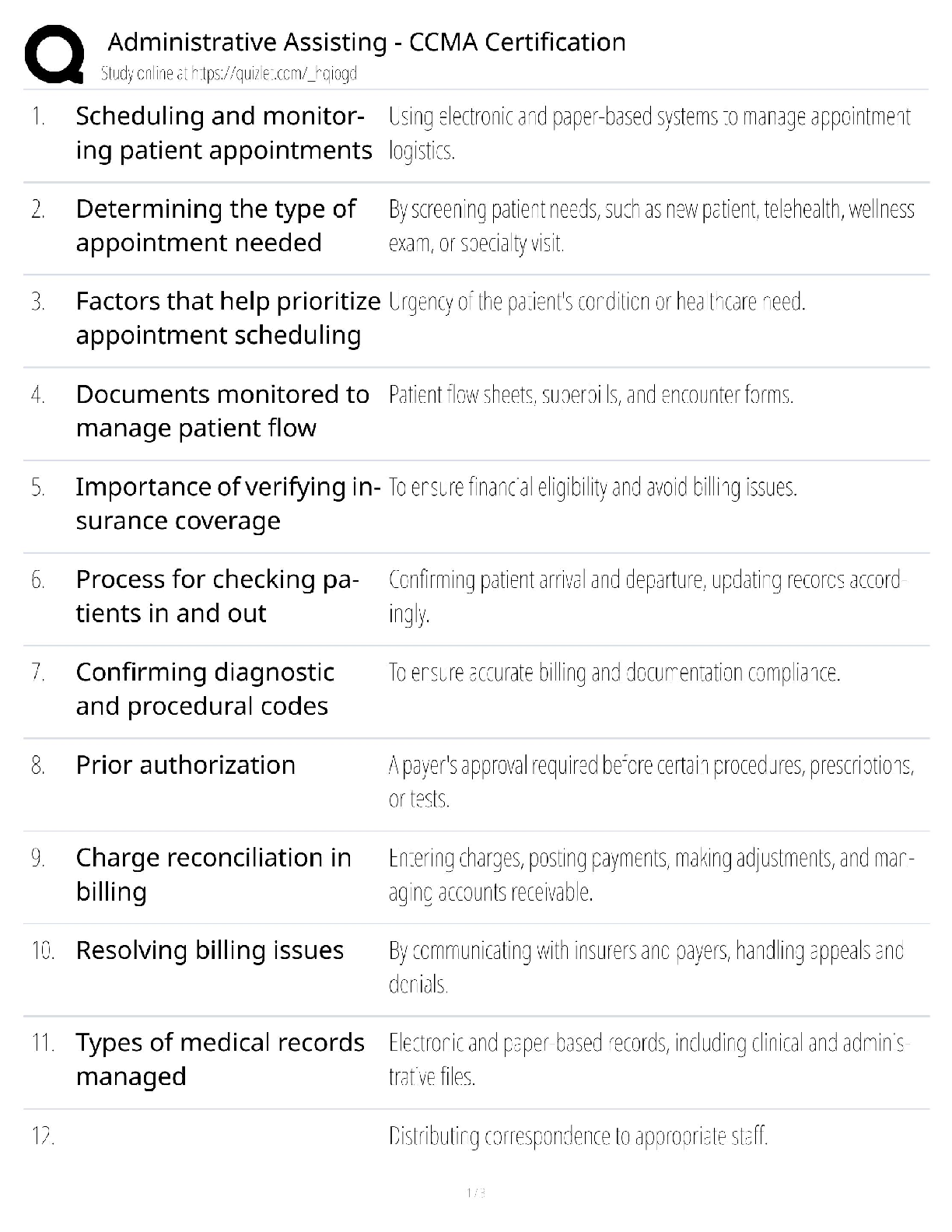
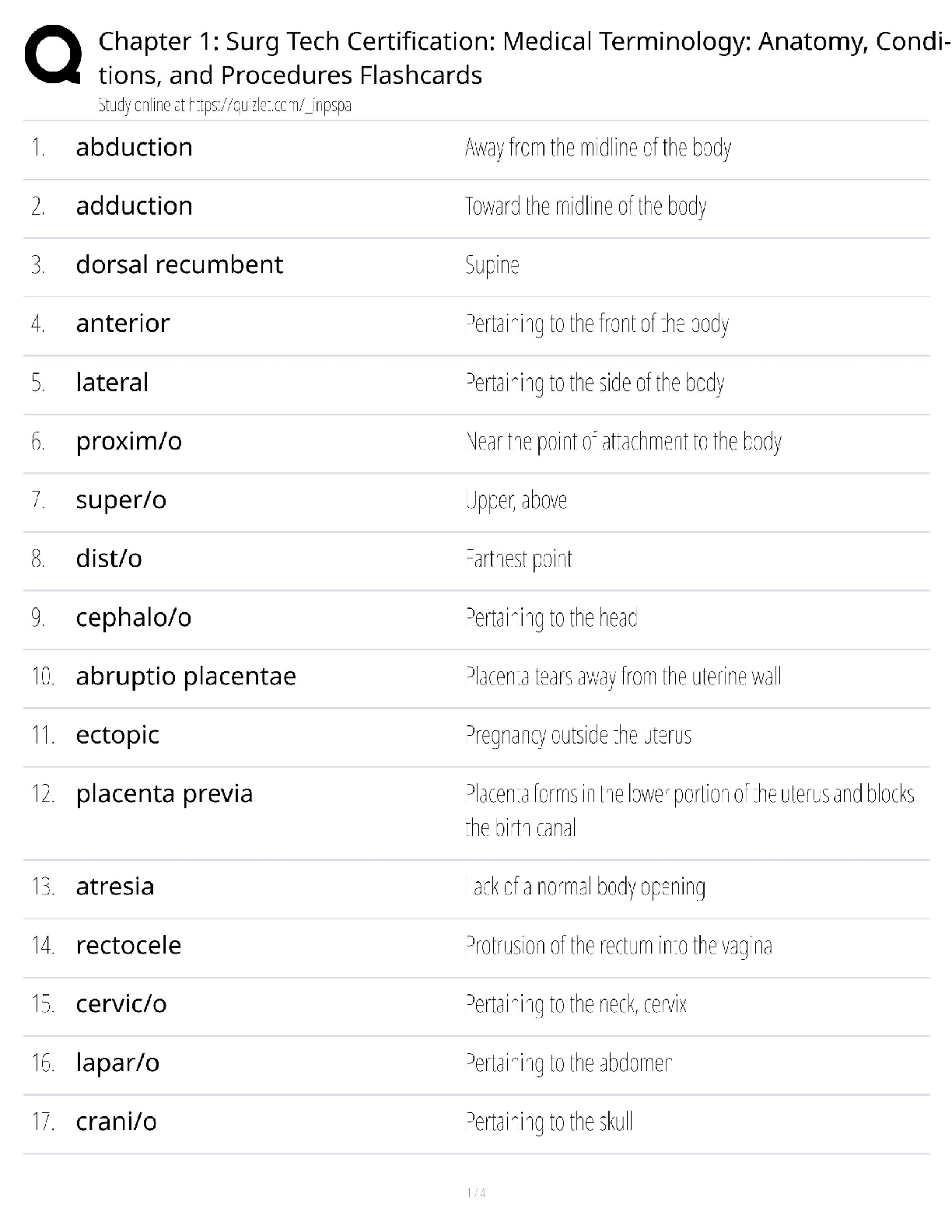
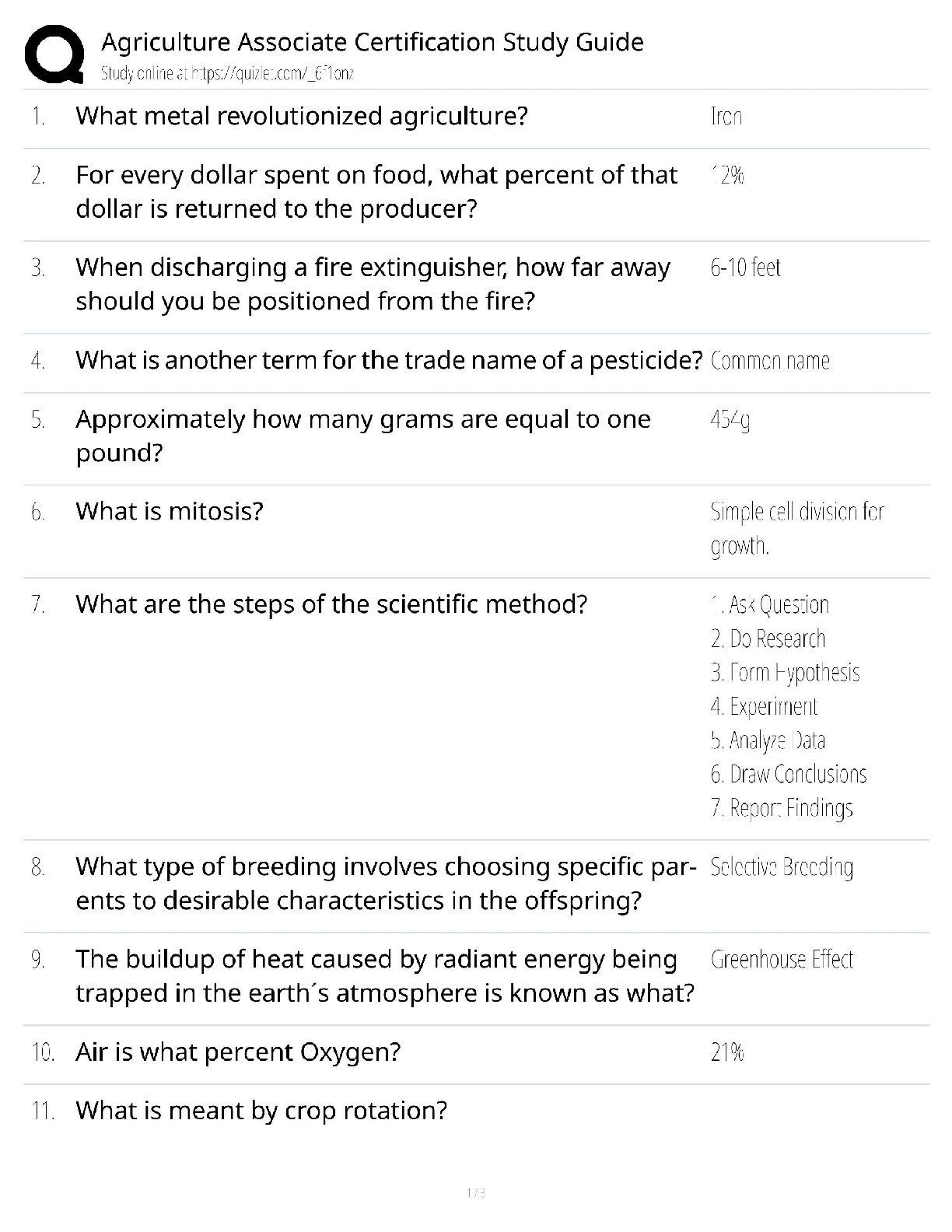
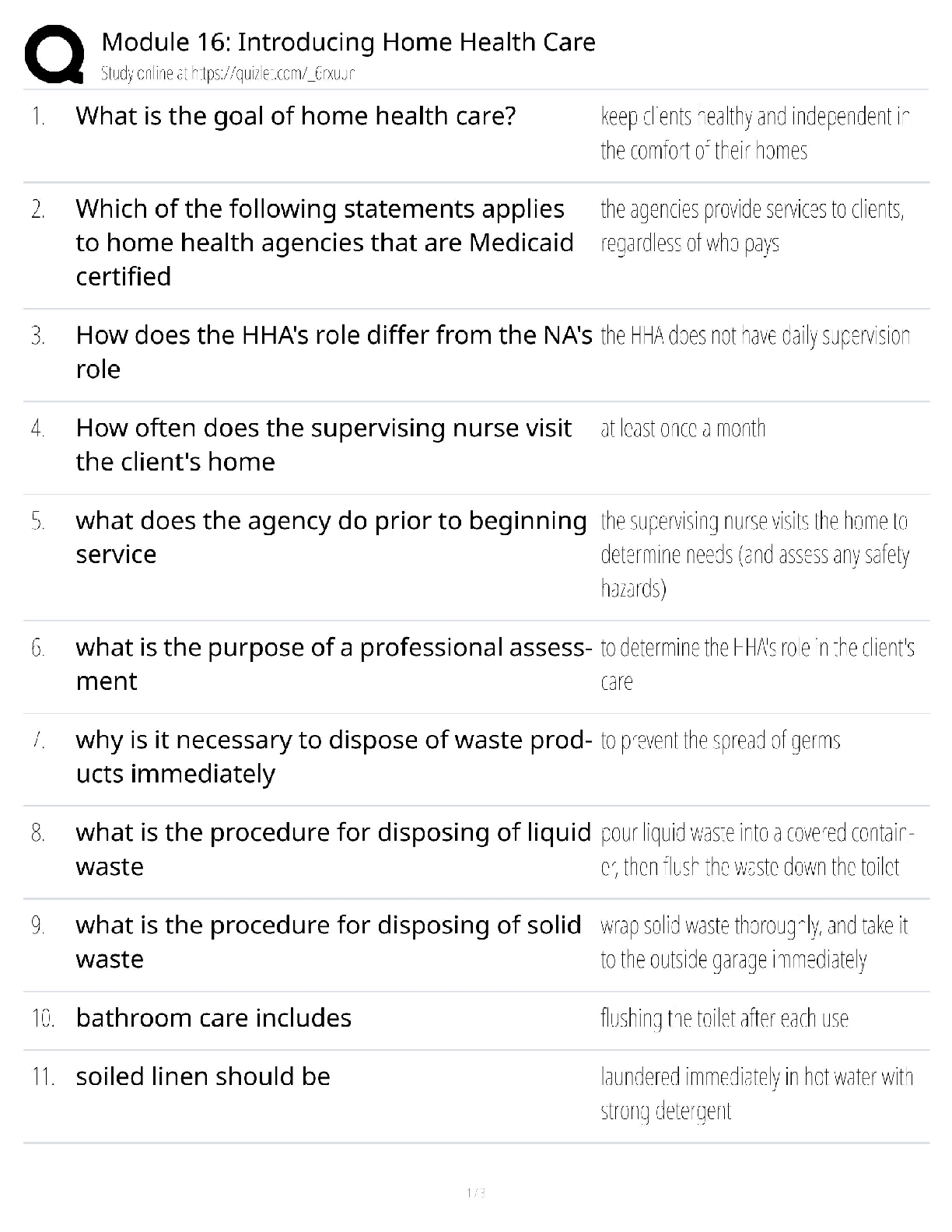
Week 1 Classification:
- Two main types of classifiers:
o Hard Classifier: A classifier that perfectly separates data into 2 (or more) correct classes.
This type of classifier is rigid and is on
...
ISYE Midterm 1 Notes:
Week 1 Classification:
- Two main types of classifiers:
o Hard Classifier: A classifier that perfectly separates data into 2 (or more) correct classes.
This type of classifier is rigid and is only applicable to perfectly separable datasets.
o Soft Classifier: A classifier that does not perfectly separate data into perfectly correct
classes. This type is used when a dataset it not realistically separable by class thus we
use a more flexible classifier that gives us not a perfect, but optimal solution given the
constraint of a-separability.
- If a given model uses a soft classifier, we can further tune it to fit our needs based on factors
such as the cost of misclassification.
- Semantics on the types of data:
o Columns: Attribute / Features / Response / Covariates / Predictor
o Rows: Observations / Data point
o Structured Data: data that is described and stored in a structured way
o Unstructured Data: data cannot be described or easily stored. The most common
example is written language.
o Quantitative Values: Numbers that have meaning in a numerical sense
o Categorical Data: can be numeric representing a category or non-numeric indicating a
category
o Unrelated Data: No relationships between datapoints
o Timeseries Data: Same data recorded over time typically in regular intervals
- Hyperplane: In a p-dimensional coordinate space, a hyperplane is the flat affine subspace of that
dimension such that it takes a dimensionality of (p-1). In this context affine indicates that the
subspace need not pass through the origin. This equation will be in general linear form.
o Equation of p dimensional general form:
β0 + β1X1 + β2X2 + … + βpXp = 0
- Linear Separable Hyperplane: Given a set of datapoints with given signed classes and perfectly
linearly separable classes, there will be an infinite number of hyperplanes equations that satisfy
all points being classified correctly. This is demonstrated in the constraints below. If a point is
above the hyperplane it will have a positive value and if it is below the separating hyperplane it
will have a value less than zero. Furthermore, if the class is correctly predicted via the result of
the equation it will share the sign of its respective yi value. Given these two properties of the
hyperplanes we can infer the following constraints.
If yi = 1; β0 + β1X1 + β2X2 + … + βpXp > 0
If yi = -1; β0 + β1X1 + β2X2 + … + βpXp < 0
o We can equivalently rewrite these two inequalities into a single property of the
hyperplane by combining them via a class wise multiplication term. This multiplication
causes no change as we have perfect sign translation without class error.
(Yi) (β0 + β1X1 + β2X2 + … + βpXp) > 0
o The above equation/constraint verifies that all points are properly classified.
o There will be many linear equations that satisfy this equation, but we need to thin this
solution space down. Thus, in order to select the best one, we need to refine the
optimization problem constraints to find the optimal hyperplane that separates the
classes by the maximum amount which we will call margin.
- Margin: In the case of SVM, we define margin as the distance between the classes and their
decision boundary. Consider the previous equation for a hyperplane and consider it has 2
parallel lines equidistant from one another via a distance M. This distance M can be calculated
using the formula for the distance between parallel line:
o M = 2 / (sqrt (∑ ai
2
))
o In this case we are going to expand the margin as much as possible so that there is
maximum separation between classes. This optimization is gone about by minimizing the
denominator of M which is the sum of all coefficients squared. By minimizing the sum of
coefficients, we can maximize the distance between classes while our previous
constraint continues to enforce that all classes are still correctly classified. This will yield
a maximum margin classifier.
- Maximal Margin Classifier: The hyperplane that optimal separates the points into the correct
classes with the greatest margin between the decision boundary:
o Maximize: Margin~ M ~ 2 / (sqrt (∑ ai
2
))
o By Minimizing: ∑ ai
2
o Or by setting a constraint: ∑ ai
2
= 1
o Constrained by: (Yi) (β0 + β1X1 + β2X2 + … + βpXp) ≥ M
o Collectively, this optimization problem lays out that all points be classified correctly with
enough distance from misclassification as specified by the margin amount that satisfies
the inequality relative to its maximized magnitude.
o The points that lie upon the margin equations are support vectors and are equal to the
margin that has been maximized.
- Support Vector Machine: In this variant of a maximal margin classifier, we face a dataset with
non-linearly separable classes. Due to this fact we must allow violations of both the response
and the margin. We assign a cost value to each type of error and optimize the equation to the
following:
o Minimize: Λ * ∑ max {0, 1 – (∑ aixij + a0) (yi)} + λ ∑ ai
2
o Λ a term multiplied by the classification error (larger if misclassification more costly)
o Λ a term multiplied by the margin magnitude (large if margin violations more costly)
o The first term quantifies the magnitude if any of the classification errors
o The second term quantifies the cost of margin violation via the lambda term
o Thus, a small lambda makes margin violations less impactful leaving more budget for
errors in the classification error term as a margin violation is less costly.
o On the other hand, a large lambda leaves little room for the classification error term and
instead prioritizes maximal margin as a violation is more costly.
o The total error will be equal to C also considered a budget of error.
o In SVM C is our cost tuning parameter that caps the sum of error terms to a desired
budget.
o This concept can be driven beyond linear decision boundaries and into a non-linear
decision boundary which is accomplished via the implementation of kernel functions
which use matrix multiplication operations to expand the given feature space into higher
order dimensions and terms. Examples include RBF dot (radial kernel) or polydot
(polynomial expansion kernel)
- SVM usually requires data adjustment operation otherwise differences in factor magnitude
values could be detrimental to model interpretation and cost optimization. Most used method of
accounting for this is scaling global making all coefficients interpreted in the same fashion.
- Scaling: a data adjustment taking a feature from one range to another interval such as 0 to 1 or
min to max scaling:
o Min – Max Scaling:
o Xij scaled = (xij – xmin j) / (xmax j – xmin j)
- Standardizing: scaling a feature or dataset by a normal distribution. This typically involves taking
the mean and standard deviation of all observations of a factor then standardizing each value by
the mean and standard deviation in the observed factor distribution
o Xij standardized = (xij – mean(xj)) / σj
o This type of standardization is commonly used with mean=0 and standard deviation = 1.
- Use cases for each form of data scaling:
o Scaling: For some models it is important for your data to be within a bounded range for
practical purposes. Such an example might be an SAT score, Batting Average, or RGB
color intensities. Additionally, some models require this such as neural networks or
optimization models (otherwise gradient will not converge)
o Standardization: Principal component analysis and clustering often perform better when
standardized rather than scaled. However, this conclusion is not universal there is much
interplay between when and how either could be used
o In most cases either method can be used and justified, and one may perform better than
another under different models etc. Try both and see what is best.
- K-Nearest Neighbor Model (KNN): this type of model is used in classification tasks that require
the classification of more than 2 classes. The model predicts the class of a new point by
determining which of a “k” number of neighbors is most numerous and this point is assigned the
mode of these neighbors. There are however multiple ways of determining which points are
closest to our test point beyond typical Euclidean straight-line distance. Sometimes, we may
have a large feature space in which we use a multidimensional distance metric that weighs the
distance in each dimension via importance. Such weights can be established through variable
selection methods such as regression, lasso, ridge, elastic nets, and PCA. The number “k” is a
tuning parameter used to determine the number of neighbors to rely on. In a suitable large
model, we often test multiple values of “k” via an elbow plot. These values range from 2 to the
root of n datapoints. The use of root n as our maximum value of “k” is a common heuristic.
Week 2 Validation:
- Validation: The process of testing how good a model truly is by exposing it to out of sample data
and discovering objectively how it performs outside of training.
- In data science, you cannot train a model on the same data set you use to measure its
performance. Otherwise we would provide an inaccurate model with a misleadingly high
accuracy level.
- In the training of a model on a given dataset we see two types of effects taken into account:
o Real Effects: true relationships observed by the model present in the data and capable of
describing and predicting events outside its sample
o Random Effects: Things noticed in the sample data that appear real but are in fact just
noise from the training dataset. When taken beyond our sample these effects will
provide misleading results and perform poorly if they comprise a significant amount of
the model’s predictive ability.
- By validating with outside data, we introduce our model to a new set of data with its own
random effects that will differ heavily from the random effects of the first data set. Thus, a model
with a good ability toISYE Midterm 1 Notes:
Week 1 Classification:
- Two main types of classifiers:
o Hard Classifier: A classifier that perfectly separates data into 2 (or more) correct classes.
This type of classifier is rigid and is only applicable to perfectly separable datasets.
o Soft Classifier: A classifier that does not perfectly separate data into perfectly correct
classes. This type is used when a dataset it not realistically separable by class thus we
use a more flexible classifier that gives us not a perfect, but optimal solution given the
constraint of a-separability.
- If a given model uses a soft classifier, we can further tune it to fit our needs based on factors
such as the cost of misclassification.
- Semantics on the types of data:
o Columns: Attribute / Features / Response / Covariates / Predictor
o Rows: Observations / Data point
o Structured Data: data that is described and stored in a structured way
o Unstructured Data: data cannot be described or easily stored. The most common
example is written language.
o Quantitative Values: Numbers that have meaning in a numerical sense
o Categorical Data: can be numeric representing a category or non-numeric indicating a
category
o Unrelated Data: No relationships between datapoints
o Timeseries Data: Same data recorded over time typically in regular intervals
- Hyperplane: In a p-dimensional coordinate space, a hyperplane is the flat affine subspace of that
dimension such that it takes a dimensionality of (p-1). In this context affine indicates that the
subspace need not pass through the origin. This equation will be in general linear form.
o Equation of p dimensional general form:
β0 + β1X1 + β2X2 + … + βpXp = 0
- Linear Separable Hyperplane: Given a set of datapoints with given signed classes and perfectly
linearly separable classes, there will be an infinite number of hyperplanes equations that satisfy
all points being classified correctly. This is demonstrated in the constraints below. If a point is
above the hyperplane it will have a positive value and if it is below the separating hyperplane it
will have a value less than zero. Furthermore, if the class is correctly predicted via the result of
the equation it will share the sign of its respective yi value. Given these two properties of the
hyperplanes we can infer the following constraints.
If yi = 1; β0 + β1X1 + β2X2 + … + βpXp > 0
If yi = -1; β0 + β1X1 + β2X2 + … + βpXp < 0
o We can equivalently rewrite these two inequalities into a single property of the
hyperplane by combining them via a class wise multiplication term. This multiplication
causes no change as we have perfect sign translation without class error.
(Yi) (β0 + β1X1 + β2X2 + … + βpXp) > 0
o The above equation/constraint verifies that all points are properly classified.
o There will be many linear equations that satisfy this equation, but we need to thin this
solution space down. Thus, in order to select the best one, we need to refine the
optimization problem constraints to find the optimal hyperplane that separates the
classes by the maximum amount which we will call margin.
- Margin: In the case of SVM, we define margin as the distance between the classes and their
decision boundary. Consider the previous equation for a hyperplane and consider it has 2
parallel lines equidistant from one another via a distance M. This distance M can be calculated
using the formula for the distance between parallel line:
o M = 2 / (sqrt (∑ ai
2
))
o In this case we are going to expand the margin as much as possible so that there is
maximum separation between classes. This optimization is gone about by minimizing the
denominator of M which is the sum of all coefficients squared. By minimizing the sum of
coefficients, we can maximize the distance between classes while our previous
constraint continues to enforce that all classes are still correctly classified. This will yield
a maximum margin classifier.
- Maximal Margin Classifier: The hyperplane that optimal separates the points into the correct
classes with the greatest margin between the decision boundary:
o Maximize: Margin~ M ~ 2 / (sqrt (∑ ai
2
))
o By Minimizing: ∑ ai
2
o Or by setting a constraint: ∑ ai
2
= 1
o Constrained by: (Yi) (β0 + β1X1 + β2X2 + … + βpXp) ≥ M
o Collectively, this optimization problem lays out that all points be classified correctly with
enough distance from misclassification as specified by the margin amount that satisfies
the inequality relative to its maximized magnitude.
o The points that lie upon the margin equations are support vectors and are equal to the
margin that has been maximized.
- Support Vector Machine: In this variant of a maximal margin classifier, we face a dataset with
non-linearly separable classes. Due to this fact we must allow violations of both the response
and the margin. We assign a cost value to each type of error and optimize the equation to the
following:
o Minimize: Λ * ∑ max {0, 1 – (∑ aixij + a0) (yi)} + λ ∑ ai
2
o Λ a term multiplied by the classification error (larger if misclassification more costly)
o Λ a term multiplied by the margin magnitude (large if margin violations more costly)
o The first term quantifies the magnitude if any of the classification errors
o The second term quantifies the cost of margin violation via the lambda term
o Thus, a small lambda makes margin violations less impactful leaving more budget for
errors in the classification error term as a margin violation is less costly.
o On the other hand, a large lambda leaves little room for the classification error term and
instead prioritizes maximal margin as a violation is more costly.
o The total error will be equal to C also considered a budget of error.
o In SVM C is our cost tuning parameter that caps the sum of error terms to a desired
budget.
o This concept can be driven beyond linear decision boundaries and into a non-linear
decision boundary which is accomplished via the implementation of kernel functions
which use matrix multiplication operations to expand the given feature space into higher
order dimensions and terms. Examples inc predict will be concentrate
[Show More]