ISYE 6501 WEEK 4 HOMEWORK – SAMPLE SOLUTIONS

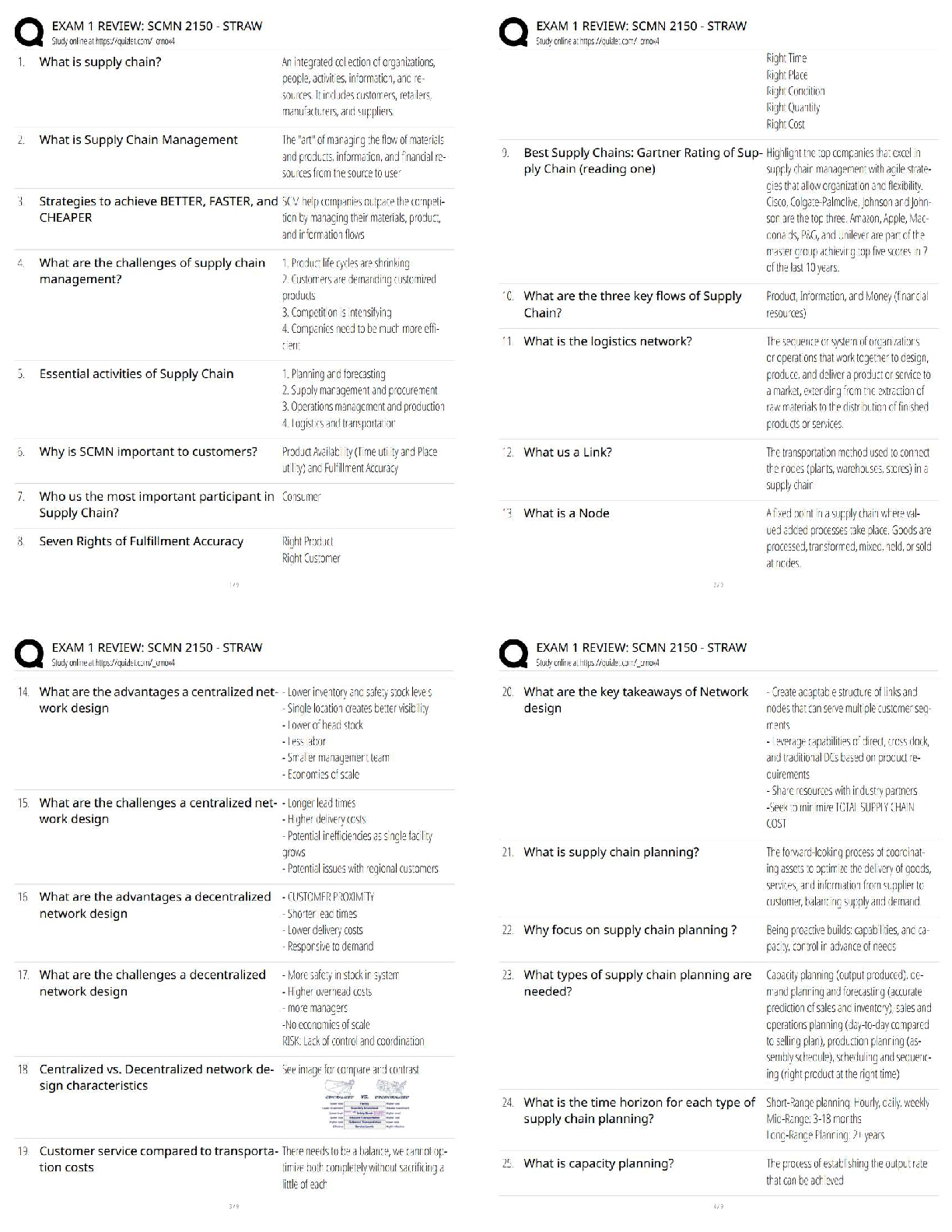
WEEK 4 HOMEWORK – SAMPLE SOLUTIONS IMPORTANT NOTE These homework solutions show multiple approaches and some optional extensions for most of the questions in the assignment. You don’t need to submit all this in your ...

WEEK 4 HOMEWORK – SAMPLE SOLUTIONS IMPORTANT NOTE These homework solutions show multiple approaches and some optional extensions for most of the questions in the assignment. You don’t need to submit all this in your assignments; they’re included here just to help you learn more – because remember, the main goal of the homework assignments, and of the entire course, is to help you learn as much as you can, and develop your analytics skills as much as possible! Question 1 Using the same crime data set as in Homework 3 Question 4, apply Principal Component Analysis and then create a regression model using the first 4 principal components. Specify your new model in terms of the original variables (not the principal components), and compare its quality to that of your solution to Homework 3 Question 4. You can use the R function prcomp for PCA. (Note that to first scale the data, you can include scale. = TRUE to scale as part of the PCA function.) Here’s one possible solution. Please note that a good solution doesn’t have to try all of the possibilities in the code; they’re shown to help you learn, but they’re not necessary. The file HW4-Q1.R shows how to calculate the principal components, run a regression, and find the resulting coefficients in terms of the original variables. The model using the first four principal components is the following: Crime ~ 905 – 21.3M + 10.2So + 14.4Ed + 63.5Po1 + 64.6Po2 – 14LF – 24.4MF + 39.8Pop + 15.4NW – 27.2U1 + 1.43U2 + 38.6Wealth – 27.5Ineq + 3.3Prob – 6.61Time Its R2 is just 0.309, much lower than the 0.803 found by the regression model found in the previous homework. But, remember that cross-validation showed a lot of overfitting in the previous homework. The R code shows the results using the first k principal components, for k=1..15: Model R-squared on training data Cross-validation R-squared Top 1 principal component 0.17 0.07 Top 2 principal components 0.26 0.09 Top 3 principal components 0.27 0.07 Top 4 principal components 0.31 0.11 Top 5 principal components 0.65 0.49 Top 6 principal components 0.66 0.46 Top 7 principal components 0.69 0.46 Top 8 principal components 0.69 0.37 Top 9 principal components 0.69 0.33 Top 10 principal components 0.70 0.30 Top 11 principal components 0.70 0.19 Top 12 principal components 0.77 0.39 Top 13 principal components 0.77 0.39 Top 14 principal components 0.79 0.47 Top 15 principal components 0.80 0.41 All original variables [from HW3] 0.80 0.41 From the table above, it seems clear that there’s still over-fitting (not surprising with so few data points for the number of factors, as we saw in HW3). And it seems clear that adding the 5th principal component is important. Question 2 Using the same crime data set as in Homework 3 Question 4, find the best model you can using (a) a regression tree model, and (b) a random forest model. In R, you can use the tree package or the rpart package, and the randomForest package. For each model, describe one or two qualitative takeaways you get from analyzing the results (i.e., don’t just stop when you have a good model, but interpret it too). (a) Regression Tree Here’s one possible solution. Please note that a good solution doesn’t have to try all of the possibilities in the code; they’re shown to help you learn, but they’re not necessary. The file HW4-Q2a.R shows how to build the regression tree. It shows two different approaches: one using part of the data for training and part for testing, and one uses all of the data for training (because we have only 47 data points). A visualization of one of the trees is below. The tree in the figure (sometimes called a “dendro gram”) shows that four factors are used in branching: Po1, Pop, NW, and LF. Notice that Pop is used in two places in the tree. Also notice that following the rightmost branches down the tree, Po1 is used twice in the branching: once at the top, and then again lower down. | Po1 < 7.65 Pop < 22.5 LF < 0.5675 NW < 7.65 Pop < 21.5 Po1 < 9.65 500 700 800 1000 700 1000 2000 It turns out that the model is overfit (see the R file). The R file shows a lot more possible models, including pruning to smaller trees, using regressions for each leaf instead of averages, etc. The models show that Po1 is the primary branching factor, and when Po1 < 7.65, we can build a regression model with PCA that can account for about 30% of the variability. But for Po1 > 7.65, we don’t have a good linear regression model; none of the factors are significant. This shows that we would need to either try other types of models, or find new explanatory factors.