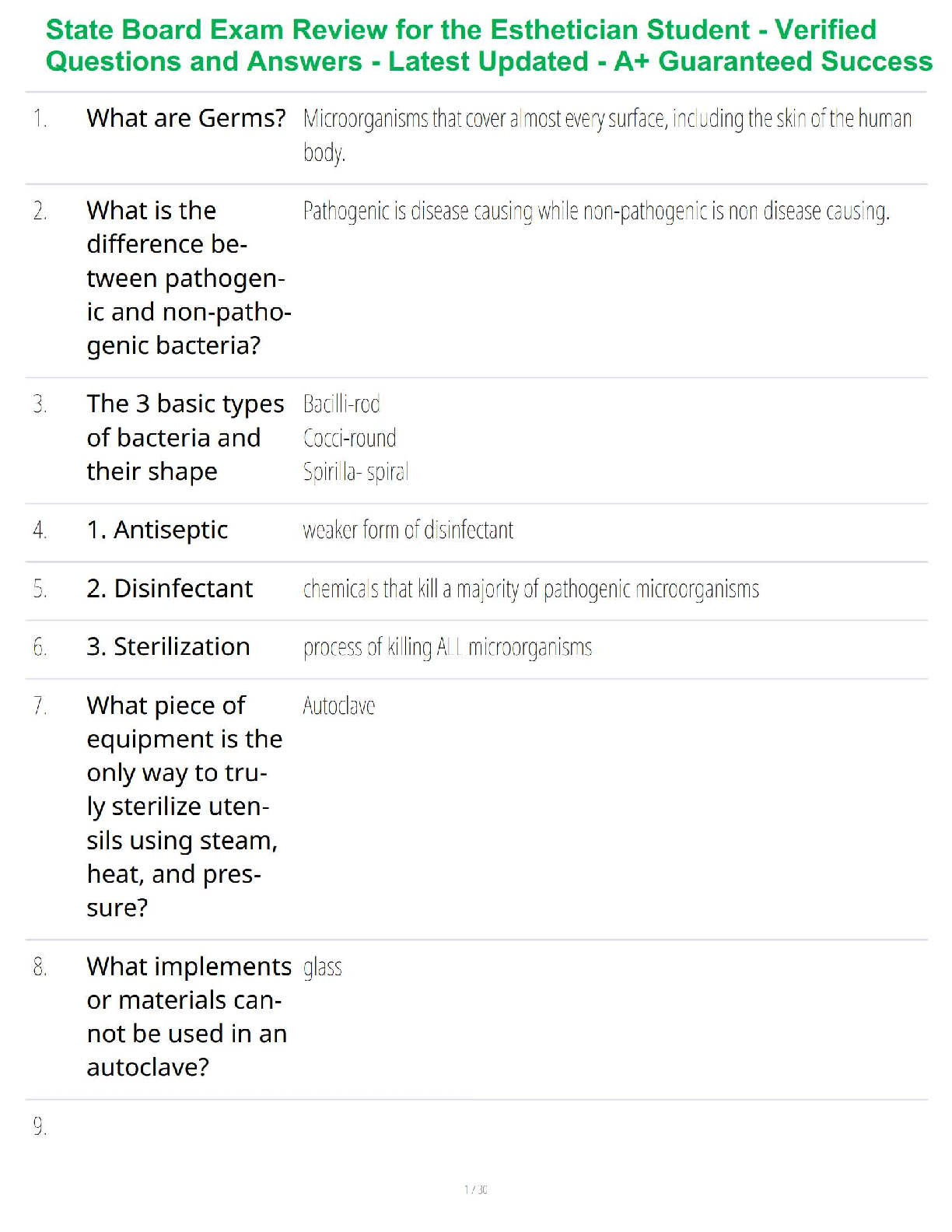
WEEK 11 HOMEWORK – SAMPLE SOLUTIONS

WEEK 11 HOMEWORK – SAMPLE SOLUTIONS IMPORTANT NOTE These homework solutions show multiple approaches and some optional extensions for most of the questions in the assignment. You don’t need to submit all this in you ...

WEEK 11 HOMEWORK – SAMPLE SOLUTIONS IMPORTANT NOTE These homework solutions show multiple approaches and some optional extensions for most of the questions in the assignment. You don’t need to submit all this in your assignments; they’re included here just to help you learn more – because remember, the main goal of the homework assignments, and of the entire course, is to help you learn as much as you can, and develop your analytics skills as much as possible! Question 1 Describe a situation or problem from your job, everyday life, current events, etc., for which optimization would be appropriate. What data would you need? Some (perhaps overzealous!) baseball fans have tried to drive around the country to see a baseball game at each of the 30 Major League stadiums, and then return home, in the shortest number of days. This can be modeled using optimization: minimize the number of days it takes, subject to the constraints that a game is seen at each stadium, and the planned sequence of games is possible given the driving times and game schedules. The necessary data would include the Major League schedule (which stadiums have games scheduled on each day, and what time they’re scheduled for), and how long it takes to drive between each pair of stadiums. Question 2 In the videos, we saw the “diet problem”. (The diet problem is one of the first large-scale optimization problems to be studied in practice. Back in the 1930’s and 40’s, the Army wanted to meet the nutritional requirements of its soldiers while minimizing the cost.) In this homework you get to solve a diet problem with real data. The data is given in the file diet.xls. Here’s one possible solution. Please note that a good solution doesn’t have to try all of the possibilities in the code; they’re shown to help you learn, but they’re not necessary. 1. Formulate an optimization model (a linear program) to find the cheapest diet that satisfies the maximum and minimum daily nutrition constraints, and solve it using PuLP. Turn in your code and the solution. (The optimal solution should be a diet of air-popped popcorn, poached eggs, oranges, raw iceberg lettuce, raw celery, and frozen broccoli. 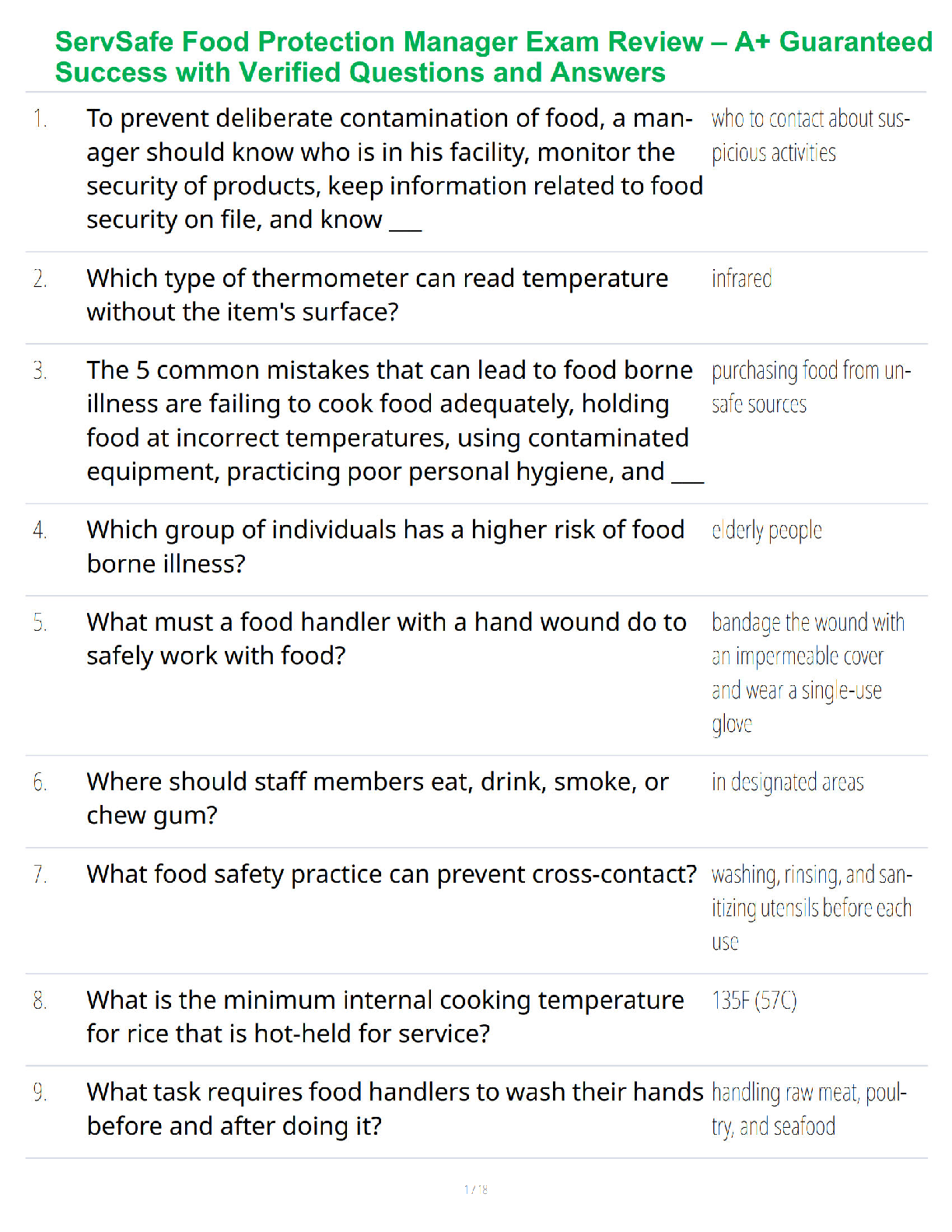UGH!) Algebraically, here’s what the model looks like: Data ???? = cost per unit of food ?? ?????? = amount of nutrient ?? per unit of food ?? ???? = minimum amount of nutrient ?? required ???? = maximum amount of nutrient ?? required Variables ???? = amount of food ?? eaten Objective Minimize ∑?? ???????? (minimize total cost) Constraints ∑?? ?????????? ≥ ???? for each nutrient ?? (take in at least minimum amount of each nutrient) ∑?? ?????????? ≤ ???? for each nutrient ?? (take in no more than max amount of each nutrient) ???? ≥ 0 for each food ?? (can’t eat negative amounts) The file HW11-Q2-1-EachNutrientSeparate-fall.py shows one way to solve the problem. This file deals with each nutrient separately, to show what the problem looks like. However, an easier way to do it is shown in file HW11-Q2-1-SimplerFormat-fall.py, where data is read and constraints are written in a loop, so individual nutrients don’t need to each be written out. This will come in handy when there are more constraints (like the optional part below). However you set up the problem, here’s the optimal solution: ## ---------The solution to the diet problem is---------- ## 52.64371 units of Celery,_Raw ## 0.25960653 units of Frozen_Broccoli ## 63.988506 units of Lettuce,Iceberg,Raw ## 2.2929389 units of Oranges ## 0.14184397 units of Poached_Eggs ## 13.869322 units of Popcorn,Air_Popped ## ## Total cost of food = $4.34 It’s a pretty cheap daily diet, but not one that looks particularly delicious! 2. Please add to your model the following constraints (which might require adding more variables) and solve the new model: a. If a food is selected, then a minimum of 1/10 serving must be chosen. (Hint: now you will need two variables for each food i: whether it is chosen, and how much is part of the diet. You’ll also need to write a constraint to link them.)