GMAT 2021/2022 Questions Answers

Document Content and Description Below

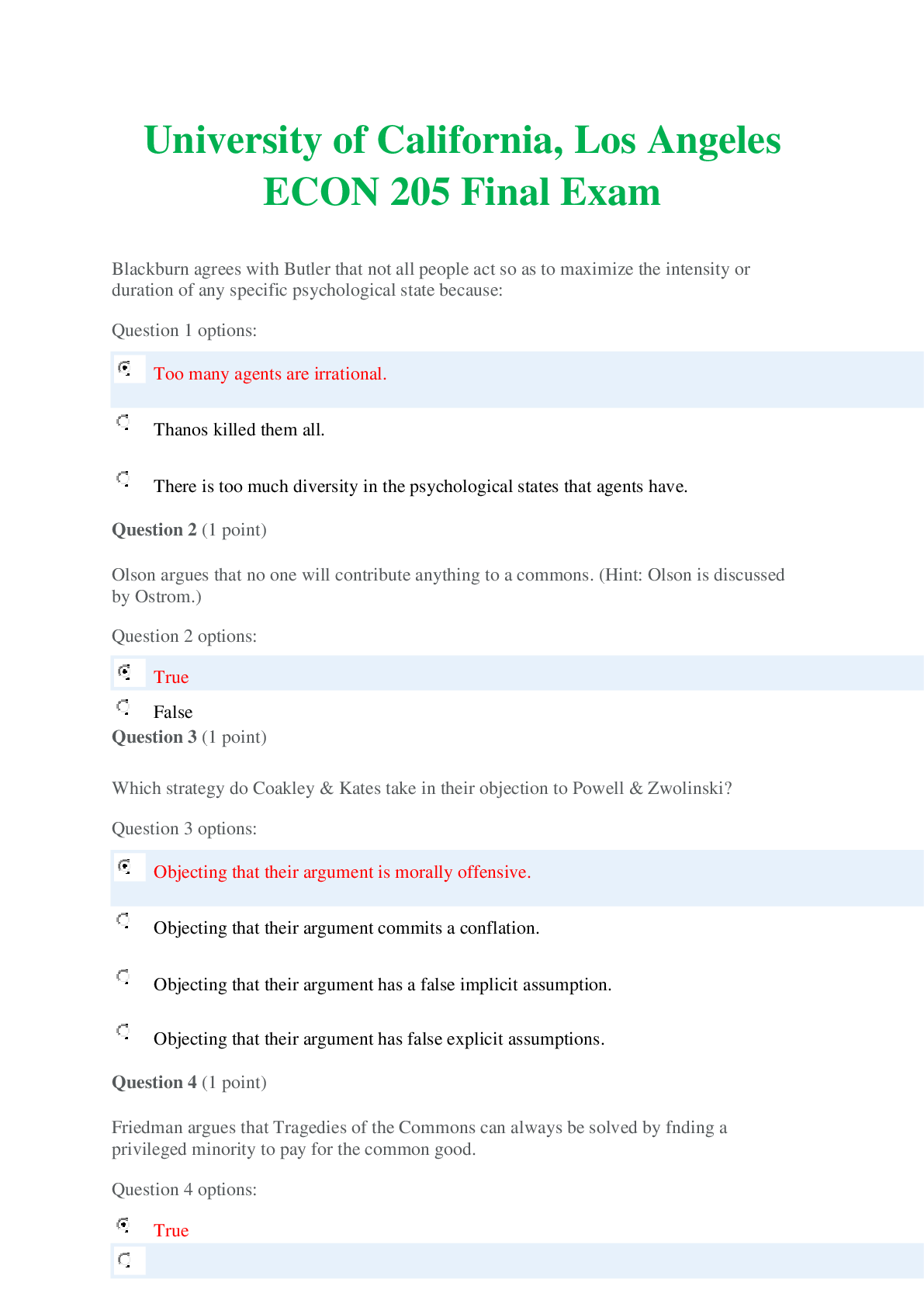
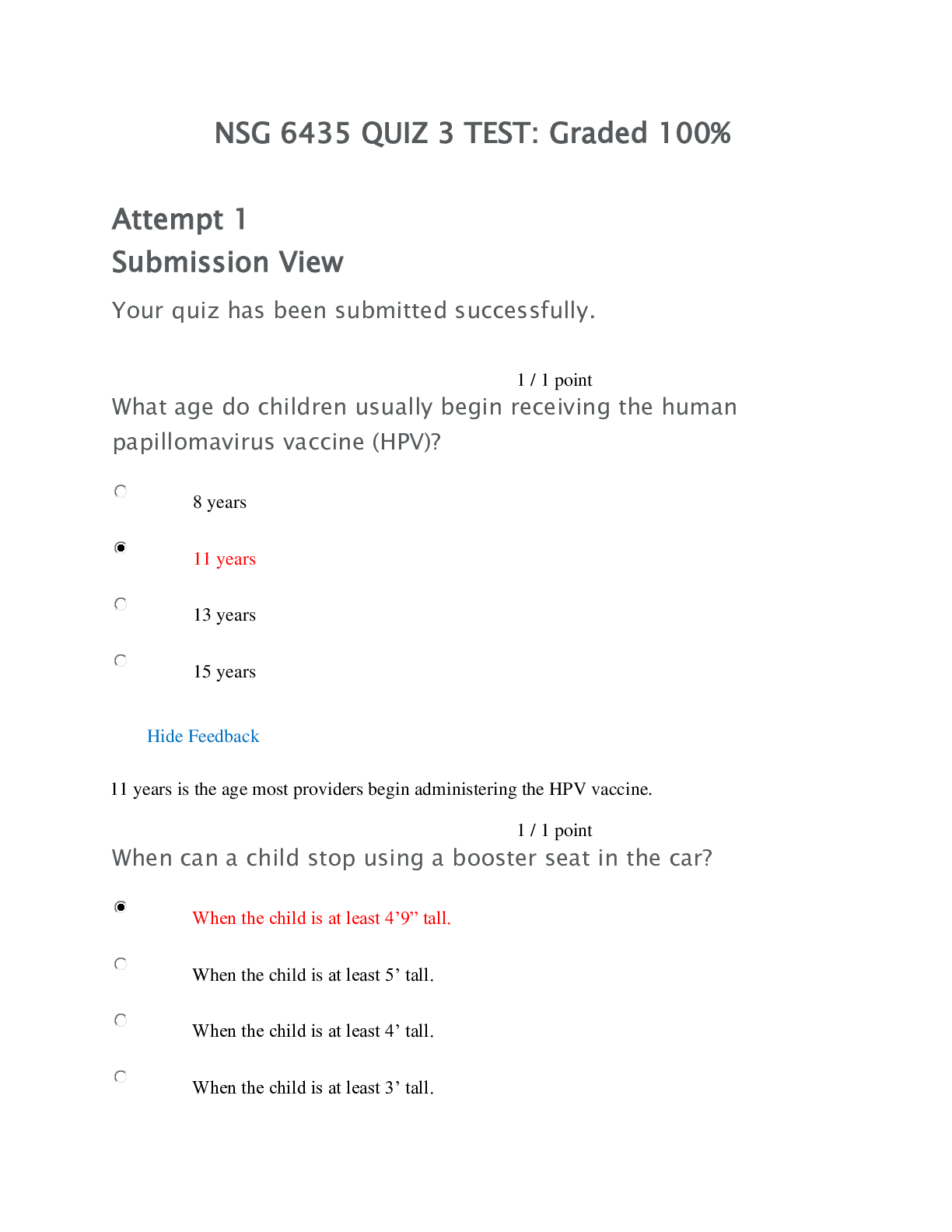
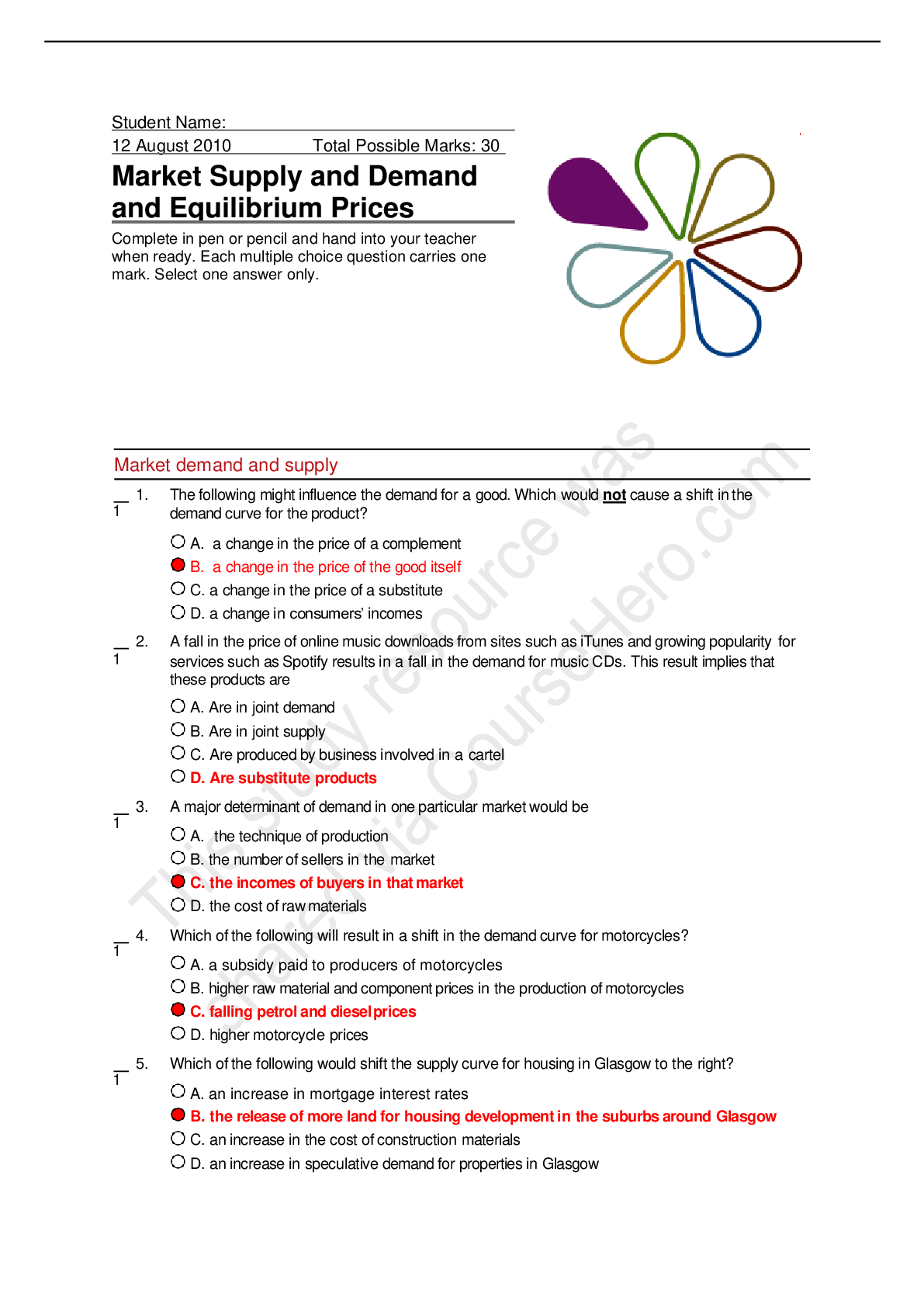
multiplication rules for odd and even numbers even x even = even even x odd = even odd x odd = odd addition rules for odd and even numbers even + even = even even + odd = odd odd + odd = ev... en how many data sufficiency problems are there? 15 how many problem solving questions are there? 22 Area = ? Length X Width What is the Kaplan method for problem solving? 1. Analyze the question 2. State the task 3. Approach strategically 4. Confirm your answer list the prime numbers to 50 2, 3, 5, 7, 11, 13, 17, 19, 29, 31, 37, 41, 43, 47 (x+y)(x-y) x² - y² (x^a)^b x^ab x^a x x^b x^(a+b) 1/9 (what's the decimal?) 0.11111 1/7 (what's the decimal?) 0.1428 how do you solve an equation in absolute signs? e.g. |4x - 2| = 10 (4x - 2) = 10 AND (4x - 2) = -10 how do you solve an inequality in absolute signs? e.g. |4x - 2| < 10 (4x - 2) < 10 AND (4x - 2) > -10 divisibility test for 7 separate the units digits from the rest of the number, then multiply that unit digit by 2. subtract from what's left of the original number. if the result is a multiple of 7 or 0, the original number is a multiple of 7. a^b x a^c = a^(b+c) a^b / a^c = a^(b-c) a^(-b) = 1 / (a^b) raising a positive fraction less than 1 to a positive exponent greater than 1 results in a ____ value. the higher the exponent, the ___ the result. smaller value, smaller when a negative number is raised to an even exponent, the result is... positive when a negative number is raised to an odd exponent, the result is negative √ab = ? (√a) x (√b) √(a/b) = (√a) / (√b) √(a+b) ≠ (√a) + (√b) √(a−b) ≠ (√a) - (√b) (√a)² = a √a a^(1/2) Even x any number = Even Even ± Odd = Odd Odd ± Odd = Even Even ± Even = Even Even^(positive integer) = Even odd^(positive integer) = odd define a prime number positive integer greater than 1 that is divisible only by 1 and itself if given a rectangle's area and perimeter... find area's factors and see which ones add up to perimeter ÷ 2 integer is ... positive whole numbers, zero, and negative whole numbers the remainder of n / 3 is 1. what does this imply? n = 3x +1 or (n-1) is a multiple of 3 perfect square? is an integer which is the square of an integer what and how many are the prime factors of a prime number? itself. there is only 1 prime factor as 1 is not a prime number. name all known right triangles and their dimensions 3:4:5 (and proportional) 5:12:13 (and proportional) 7:24:25 8:15:17 9:40:41 isosceles right triangle: x:x:x√2 30-60 right triangle: x:x√3:2x speed = D/T Distance (how it relates to speed) = (S)(T) average speed = total distance / total time multi part journeys involving speeds: what strategy should be used? DTS table combined work question (same task performed by several people): what strategy should be used? rate = (number of tasks) / (time to complete tasks) 2 workers: T = (AB)/(A+B) combined work question formulas: more than 2 workers? 1 / T = 1 / A + 1 / B + 1 / C .... strategy for questions involving same route traveled by 2 people... 1) when leaving at different times 2) in opposite direction 3) in same direction 1) recalculate distance from the point at which both people are moving 2) sum of speeds = Distance (from time when both people are moving)/ (Time); Time = (Distance)/(Sum of speeds) 3) Difference of speeds = (Distance/Time) Overlapping sets questions strategy? (1) Table (2) Venn diagram if more than 2 sets (3) formula: Total = Group 1 + Group 2 - Both + Neither Polygons with n sides sum of interior angles = ? (n-2)(180°) Parallelogram area and properties: Base x Height opposite sides are equal opposite angles are equal diagonals bisect trapezoid area? [(1/2)(sum of bases)](height) a line with exactly 1 point in common with a circle is ______ and is ____ with reference to the radius tangent to the circle and is perpendicular to the radius if a triangle is incribed in a circle so that on of its sides is a diameter of the circle, then the triangle is: a right triangle To calculate number of arrangements where some of the elements are indistinguishable e.g.(1) possible 7-digit codes out of a choice of 3A's, 2B's, 1C and 1D e.g.(2) probability of 2 heads in a series of 3 coin tosses (total number of arrangements) / (Factorial of number of indistinguishable elements) e.g.(1) 3A's and 2B's are indistinguishable hence 7! / (3! x 2!) e.g.(2) a specific combination has the probability of 0.5 x 0.5 x 0.5 = 0.125 (or 1/8). Multiply this by number of ways of arranging HHT, which is 3! / (2! x 1!) = 3. Answer is 0.125 x 3 = 0.375 Probability of events A and B P(A) x P(B) Probability of event A or event B (assuming A and B are independent) P(A) + P(B) - P(A and B) P(A) + P(B) - P(A) x P(B) combination formula: n! / [k! (n - k)!] (n + k - 1)!/ r!(n-1)! (without repetition) what does combination formula give? number of UNORDERED subgroups of k items that can be selected from a group of n different items permutation formula: n! / (n - k)! where n is the number of things to choose from, and we choose k of them (no repetition, order matters) what does the permutation formula give? number of ORDERED subgroups of k items that can be selected from a group of n different items Strategy if asked for different combinations/permutations of 2 distinct groups: separate calculation of combination/permutation by group, then multiply the 2 results number of terms in a sequence of consecutive integers = largest - smallest + 1 sum of sequence of consecutive or evenly spaced integers multiply the avg of largest and smallest term by the number of terms number of terms in a sequence of evenly spaced integers e.g. by space of 3 (largest - smallest)/(3+1) 166 foot sidewalk, plant trees evenly spaced by 14 feet, each tree takes up 1 foot. what is the max number of trees? 166/(14+1) = 11 with a remainder of 1, which means there is 1 more foot left for another tree, hence 12 trees what is the mode of a set of data? number appearing the most standard deviation = square root of average squared difference with mean what is the root of an equation? solution if a number N has to be a multiple of one of the answers and we know N is a multiple of x and y, then what should you look for? look for the least common multiple of x and y. LCM is a multiple of the answer Strategy if asked for number of outcomes using combination and then imposing a rule. e.g. choose 4 out of a set of 8 people BUT at least 1 of Jane and Austin needs to be in the 4 chosen First calculate total outcomes using combination rule, then deduct the number of outcomes where the rule does not apply. ⁸C₄ - ⁶C₄ = 70 - 15 = 55 Strategy for a code which needs to contain a combination of certain specific numbers as well as indistinguishable numbers e.g. 6-digit code where 1 digit is a 3, 2 digits are 4, 1 digit is 5 AND the each other digit is 7 or 8 for combination of specific numbers, think of (1) ways in which the given numbers can be ordered (e.g. for 7 and 8, this would be 7:8, 7:7, 8:8, 8:7) and then the ways in which they can be put into the required spaces (e.g. ⁶C₂ or 15). Multiply the 2. For the other numbers, use the factorial divided by factorials of duplicates e.g. 4 remaining numbers to place where 2 numbers are duplicates means 4! / 2!. Multiple 2 results. (x^z)(y^z) (xy)^z rule for divisibility by 4 number formed by the last two digits is divisible by 4 (including 00) 2 is the only ___ prime number even if a and b are integers greater than 1, their product cannot be ___. prime in a mixed fraction, what is the same as the numerator? the remainder 0 is an ___ integer. even slope of 2 point in a coordinate plane = rise/run = (y₂ - y₁) / (x₂ - x₁) which only combinations of 2 terms yield odd numbers? odd x odd odd + even 1 foot = ? inches 12 1 yard = ? feet 3 1 mile = ? feet 5,280 FAST strategy for system of 2 equations, 2 variables COMBINATION: add or subtract one equation from the other to cancel out one of the variables divisibility test by 6... both divisible by 2 and by 3 divisibility test by 8... number formed by the last 3 digits is divisible by 8, including 000 divisibility test by 9... sum of the digits is divisible by 9 is zero positive or negative? neither one nor the other how do you solve x + 6 < |x| ? if x is positive: x+6< x (not possible) if x is ): 6<0 (not possible) if x is negative: x+6<-x (x<-3) if a, b, and c are different positive prime numbers how many distinct positive factors does the product abc have? 8 (1, abc, a, b, c, ab, bc, ac) if given a ratio for item x to item y as a:b and then a separate ratio for item y to item z as c:d then what is ratio of item x to item z? ac:bd can you derive an overall average from weighted averages? yes what is the sum of differences between each term and the average? 0 what is the exterior angle theorem for triangles? exterior angle at a vertex of a triangle equals the sum of the sizes of the interior angles at the other two vertices of the triangle ⁶C₃ = ? 20 if the order doesn't matter, it is a _____. if the order does matter, it is a ____. combination, permutation 4! = 7! = 1! = 0! = 4! = 4 x 3 x 2 x 1 = 24 7! = 7 x 6 x 5 x 4 x 3 x 2 x 1 = 5040 1! = 1 0! = 1 6 children (ABCDEF) are to be seated on a row of 6 chairs. A and E cannot sit next to each other. How many different arrangements? (1) calculate cases where A and B do sit together. AE can be arranged in 10 different ways (AE or EA in 5 different ways) the rest of the children can sit in 4! ways (2) total number of arrangements: 6! = 720 answer is (2) - (1) 5 distinguishable wires. 2 cable wires and 3 phone wires. How many combinations of 3 wires with at least 1 of the wires being cable? (1) total combos: ⁵C₃ (2) number of combos of 3 wires with 3 phone wires: 1 (as this is combination and not permutation) answer is (1) - (2) How to convert 25⁷ x 4⁸ into the format A x 10^b? 5¹⁴ x 2¹⁶ = 2² x 2¹⁴ x 5¹⁴ Probability of A is p and probability of B is q. what is the probability of one of A or B occurring? P(A and not B) + P(B and not A) = p(1-q) + q(1-p) = p + q - 2pq DistanceTimeSpeed problem with not enough data PICK NUMBERS 3 set Venn diagram problems: * if given intersection of AB, BC, AC * if given number of people choosing exactly 2 items * if given number of pile choosing at least 2 items Total = N(A) + N(B) + N(C) - N(A n B) - N(A n C) - N(C n B) + N(A n B n C) Total = N(A) + N(B) + N(C) - (N(choose exactly two items)) - 2N(choose all three items) Total = N(A) + N(B) + N(C) - (N(choose at least two items)) - N(choose all three items) An equilateral triangle can be divided into 2 ..... triangles 3/60 right when picking numbers for an odd number, try __ and __ first. 1 and 3 in any set of four consecutive integers, exactly one will be a multiple of... 4 Strategy for Question stem asking for whether 2 variables m and n are consecutive set up as m=n+1 and m=n-1 and try these out in statements a figure is inscribed within a circle if... all vertices are on the circle's circumference Factors of a positive integer are... They are sometimes called... numbers that divide evenly into a given number. Divisors. divisibility test by 12... multiple of 3 (digits add up to multiple of 3) and of 4 (number formed by last 2 digits is divisible by 4) there are finite number of ___ and a multitude of ____. factors multiples 0 raised to any power other than 0, equals 0 1 raised to any power is 1 (X²Y⁴)³ =? X⁶Y¹² 0 raised to the power of 0 is undefined the sq root of a fraction will be larger/smaller than the fraction itself larger [Show More]

Last updated: 2 years ago

Preview 1 out of 13 pages