Questions and Answers > MATH 451 Decision Trees for Multistage Decision Making

Document Content and Description Below

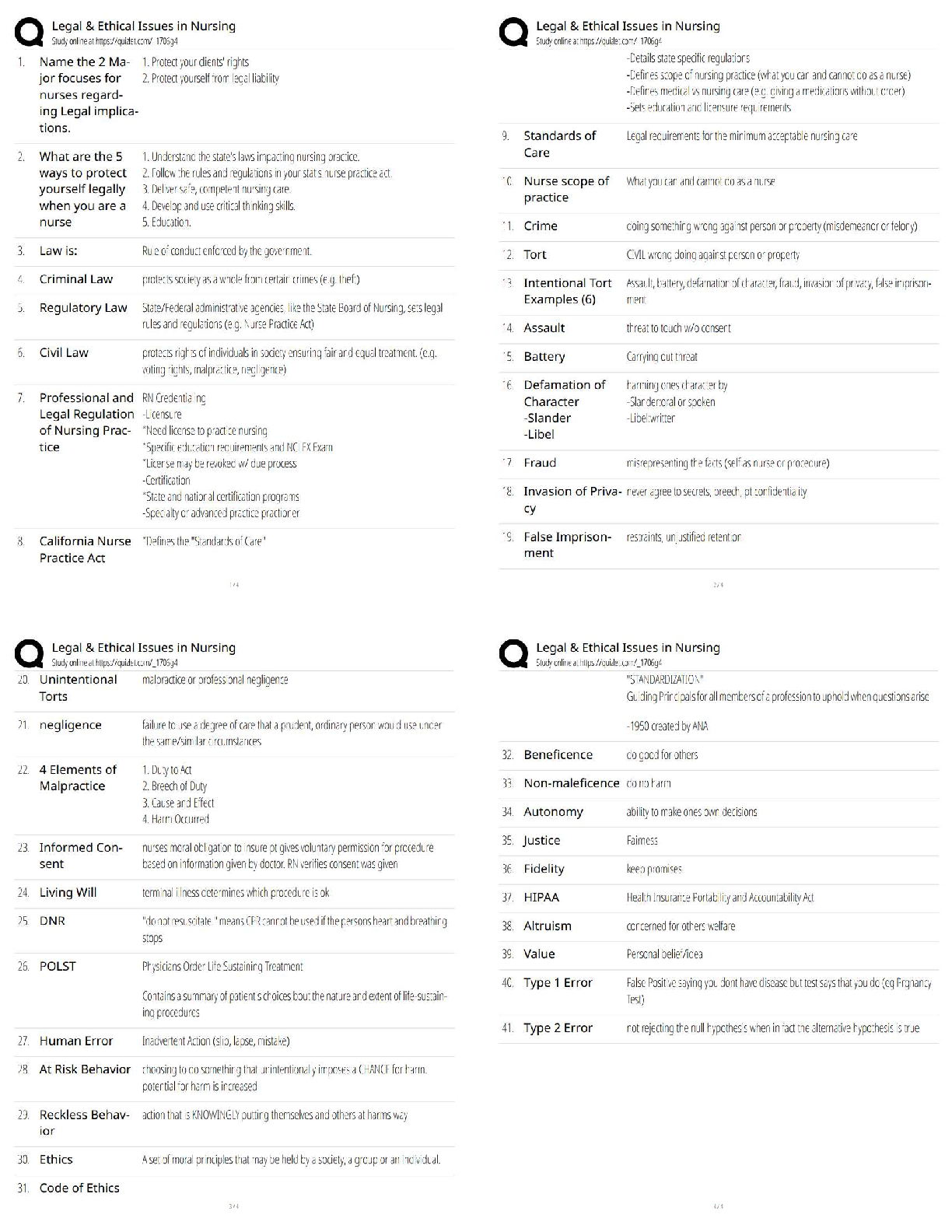
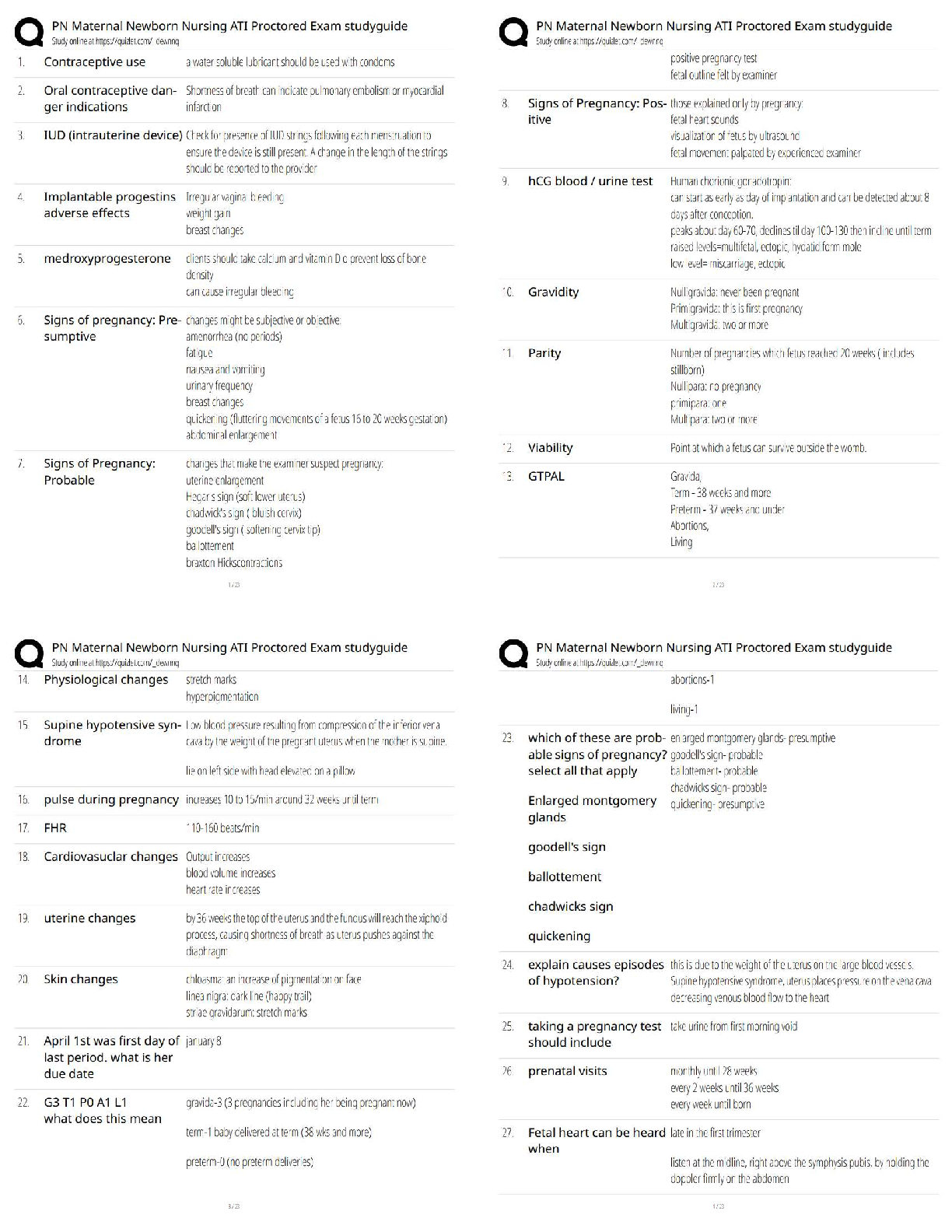
MATH 451 Decision Trees for Multistage Decision Making Introduction A decision tree can be used to represent a decision table. A decision tree looks like a network with nodes and arcs. A decision ... tree presents the decision alternatives and outcomes in a sequential manner. Learning Materials How a Decision Tree Works A decision tree can replace the decision table for many decision-making applications. Decision trees have decision nodes and decision outcomes. A decision node has several arcs connected to it. The arcs originating from that node denote all decision alternatives available to the decision maker at that node. Arcs originating from an outcome node denote all outcomes that could happen at that node. Most of trees start from a decision node. At each outcome node, you will compute the expected payoff using the probabilities of all possible outcomes at that node and the payoffs related with these outcomes. At each decision node, you pick the alternative that produces the better expected payoff. Original Scenario Consider a company’s outcome for four different decision-making options. The following table shows the payoff of each alternative. Produce a Decision Tree Use a treeplan.xla program to produce the tree shown in Figures 1 through 3. Figure 1 Click here for an enlarged image. Figure 2 Click here for an enlarged image. Figure 3 Click here for enlarged image. Probabilities In the above example, you are considering using a survey company that offers some sample information which may not be very accurate for better decision making for a value of $5,000. They have provided the following probabilities for all alternatives you consider here: Consider the following decision tree fragment: Can this be reduced to one decision node? For each decision, can it be further reduced to one outcome node? What does this look like? Yes, each possible path through the tree represents a decision and outcome pair. No, each possible path through the tree represents an outcome but not a decision. Yes. However, changing the problem reduces the second decision (e.g., in the fragment above, eliminating node 2 and beyond). No. For example, the outcome at node A must be known before a decision is made at node 2. A company has outcomes for four different decision-making options they have. The following table shows the payoff of each alternative. Question 2 What are the branches for the decision node? Moderate demand Larger plant, median plant, small plant, and no plant Low demand High demand What type of problem is a decision table mostly convenient for? No stage problem Two stages problem Multistage problem One stage problem The correct answer is: Start the program Begin a new tree Add nodes and branches Change the titles, probabilities, and payoffs Identify the best decision Make minor formatting changes What has a decision maker access to at an outcome node? Some of the outcomes that could happen All of the decision alternatives All the outcomes that could happen Some of the decision alternatives A company has outcomes for four different decision-making options they have. The following table shows the payoff of each alternative. Question 1 How much is the expected monetary value (EMV) at the larger plant with no survey? $0 $117,310 $84,000 $119,310 The Absolute (ABS) part of the formula verifies that the sum of all probabilities at a given outcome node is __________. equal to 1 with a tolerance of 0.00001 less than 1 equal to 1 with absolutely no tolerance greater than 1 Which of the following can be said about the probabilities in the given tree? prob c3 × prob b2 × prob a1 = 1 prob a1 + prob a2 + prob a3 = 1 prob a1 might be different from prob a2 prob a3 + prob c1 = 1 – prob b3 A company has outcomes for four different decision-making options they have. The following table shows the payoff of each alternative. Question 4 What is the value of expected monetary value (EMV)? Larger plant High demand, moderate demand, and low demand Small plant Median plant A company has outcomes for four different decision-making options they have. The following table shows the payoff of each alternative. Question 6 How much is the expected monetary value (EMV) at the larger plant with the positive survey? $119,310 $84,000 $0 $40,810 Suppose that you face two choices. If you pick choice 1, then outcome A will bring a profit of 100, while outcome B will result in a loss of 100. Choice 2 is similar, but outcome A will result in a loss of 100, while outcome B will result in a profit of 100. Not knowing much more, the best that you can do is assign equal probability to outcomes A and B. You find out that Synthetic Surveys, a market research company, can give you better information about the probabilities of the outcomes. Synthetic charges 7 to do the survey, which will provide new probabilities for the outcomes. You expect that the probability estimate for outcome A will either be , where (delta) is a change. Each of these outcomes is equally likely. Which of the following inequalities expresses a condition that the survey is worth it? Suppose that you face two choices. If you pick choice 1, then outcome A will bring a profit of 100, while outcome B will result in a loss of 100. Choice 2 is similar, but outcome A will result in a loss of 100, while outcome B will result in a profit of 100. Not knowing much more, the best that you can do is assign equal probability to outcomes A and B. You find out that Synthetic Surveys, a market research company, can give you better information about the probabilities of the outcomes. Synthetic charges 7 to do the survey, which will provide new probabilities for the outcomes. You expect that the probability estimate for outcome A will either be , where (delta) is a change. Each of these outcomes is equally likely. What value of will make it worthwhile to do the survey? When designing a decision tree, the outcome is independent of the decision. For example, it is assumed that the future demand for a product, the outcome, is independent of whether you build a large factory, a small factory, or no factory at all. You can extend this to imagining that instead of a big environment, which will produce an outcome independent of your actions, your concern is with a competitor that will respond to your actions. This is called game theory. Suppose that you and a competitor each have about 50% of the market per year. You can spend $2,000,000 to reduce your production costs. If your competitor does nothing, this will allow you to wipe your competitor out and corner the market. Your competitor can likewise spend the $2,000,000 to improve its production. The numbers show the result for you and your competitor. For example, 2, -2 means that you get 2 and your competitor loses 2. What does the tree look like? What is the likely outcome? It looks like tree C or D. Both lose 2. It looks like tree A or D. Both gain 2. It looks like tree A or B. Both lose 2. It looks like tree A or D. Both lose 2. The following is a sample decision tree is shown below (Note that the information in parentheses is the probability and payoff for a choice followed by an outcome): Which of the following is true? The expected payoff for option 2 is -20a + 120b + 20c. The expected payoff for choosing option 2 is 20(a + 60b – c). The expected payoff from choosing option 1 is 10(10a + b + c). The expected payoff for option 3 is 30(a + b + 10c). Summary In this section, you considered the treeplan to solve a decision-making problem. The payoff without the survey ($139,000) turned out to be better than utilizing the survey ($137,256). Therefore, you do not hire the survey company. Consider the following decision tree fragment: Can this be reduced to one decision node? For each decision, can it be further reduced to one outcome node? What does this look like? Yes, for each decision at node 1, pick in advance what you will decide after the outcome. In the fragment above, this means that a decision includes the choice at node 1 and node 2. No, each possible path through the tree represents an outcome but not a decision. Yes. However, changing the problem reduces the second decision (e.g., in the fragment above, eliminating node 2 and beyond). No, each possible path through the tree represents a decision but not an outcome. Suppose that you face a choice of two options. If you pick choice 1, then outcome A will bring a profit of 200, while outcome B will result in a loss of 100. Choice 2 is different: outcome A will cause a loss of 100, while outcome B will give a profit of 100. Your best estimate of the situation is that outcome A has a 40% probability of occurring. You find out that Synthetic Surveys, a market research company, can give you better information about the probabilities of the outcomes. Synthetic charges 7 to do the survey, which will provide new probabilities for the outcomes. You expect that the probability estimate for outcome A will either be , where (delta) is a change. Your intuition tells you that decreasing the already lower likelihood of outcome A is twice as likely as increasing it. What value of will make it worthwhile to do the survey? >10% >30% >9.5% >10.5% A company has outcomes for four different decision-making options they have. The following table shows the payoff of each alternative. Question 3 How much is the expected monetary value (EMV) without survey at the first decision point? What is the value of expected monetary value (EMV)? $119,310 $40,810 $82,336 $84,000 What has a decision maker access to at a decision node? Neither to any of the decision alternatives nor the outcomes All the outcomes that could happen All the decision alternatives to consider selecting only anyone of them All the decision alternatives and outcomes When working with decision trees, a decision node is shown as a little box, and the outcome node is shown as a little circle. The following is a decision tree with some information missing: Which of the following statements is correct? Detailed descriptions of the outcomes are needed in the tree. The decision maker has 3 choices: choice 1, choice 2, and choice 3. There are 3 outcomes being considered: 1, 2, and 3. The decision make has 3 choices: choice A, choice B and choice C. Suppose that you face two choices. If you pick choice 1, then outcome A will bring a profit of 100, while outcome B will result in a loss of 100. Choice 2 is similar, but outcome A will result in a loss of 100, while outcome B will result in a profit of 100. Not knowing much more, the best that you can do is assign equal probability to outcomes A and B. You find out that Synthetic Surveys, a market research company, can give you better information about the probabilities of the outcomes. Synthetic charges 7 to do the survey, which will provide new probabilities for the outcomes. You expect that the probability estimate for outcome A will either be , where (delta) is a change. Each of these outcomes is equally likely. What value of will make it worthwhile to do the survey? What has a decision maker access to at an outcome node? Some of the outcomes that could happen All of the decision alternatives Some of the decision alternatives All the outcomes that could happen Suppose that you face a choice of two options. If you pick choice 1, then outcome A will bring a profit of 100, while outcome B will result in a loss of 100. Choice 2 is similar, but outcome A will result in a loss of 100 while outcome B will result in a profit of 100. Not knowing much more, the best that you can do is assign equal probability to outcomes A and B. You find out that Synthetic Surveys, a market research company, can give you better information about the probabilities of the outcomes. Synthetic charges 7 to do the survey, which will provide new probabilities for the outcomes. You expect that the probability estimate for outcome A will either be , where (delta) is a change. Each of these outcomes is equally likely. How many decision nodes does your tree have? 3 5 4 2 What payoffs value does the tree assign to a newly created arc? There is no value associated for any arc 1 Values given by the problem 0 Which of the following can be said about the probabilities in the given tree? prob a2 – prob b1 + prob c3 = .5 prob a1 + prob b2 + prob c3 = 1 prob a1 might be different from prob a2 prob a1 + prob a2 + prob a3 = 1 When designing a decision tree, the outcome is independent of the decision. For example, it is assumed that the future demand for a product, the outcome, is independent of whether you build a large factory, a small factory, or no factory at all. You can extend this to imagining that instead of a big environment, which will produce an outcome independent of your actions, your concern is with a competitor that will respond to your actions. This is called game theory. Suppose that you and a competitor each have about 50% of the market per year. You can spend $2,000,000 to reduce your production costs. If your competitor does nothing, this will allow you to wipe your competitor out and corner the market. Your competitor can likewise spend the $2,000,000 to improve its production. The numbers show the result for you and your competitor. For example, 2, -2 means that you get 2 and your competitor loses 2. What does the tree look like? What is the likely outcome? It looks like tree A or D. Both lose 2. It looks like tree A or D. Both gain 2. It looks like tree A or B. Both lose 2. It looks like tree C or D. Both lose 2. What has a decision maker access to at a decision node? Neither to any of the decision alternatives nor the outcomes All the decision alternatives to consider selecting only anyone of them All the outcomes that could happen All the decision alternatives and outcomes A company has outcomes for four different decision-making options they have. The following table shows the payoff of each alternative. Question 5 How much is the expected monetary value (EMV) at the larger plant with no survey? $119,310 $117,310 $0 $84,000 Which of the following can be said about the probabilities in the given tree? prob a1 + prob a2 + prob a3 = 1 prob a2 – prob b1 + prob c3 = .5 prob a1 might be different from prob a2 prob a1 = prob a3 [Show More]

Last updated: 3 years ago

Preview 1 out of 21 pages