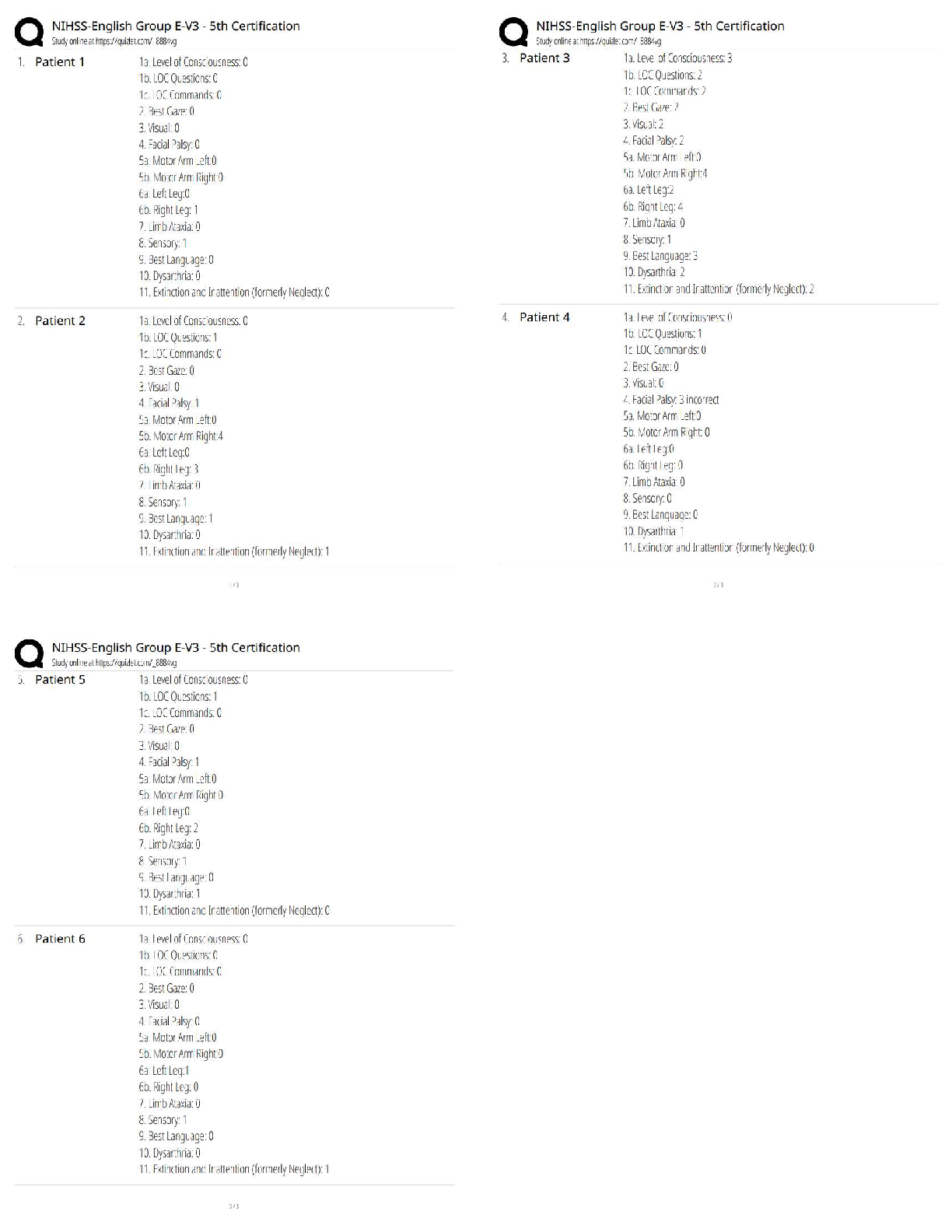
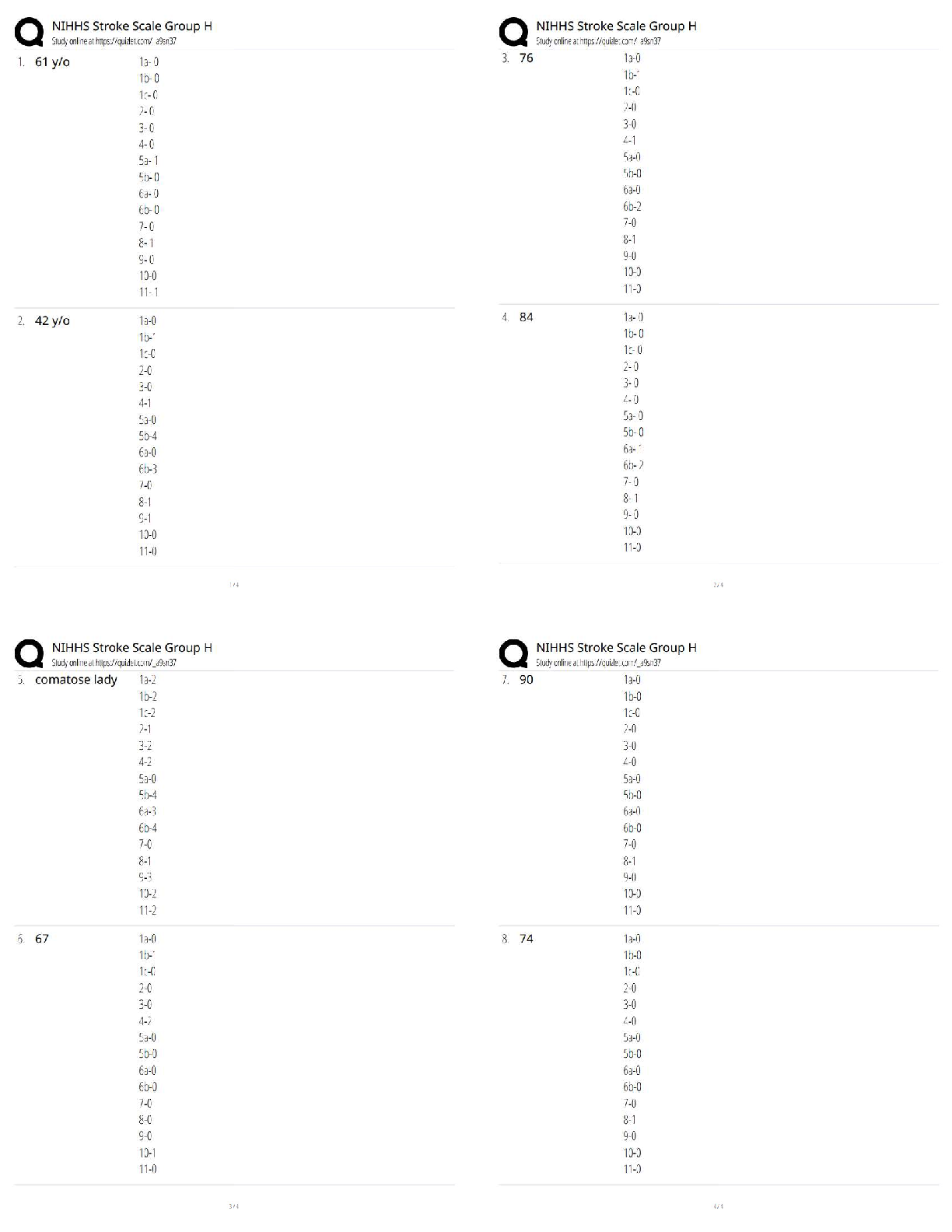
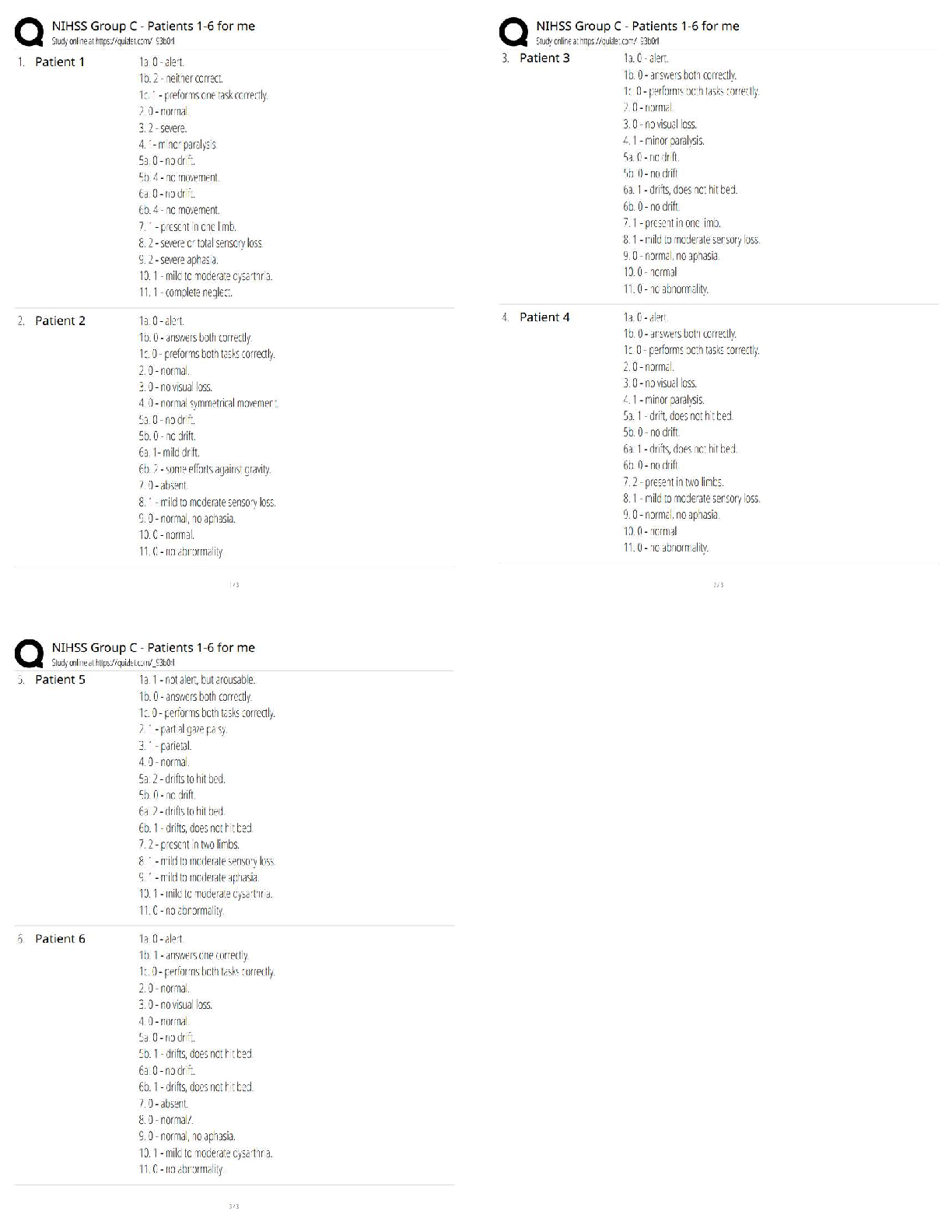
PRECALC 10113.1.3 Final Exam_ Semester Exam (Teacher-Scored)-2. 100% Score

Document Content and Description Below

13.1.3 Final Exam: Semester Exam (Teacher-Scored)z Test Answer the following questions using what you've learned from this unit. Write your responses in the space provided. 1. Consider the right tr ... iangle ABC given below: Part I: Use the sine ratio to find the length of side b to two decimal places. (2 points) 5.07 Part II: Find the length of side a to two decimal places using the method of your choice. (2 points) 10.87 2. Solve the triangle below by finding all missing sides and/or angles. Part I: Use the law of cosines to find the length of side AC. Round your answer to the nearest hundredth. (4 points) 14.79 TFinal-Exam-Semester-Exam-Teacher-Scored-2pdf/Part II: Use the law of sines to find the measure of angle C. (4 points) 39.45 Part III: Find the measure of angle A using any method. (2 points) 30.55 3. Graph the function on the axes below. Part I: What is the amplitude of this function? (2 points) 3 Part II: What is the vertical shift of this function? (2 points) 1 Part III: What is the period of this function? (2 points) pi Part IV: Graph at least two periods of this function. (4 points) 4. An object's motion is described by the equation . The displacement, d, is measured in meters. The time, t, is measured in seconds. Answer the following questions. Part I: What is the object's position (in meters) at t = 0? (4 points) -2 meters Final-Exam-Semester-Exam-Teacher-Scored-2pdf/Part II: What is the object's maximum displacement (in meters) from its t = 0position? (2 points) 3 Part III: How much time (in seconds) is required for one oscillation? (2 points) 1⁄8 sec Part IV: What is the frequency (measured in Hz) of this oscillation? (2 points) 4 Hz 5. Evaluate each of the following. In each case, explain your thinking. a. Part I: What is the value of ? (2 points) Sqrt 3/2 Part II: To solve the problem , find the angle in the interval whose cosine is . (4 points) -pi/2 on unit circle= 3pi/2 or 270 degrees, cosine of that angle 0 b. Part I: Find the measure of the hypotenuse of this triangle. (2 points) 5 Final-Exam-Semester-Exam-Teacher-Scored-2pdf/Part II: Angle is the angle whose tangent is . Find the sine of angle . (2 points) Tan = opposite/adjacent= 4/3 c. Part I: What is the value of ? (2 points) 0 Part II: To solve the problem , find the angle in the interval whose tangent equals 0. (4 points) 0 6. Give the most general solutions to the equation. Part I: Simplify the first expression using the double-angle identity for sine. (2 points) sin(2x)-sin(2x)cos(2x)=0 Part II: Factor the left side of the equation. (2 points) sin(2x)(1-cos(2x))=0 Part III: Solve the factored equation. (6 points) 1-cos(2x)=0->cos(2x)=1 For sin(2x) = 0, this is true for 2x = n(pi) where n = 0, 1, 2, .... x = n(pi/2) For cos(2x) = 1, this is true for 2x = n(pi) where n = 0, 2, 4, .... x = n(pi/2) 7. Given the following identity, :Final-Exam-Semester-Exam-Teacher-Scored-2pdf/Prove the identity by completing the table below, indicating the steps on the left and the reasoning on the right. (12 points) Calculation Reason Given in the problem sec(x)csc(x)[tan(x) + cot(x)] = 2 + tan2(x) + cot2(x) Apply the distributive property sec(x)csc(x)[tan(x)] + sec(x)csc(x)[cot(x)] = 2 + tan2(x) + cot2(x) Apply the definitions of secant, cosecant, tangent, and cotangent sec2(x) + csc2(x) = 2 + tan2(x) + cot2(x) Simplify the expressions sec2(x) + csc2(x) = 1 + 1 + tan2(x) + cot2(x) Apply the definitions of secant and cosecant sec2(x) + csc2(x) = 1 + tan2(x) + 1 + cot2(x) Apply the Pythagorean identities sec2(x) + csc2(x) = sec2(x) + csc2(x) Simplify the expressions Final-Exam-Semester-Exam-Teacher-Scored-2pdf/8. Use the sum identity for tangent to find the exact value of . Part I: Find two common angles that sum to . (2 points) 1/sqrt2 ,tan(x)=1 and -sqrt3/2, tan(x)=1/sqrt Part II: Evaluate the expression using the sum identity for tangent. (4 points) 2+sqrt 3 9. Consider the vector . Part I: Use the dot product to find the angle (in degrees) between and the vector (1,0). (4 points) -6 angle=cos^-1 (sqrt(6^2) / ( (sqrt(6^2 + 13^2) x sqrt(1^2) ) Part II: Writev in the form . Express the angle in degrees. (4 points) v= (5sqrt10cos(112.3), 5sqrt sin (55.3)) Part III: Use the dot product of the vectors and to determine if they are orthogonal. (2 points) U x v = ac+ bd= 0 -6(-42)+13(-34)= 252+ -442= 190 1313-Final-Exam-Semester-Exam-Teacher-Scored-2pdf/Not orthogonal 10. Find the fourth roots of the complex number . Part I: Write z1 in polar form. (2 points) 2(cos60+isin60) Part II: Find the modulus of the roots of z1. (2 points) 2 Part III: Find the four angles that define the fourth roots of the number z1. (4 points) 4th(2)(cos15+isin15) 4th(2)(cos105+isin105) 4th(2)(cos195+isin195) 4th(2)(cos285+isin285) Part IV: What are the fourth roots of ? (4 points) 4root2(cos(7.5)+isin(7.5)) 4root2(cos(97.5)+isin(97.5)) 4root2(cos(187.5)+isin(187.5)) 4root2(cos(277.5)+isin(277.5)) [Show More]

Last updated: 3 years ago

Preview 1 out of 8 pages