Intro to Cryptography WGU C839 Module 3 Questions and Answers 100% Pass

Document Content and Description Below

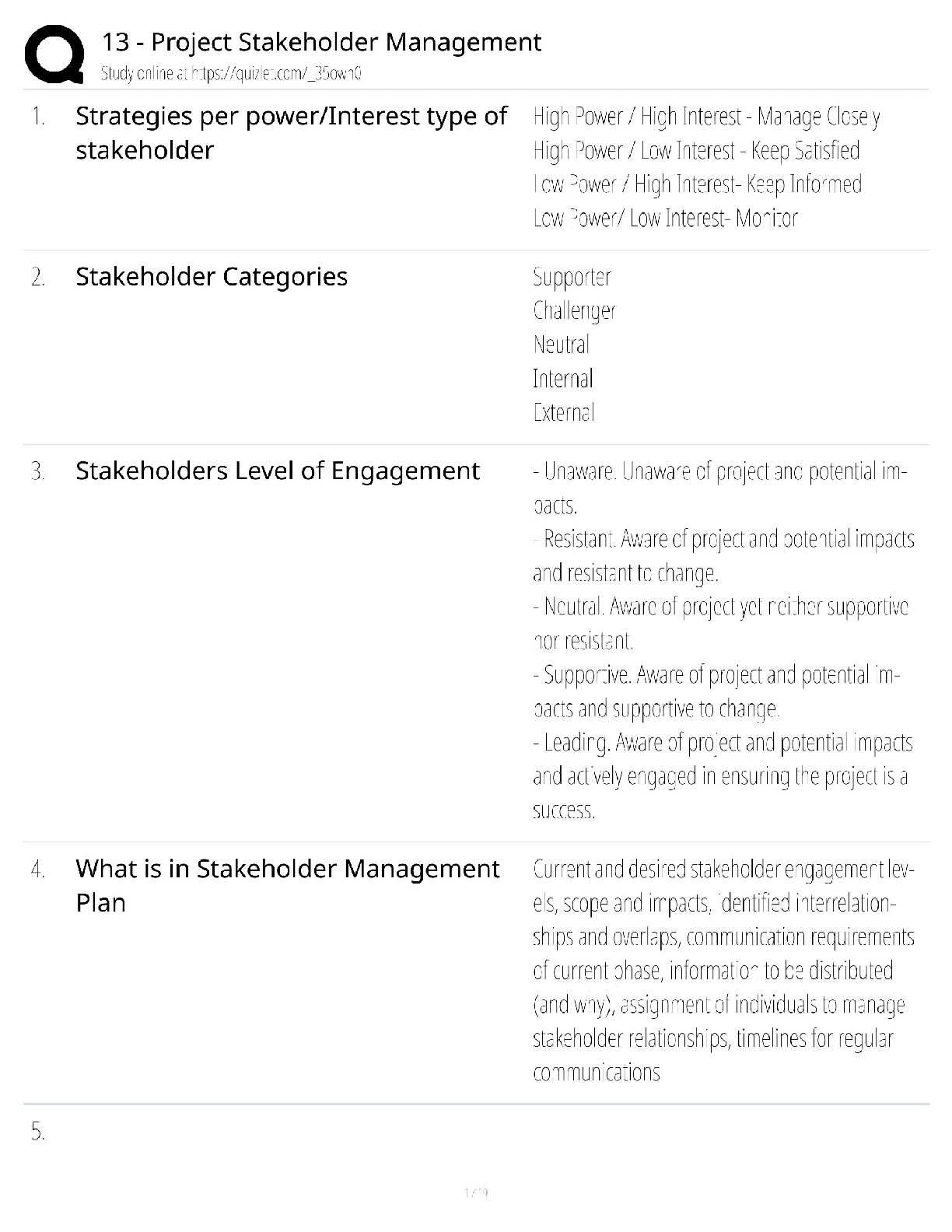
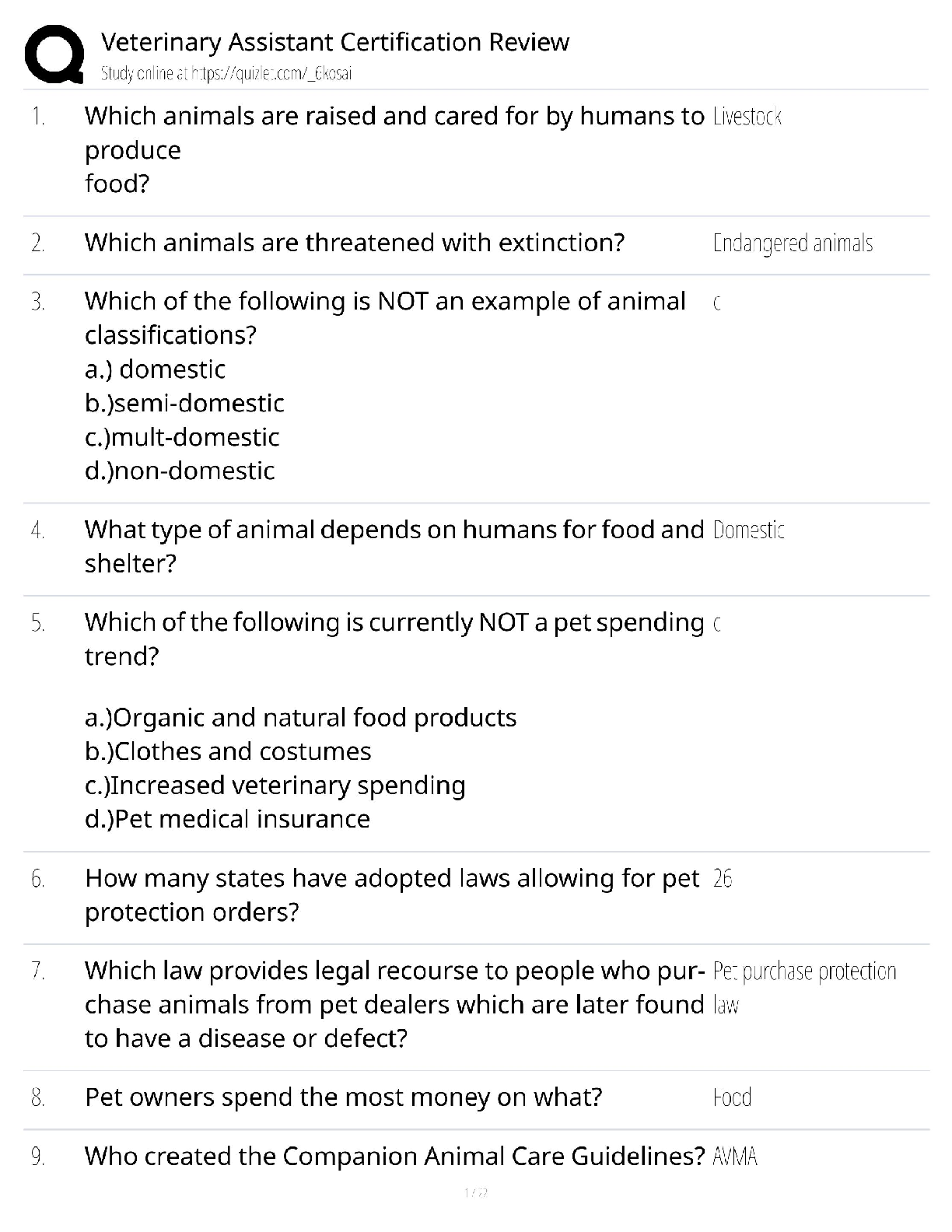
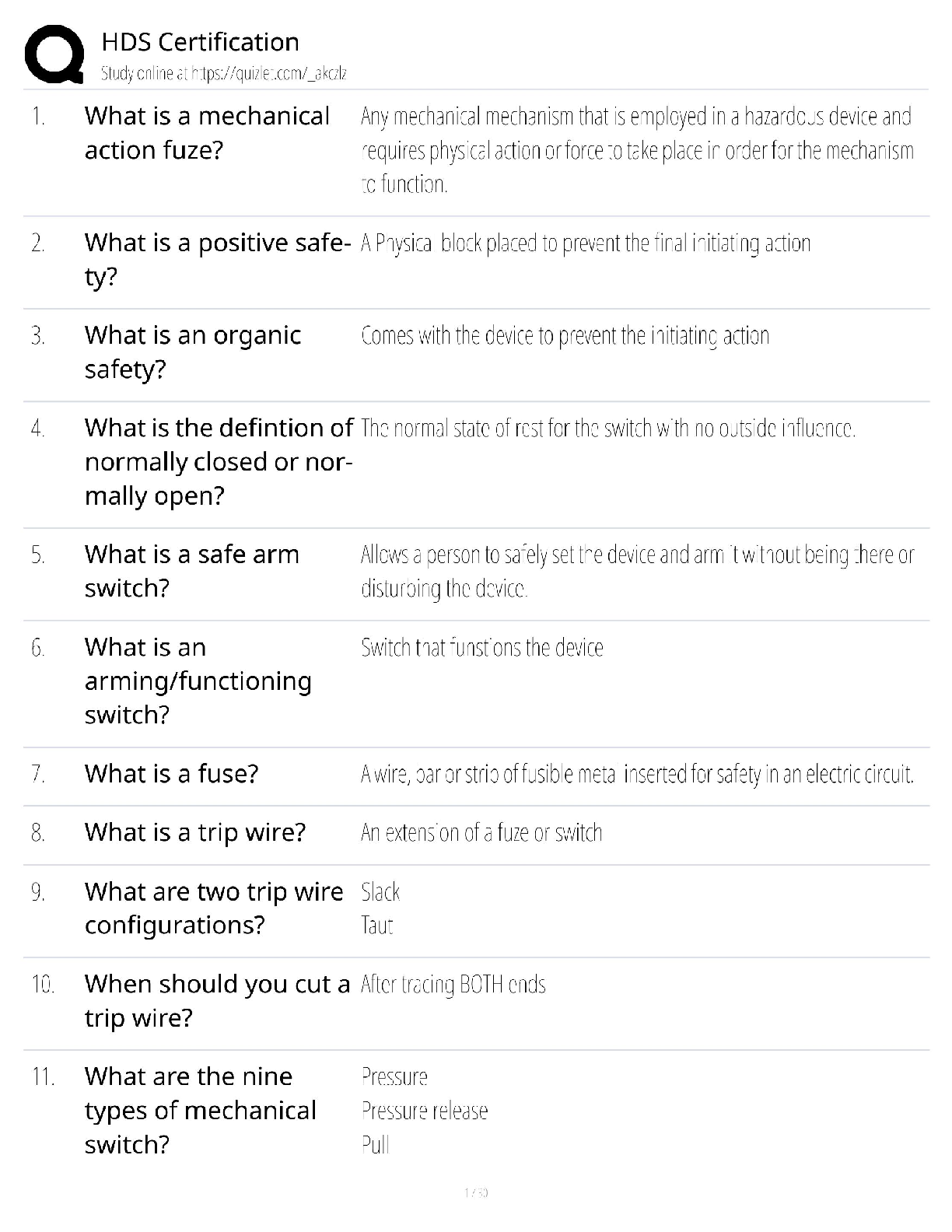
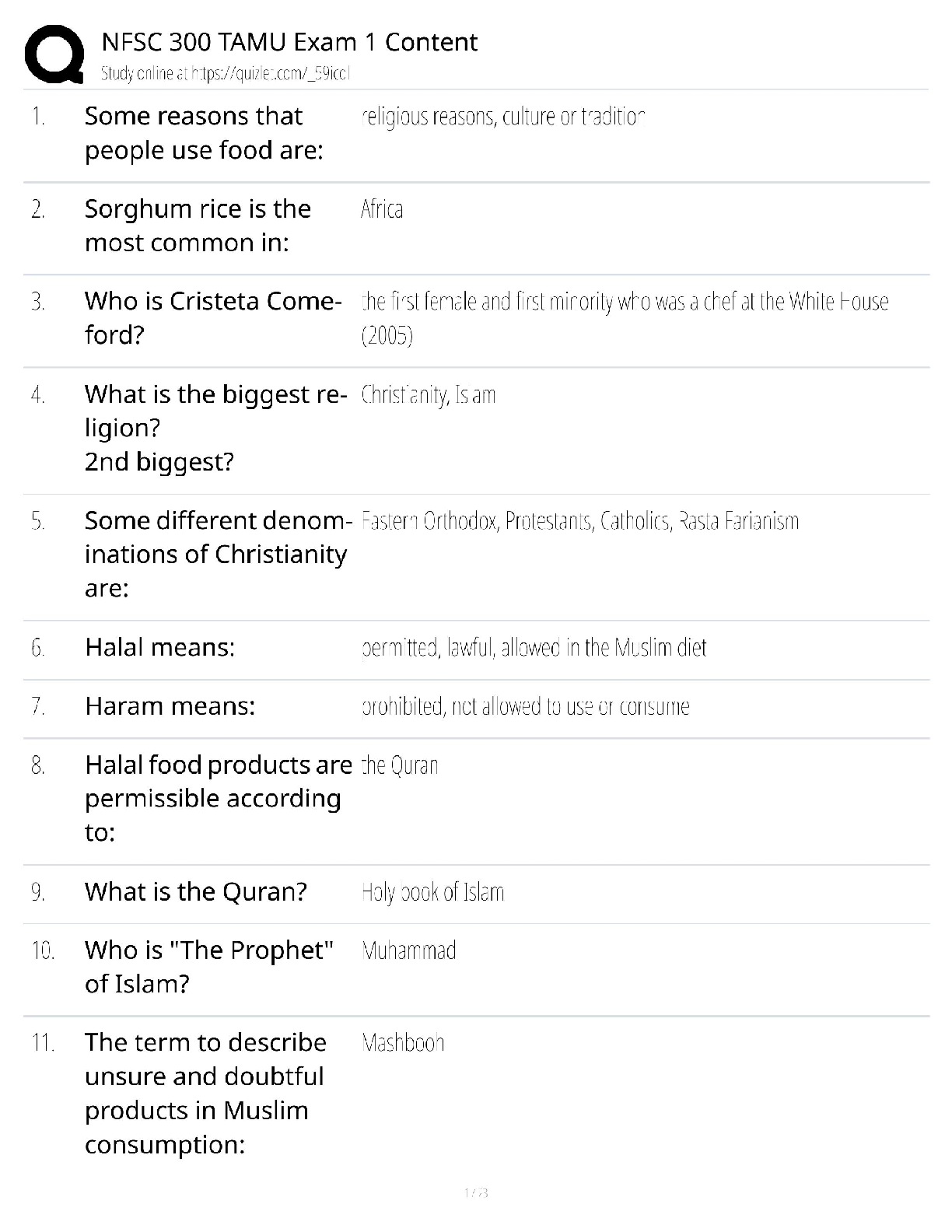
Intro to Cryptography WGU C839 Module 3 Questions and Answers 100% Pass Consists of public and private keys The public key is made public by publishing to a directory or installed on a computer. T... he private key is kept secret Does not involve exchanging a secret key or key exchange The public key is used to encrypt messages only the recipients private key can decrypt ✔✔Asymmetric Cryptography Slower then Symmetric algorithms provides a secure way to communicate provides a method of validation Non-repudiation ✔✔Disadvantages and Advantages of Asymmetric Crypto Denotes the natural numbers. These are also sometimes called the counting numbers. they are 1, 2, 3, etc. ✔✔N Denotes the integers. These are whole numbers -1, 0, 1, 2, etc. The natural numbers combined with zero and and the negative numbers ✔✔Z Denotes the rational number (ratios of integers). Any number that can be expressed as a ratio of two integers. i.e. 3/2, 17/4, 1/5 ✔✔Q Denotes the real numbers. This includes the rational numbers as well as numbers that cannot be expressed as a ratio of two integers, such as √2 ✔✔R Denotes imaginary numbers. These are numbers whose square is a negative √-1 - 1i ✔✔i Having changes to one character in the plaintext affect multiple characters in the ciphertext. ✔✔Diffusion Attempts to make the relationship between the statistical frequencies of the ciphertext and the actual key as complex as possible. Occurs by using a complex substitution algorithm ✔✔Confusion A small change that yields large effects on the output. This is a Fiestel variation on Claude Shannon's concept of diffusion. ✔✔Avalanche In Information Theory this is the measure of the uncertainty associated with a random variable ✔✔Entropy It is impossible to compress the data such that the code rate is less that the Shannon entropy of the source, without it being virtually certain that information will be lost. ✔✔Source Coding Theorem Any number whose factors are 1 and itself ✔✔Prime Numbers If a random number N is selected, the chance of it being a prime is approximately 1 /In(N) where In(N) denotes the natural logarithm of N ✔✔Prime Number Theorem Method for generating prime numbers Mn - 2n -1 Works for n 2, 3, 5, 7 but failed on n = 11 and many other n values ✔✔Mersenne Primes A number that has no factors in common with another number 3 and 7 are one of these. ✔✔Co-Prime Numbers The number of positive integers less than or equal to n that are co-prime to n is called the " " of n. If m and n are co-prime then: Φ(m*n) = φm * φn Φ is the symbol for the Euler phi function ✔✔Euler's Totient Dividing A by N and returning the remainder. i.e. 5 mod 2 = 1 (5/2, 2 * 2 = 4, 5 - 4 = 1) 12 mod 5 = 2 (12/5, 5 * 2 = 10, 12 - 10 = 2) Sometimes symbolized as %, as in 5 % 2 = 1 ✔✔Modulus Operator Sequence of numbers derived by adding the last two numbers to create the next. N1 + N2 = n3 [Show More]

Last updated: 2 years ago

Preview 1 out of 6 pages

Buy Now

Instant download

We Accept: