Questions and Answers>Homework #2 LH 6/17/2020 To begin, this homework requires the following package: install.packages(“tidyverse”, repos = “http://cran.us.r-project.org”)

Document Content and Description Below

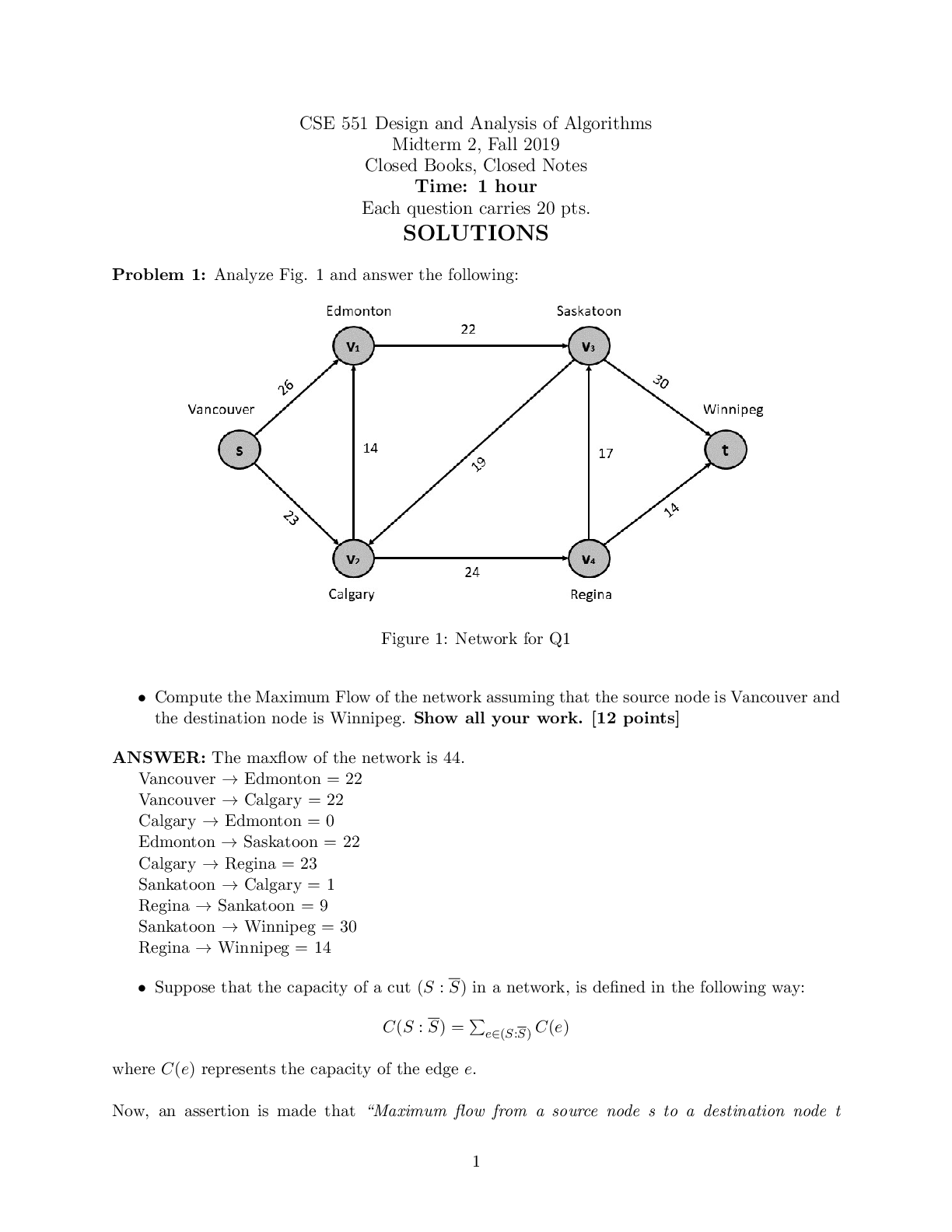
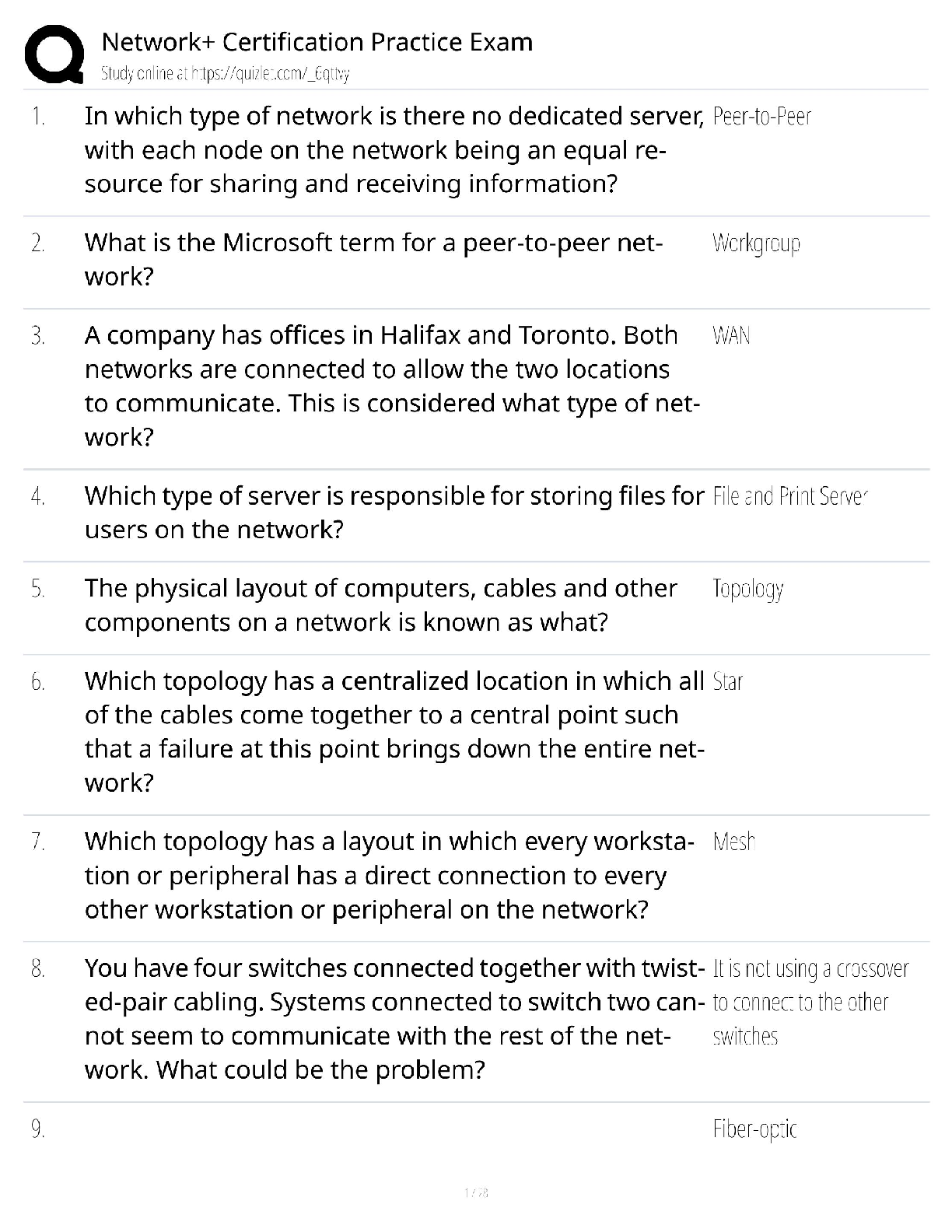
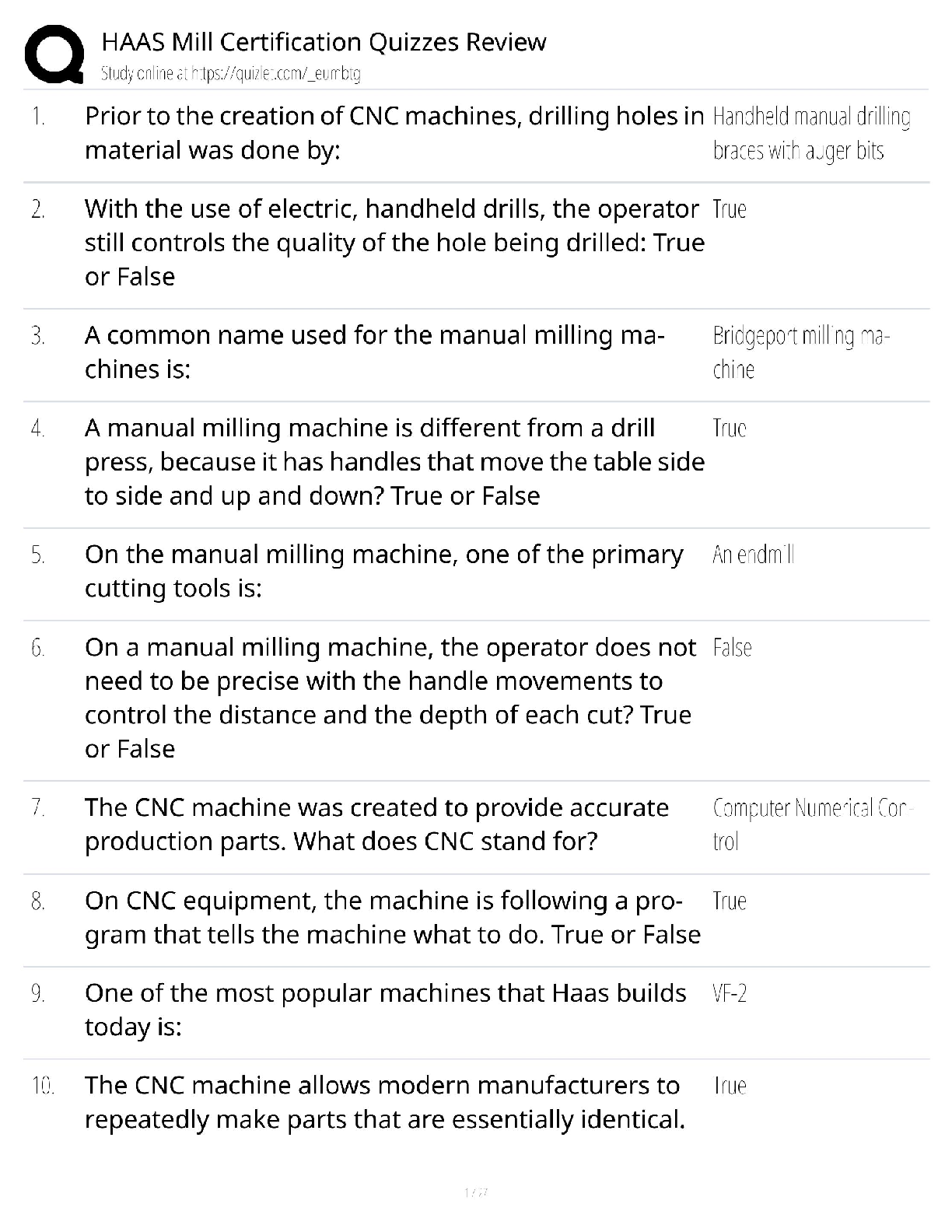
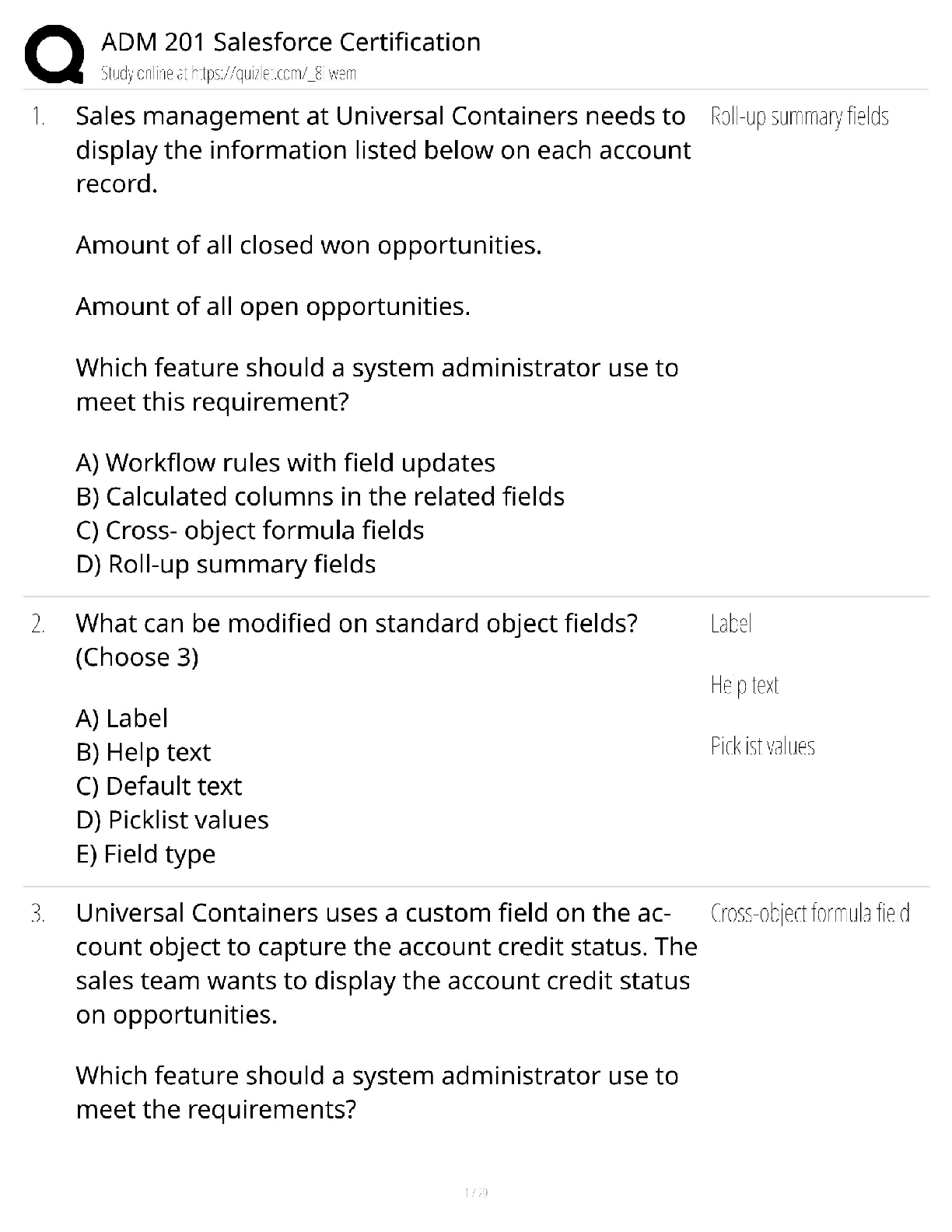
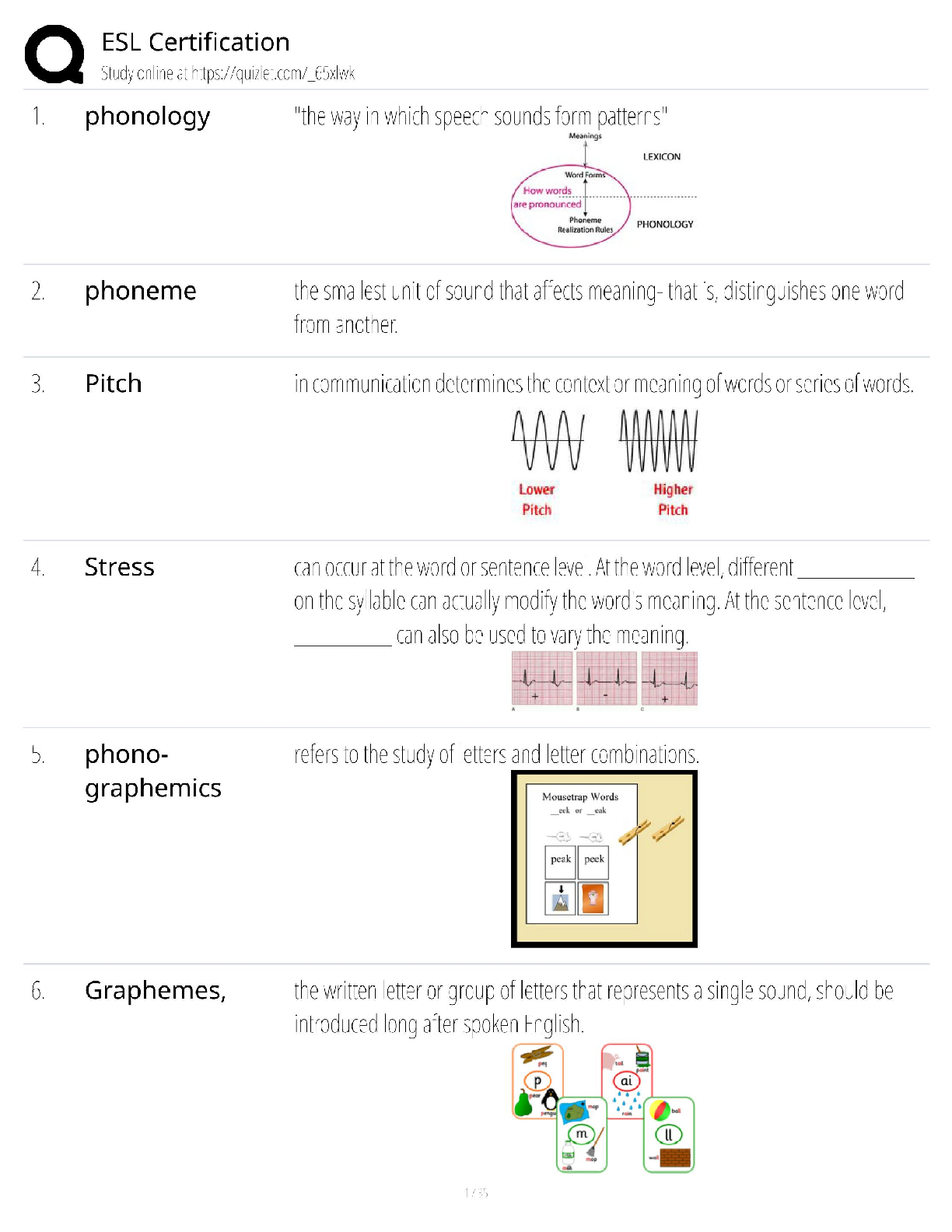
Homework #2 LH 6/17/2020 To begin, this homework requires the following package: install.packages(“tidyverse”, repos = “http://cran.us.r-project.org”) Question 1: For parts A and B: Pla ... ntGrowth is a dataset in R that contains crop weights of a control group and two treatment groups: library(datasets) data(PlantGrowth) attach(PlantGrowth) summary(PlantGrowth) ## ## Min. | weight :3.590 | group ctrl:10 trt1:10 trt2:10 ## 1st Qu.:4.550 ## Median :5.155 ## Mean | :5.073 ## 3rd Qu.:5.530 ## Max. | :6.310(i) Create two separate datasets, one with data points of treatment 1 group along with control group and other with datapoints of treatment 2 group with the control group: trt1 <- filter(PlantGrowth, group=="trt1"|group=="ctrl") trt2 <- filter(PlantGrowth, group=="trt2"|group=="ctrl") 1.A) Now compute the difference estimator for treatment 1 and treatment 2 datasets that were created, in comparison with the control group? First, create a dummy variable indicating “treatment” in each dataset: trt1 <- transform(trt1, treat = ifelse(trt1$group == 'trt1', 1, 0)) trt2 <- transform(trt2, treat = ifelse(trt2$group == 'trt2', 1, 0)) Next, create a linear model for each treatment set using the dummy variable. The coefficient of b1 is the difference estimator for each treatment: 1 #Treatment 1 Model: lm.trt1 <- lm(weight ~ group, data = trt1) summary(lm.trt1)$coefficients ## ## (Intercept) ## grouptrt1 | Estimate Std. Error t value | Pr(>|t|) 5.032 0.2202177 22.85012 9.547128e-15 -0.371 0.3114349 -1.19126 2.490232e-01The difference estimator for treatment 1 is -0.371. #Treatment 2 Model: lm.trt2 <- lm(weight ~ group, data = trt2) summary(lm.trt2)$coefficients ## ## (Intercept) ## grouptrt2 | Estimate Std. Error t value | Pr(>|t|) 5.032 0.1636867 30.74166 5.206846e-17 0.494 0.2314879 2.13402 4.685138e-02The difference estimator for treatment 2 is 0.494. 1.B) From the PlantGrowth dataset what is the average crop weight of the control group, treatment 1 group, and treatment 2 group, comment on which group has the highest average? The mean of the control group is the intercept of either model, which is equal to _5.032__. The mean of the treament 1 group can be calulated by: Diff. Est. + Control Mean = Treatment 1 Mean summary(lm.trt1)$coefficients[2] + summary(lm.trt1)$coefficients[1] ## [1] 4.661 Likewise to find the mean of the treatment 2 group: summary(lm.trt2)$coefficients[2] + summary(lm.trt2)$coefficients[1] ## [1] 5.526 The treatment 2 group had the highest average weight (5.526), which means that the plants grew the most due to the experimental “treatment” than both the control group and the treatment 1 group. This treatment could be the type or amount of fertilizer applied applied to the treatment 2 group, for example. (Note that treatment 1 group had a lower average (4.661) than the control group, which means that the treatment applied actually resulted in less growth than the control group.) For parts C, D, and E: using the dataset Min_Wage.csv minwage <- read_csv("Min_Wage.csv") ## Parsed with column specification: ## cols( ## ## ## ## ## ## | d = col_double(), d_nj = col_double(), fte = col_double(), bk = col_double(), kfc = col_double(), roys = col_double(),2 ## wendys = col_double(), ## co_owned = col_double(), ## centralj = col_double(), ## southj = col_double(), ## pa1 = col_double(), ## pa2 = col_double(), ## demp = col_double(), ## State = col_character() ## ) attach(minwage) 1.C) Classify the workers into four groups and assign the corresponding group with the group title (A, B, C, and D) (i.e., control group before change to the group A etc.). where the group titles are as follows in the table below: Type | Before After Control: A Treated: B | C DClassify the groups, as assigned: #A = Philadelphia before NJ tax change #B = NJ before tax change #C = Philadelphia before NJ tax change #D = NJ after tax change #assign above groups: minwage$class <- ifelse(State=='Philadelphia' & d==0, 'A', ifelse(State=='Philadelphia' & d==1, 'C', ifelse(State=='New Jersey' & d==0, 'B', ifelse(State=='New Jersey' & d==1, 'D', '')))) minwage$class <- as.factor(minwage$class) #display number of records / data points in each group #there are 75 Philadelpha points (ea. before and after, A & C) #and 309 NJ points (ea. before and after, B & D) summary(minwage$class) ## A B C D ## 75 309 75 309  [Show More]

Last updated: 2 years ago

Preview 1 out of 8 pages