Electrical Engineering > QUESTIONS & ANSWERS > CS 4141 - University of Texas, Dallas_CS 4141 Pre-Lab 3. Adder IC (74LS283), Subtraction with Two’ (All)

CS 4141 - University of Texas, Dallas_CS 4141 Pre-Lab 3. Adder IC (74LS283), Subtraction with Two’s Complement, 1-digit BCD Full Adder. Q&A

Document Content and Description Below

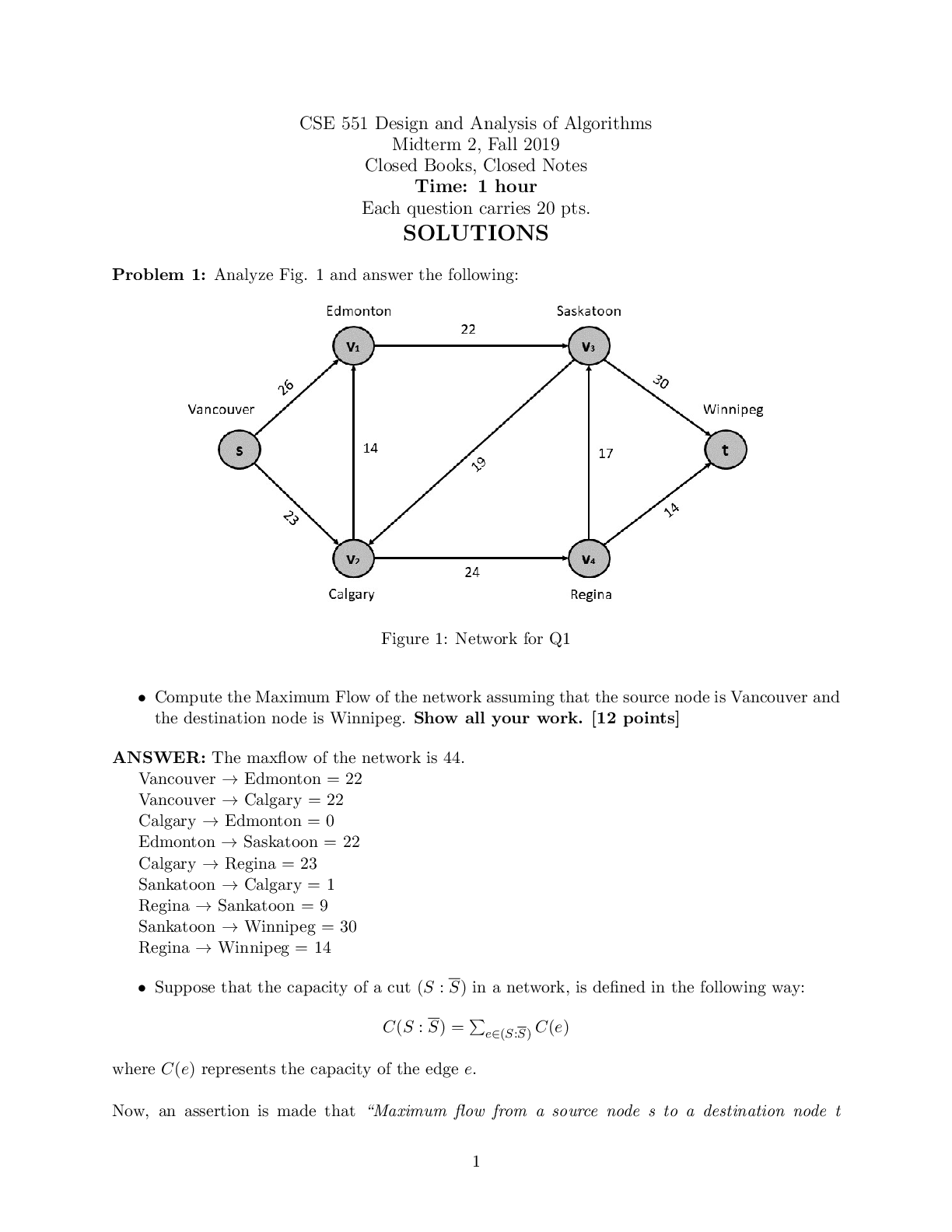
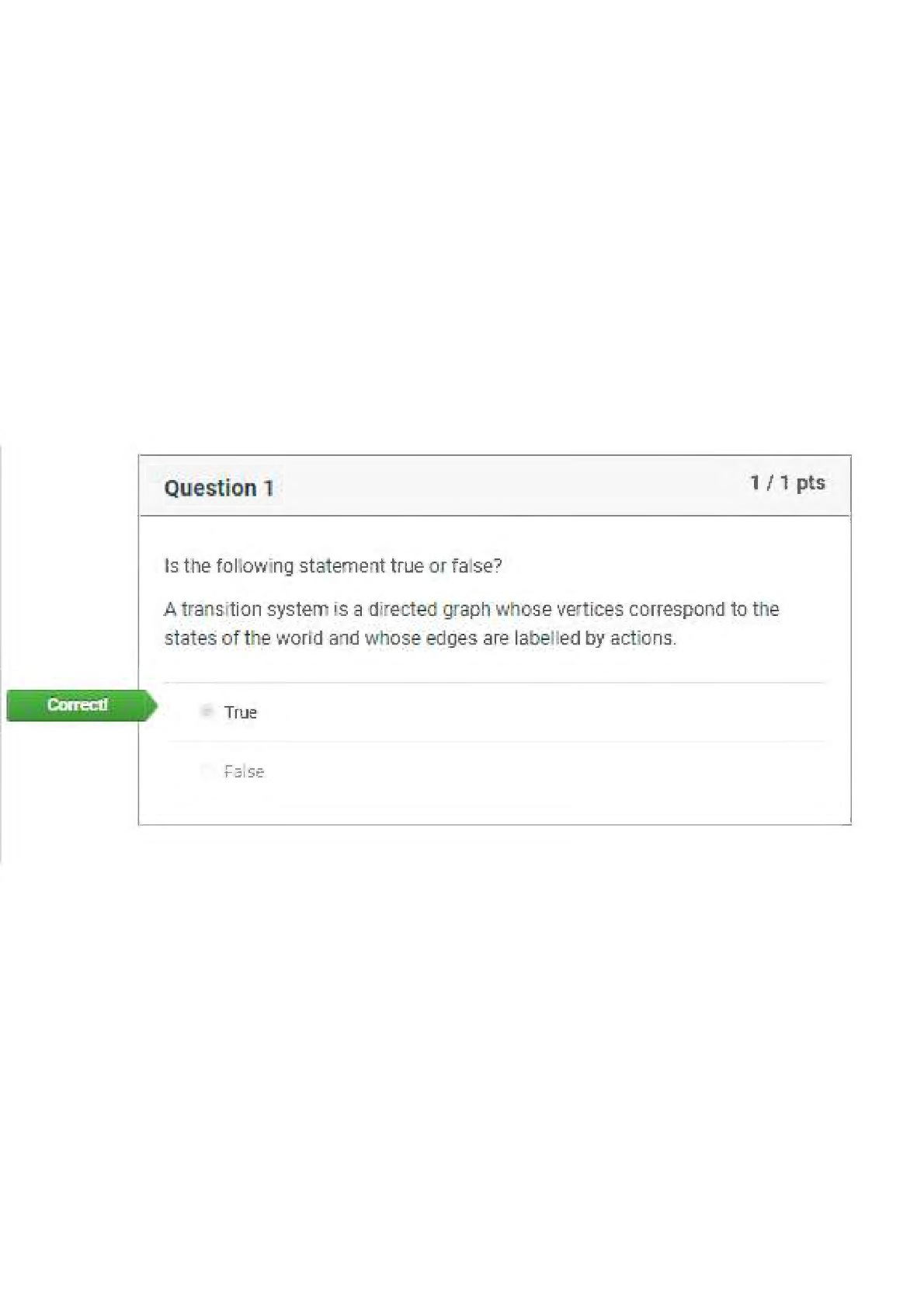
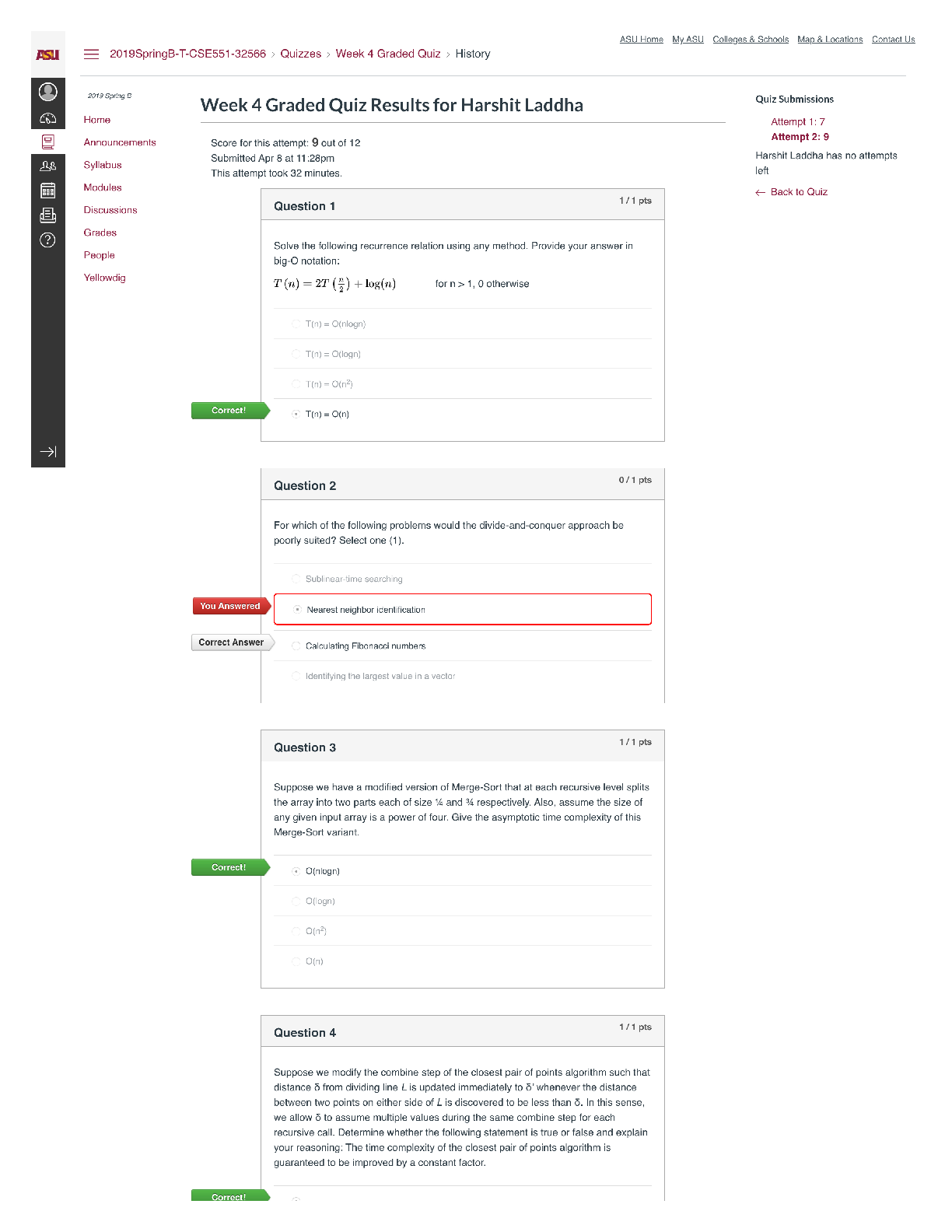
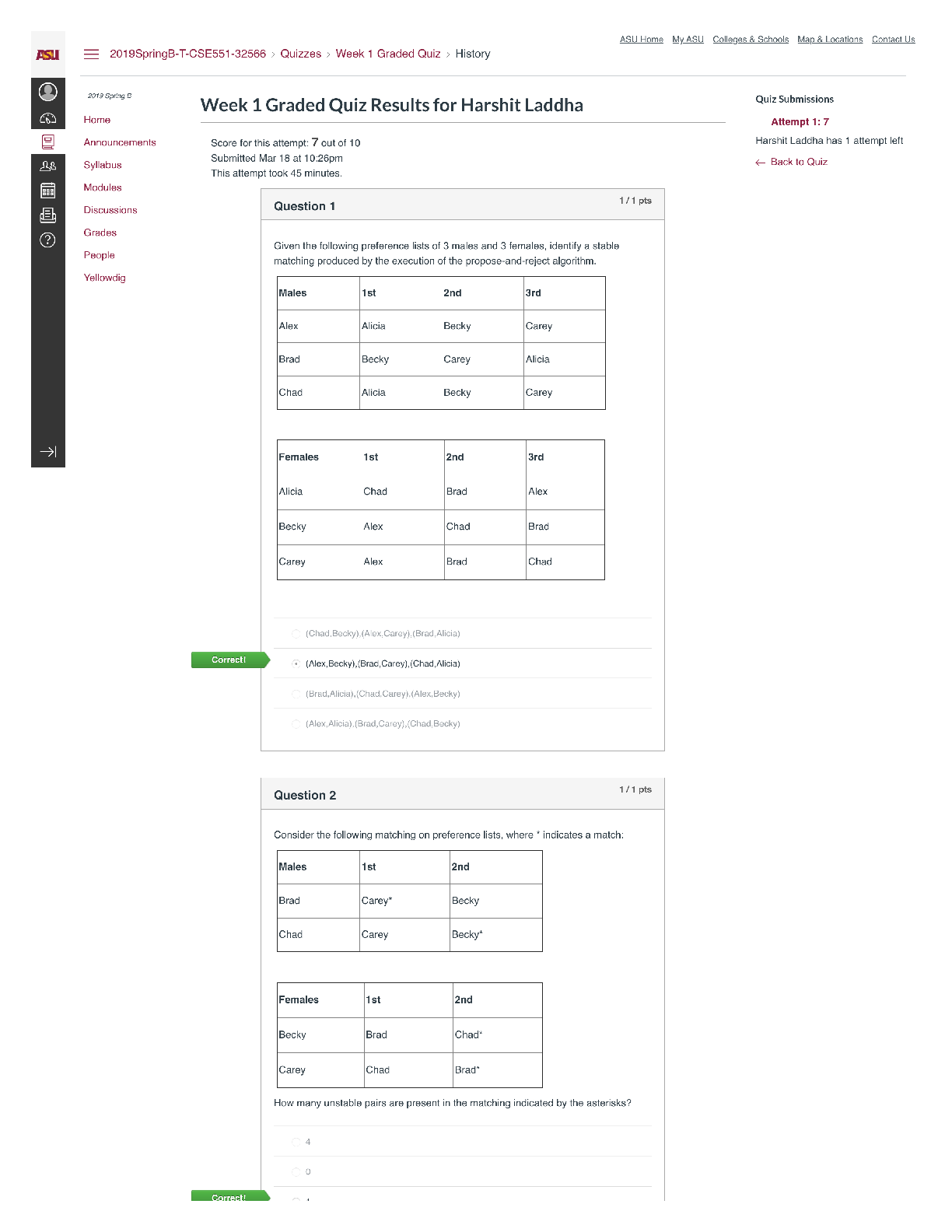
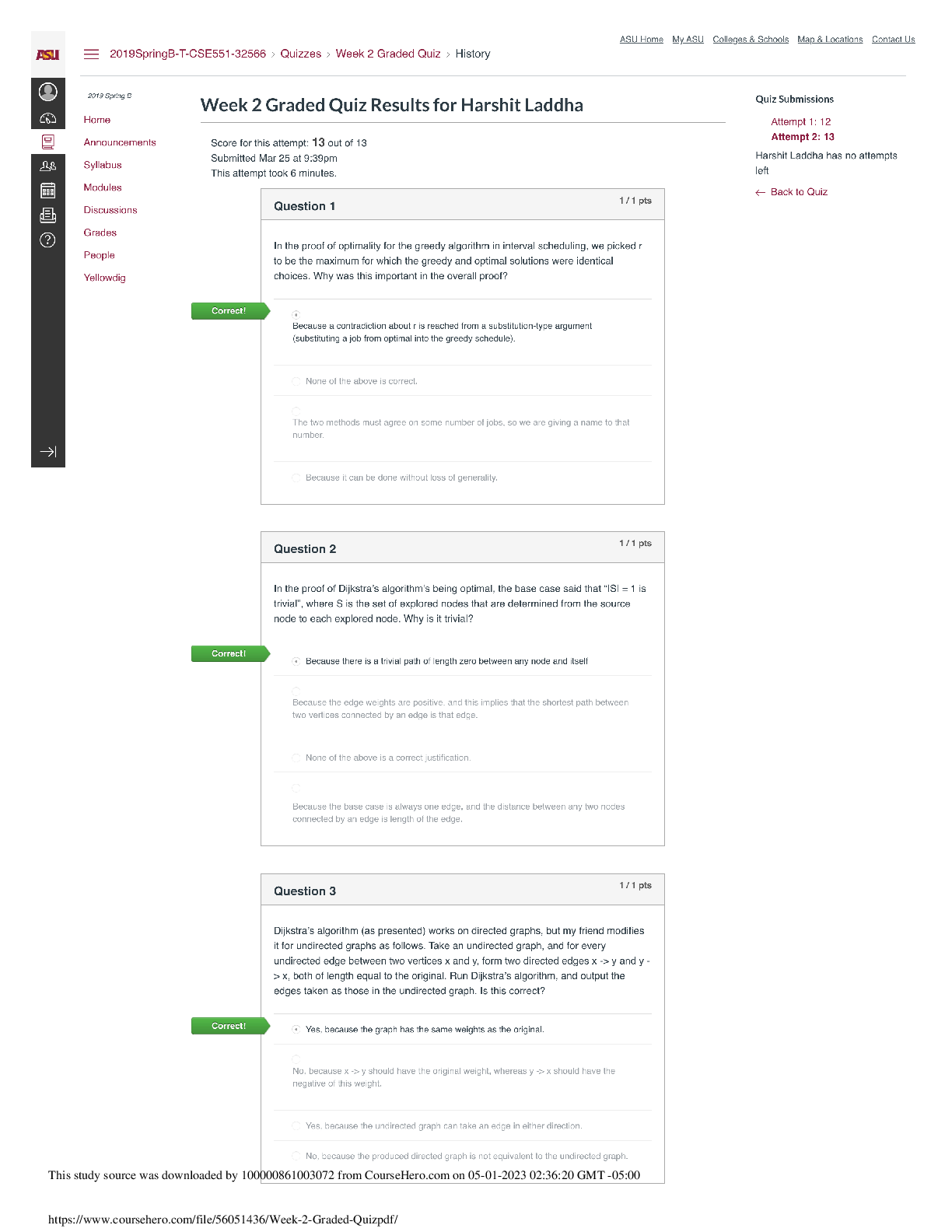
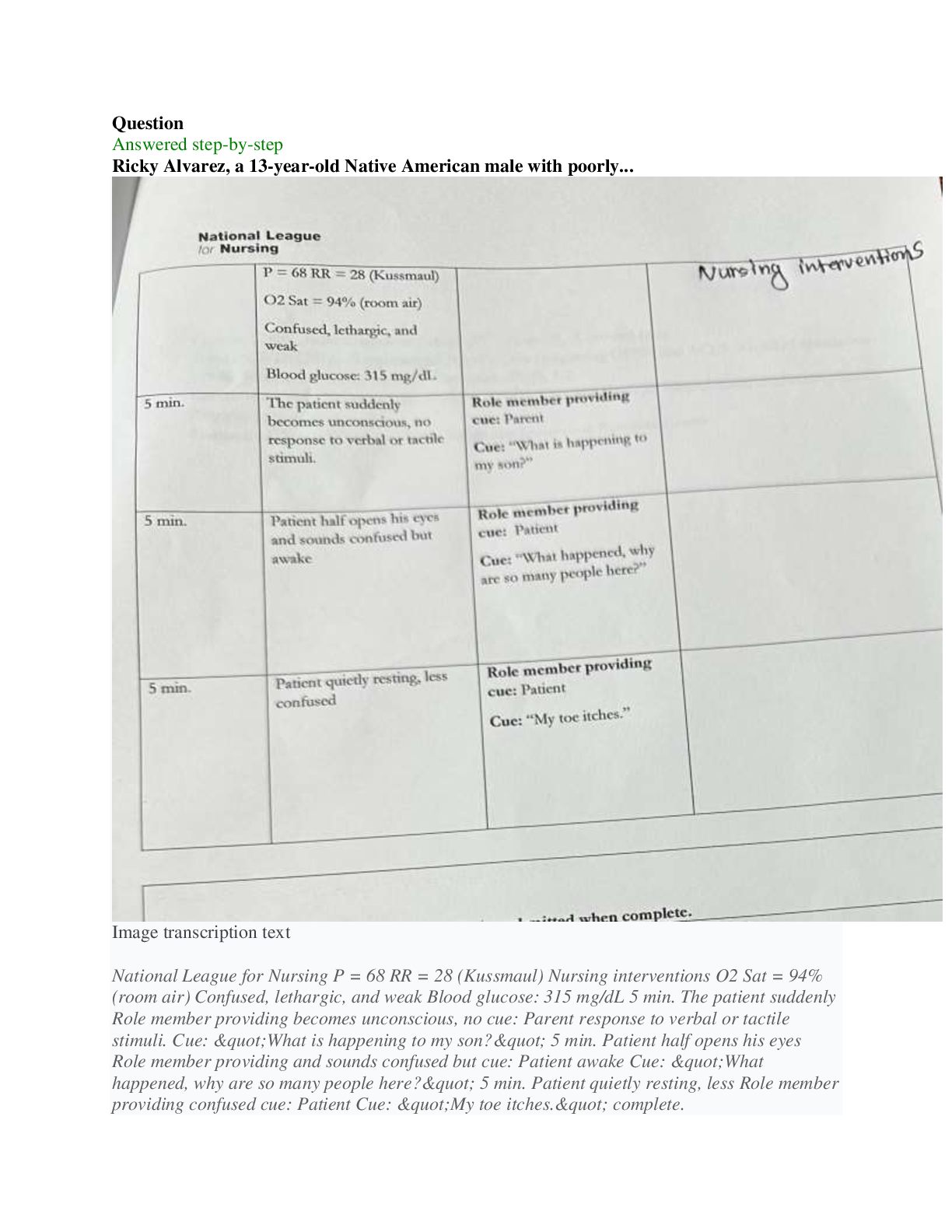
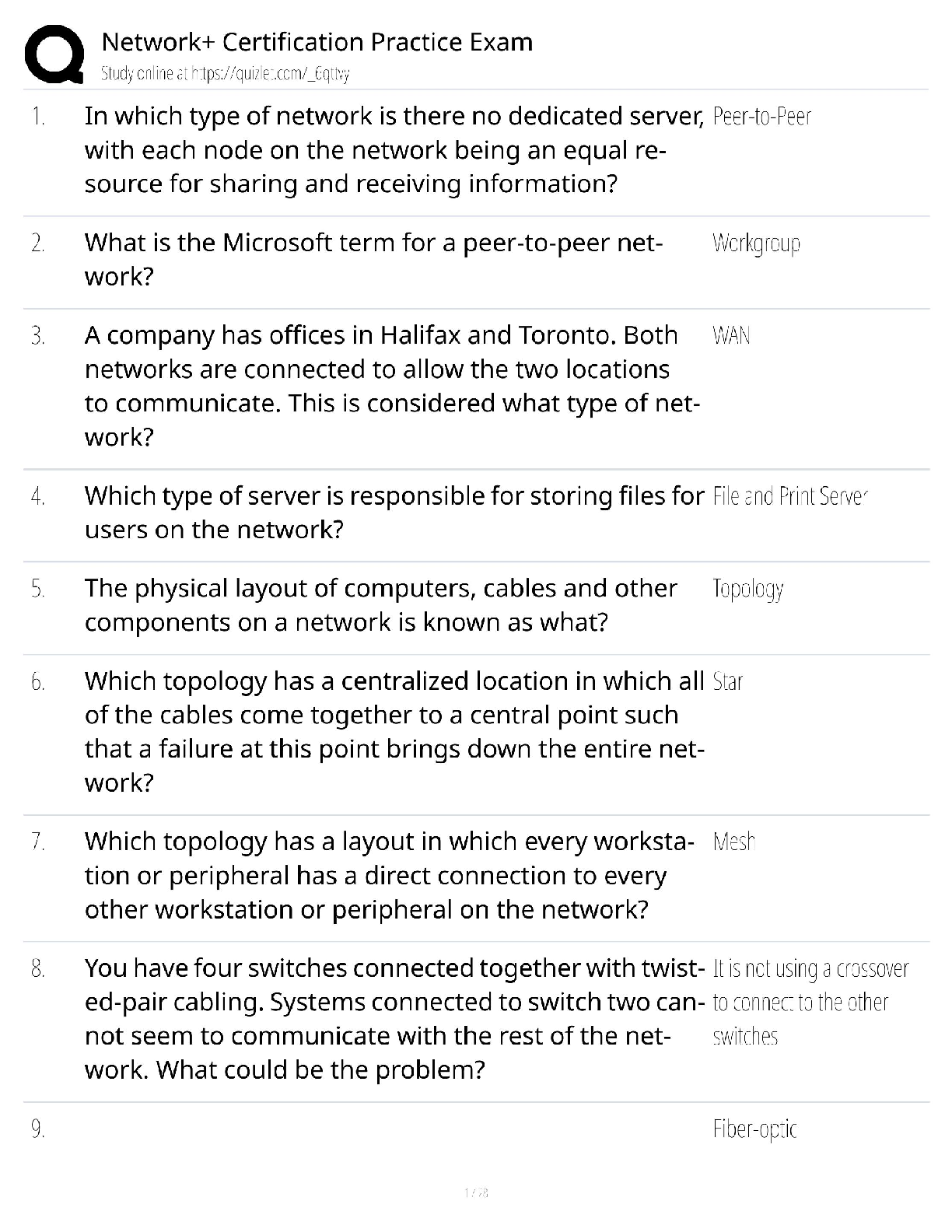
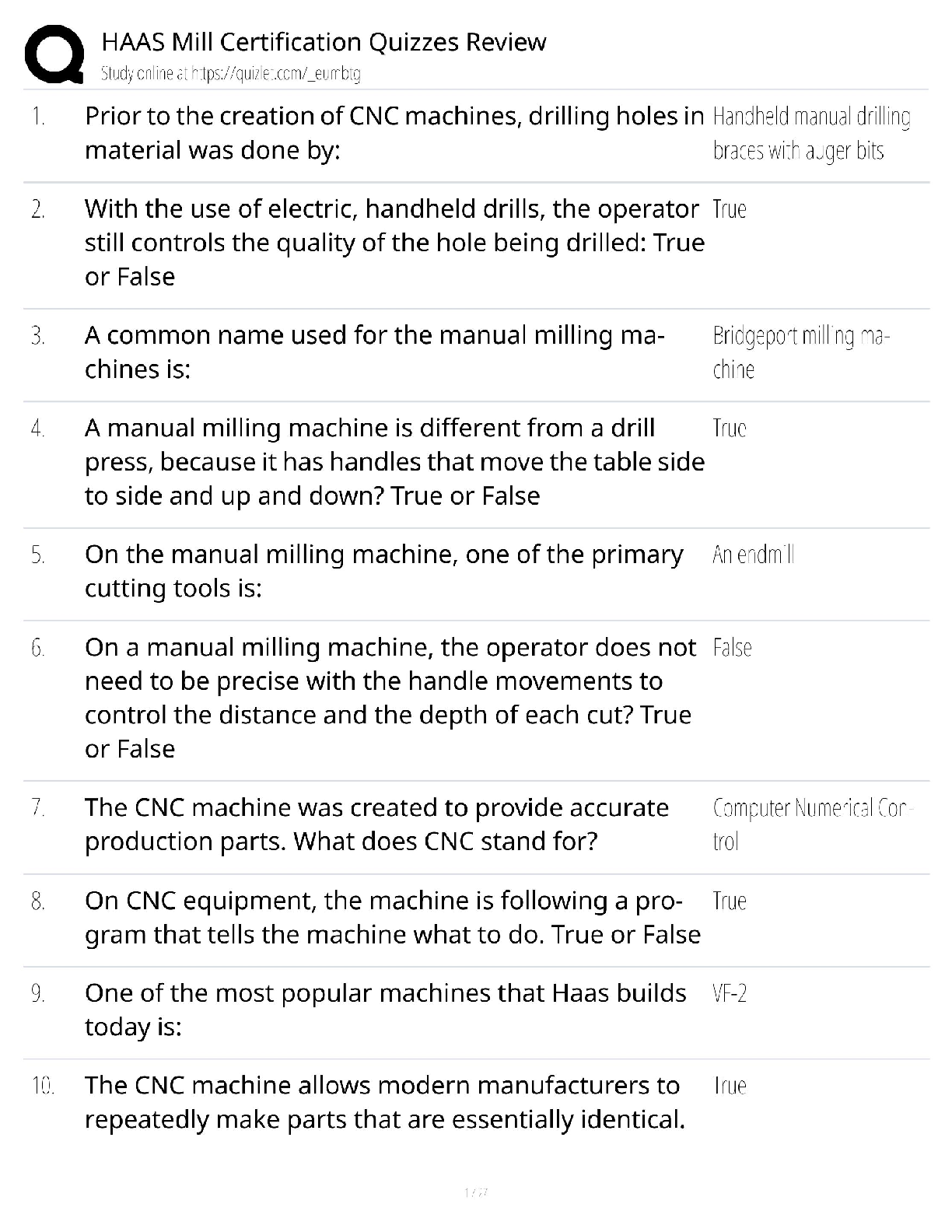
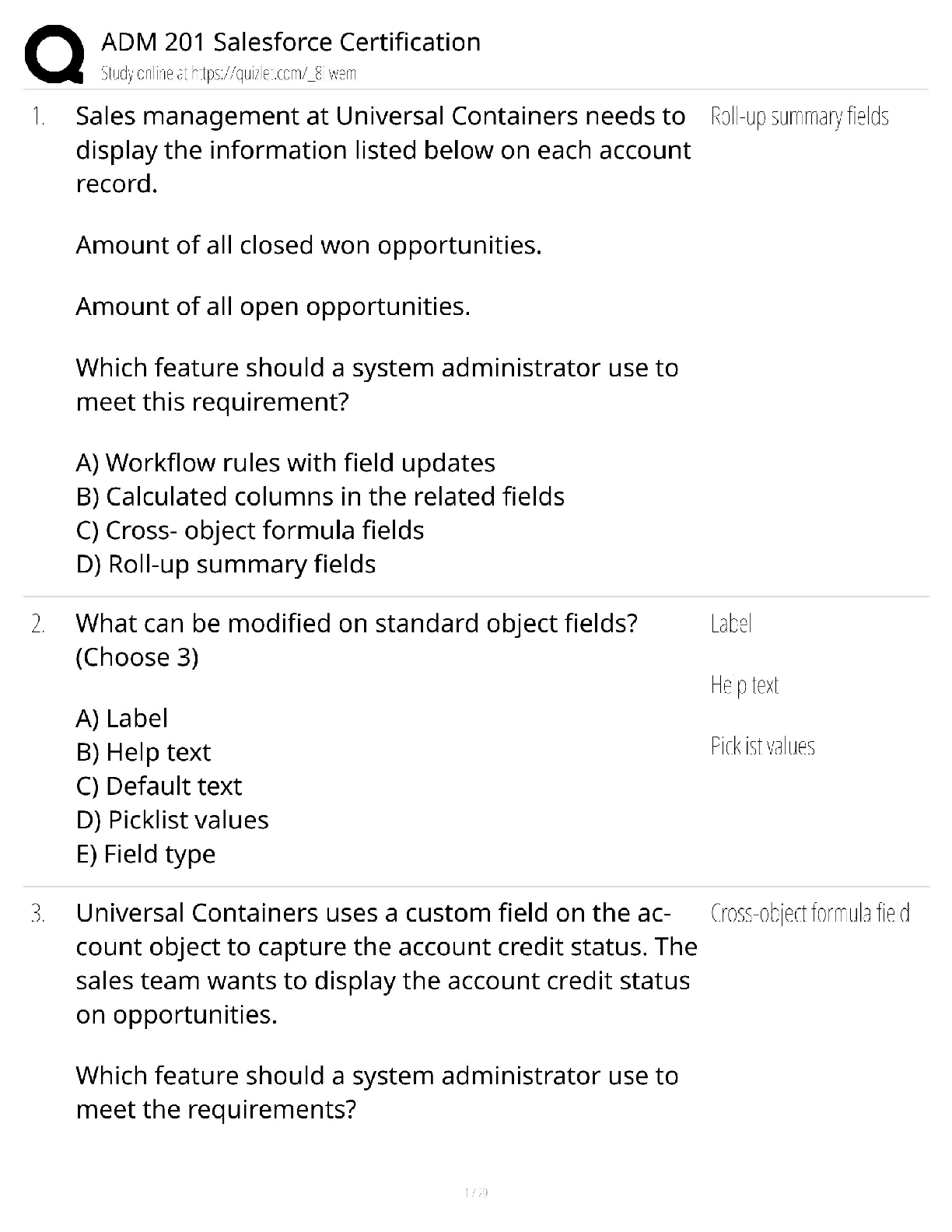
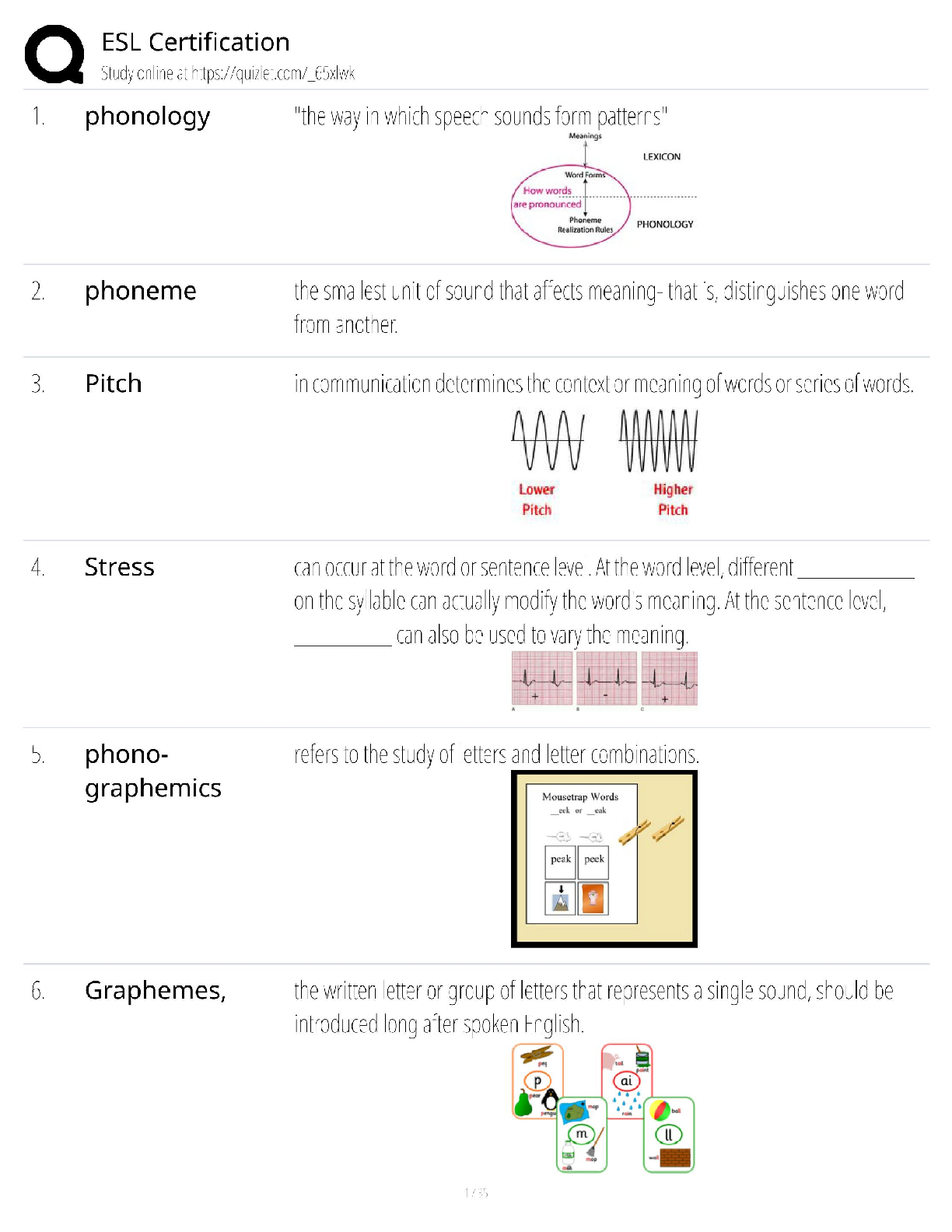
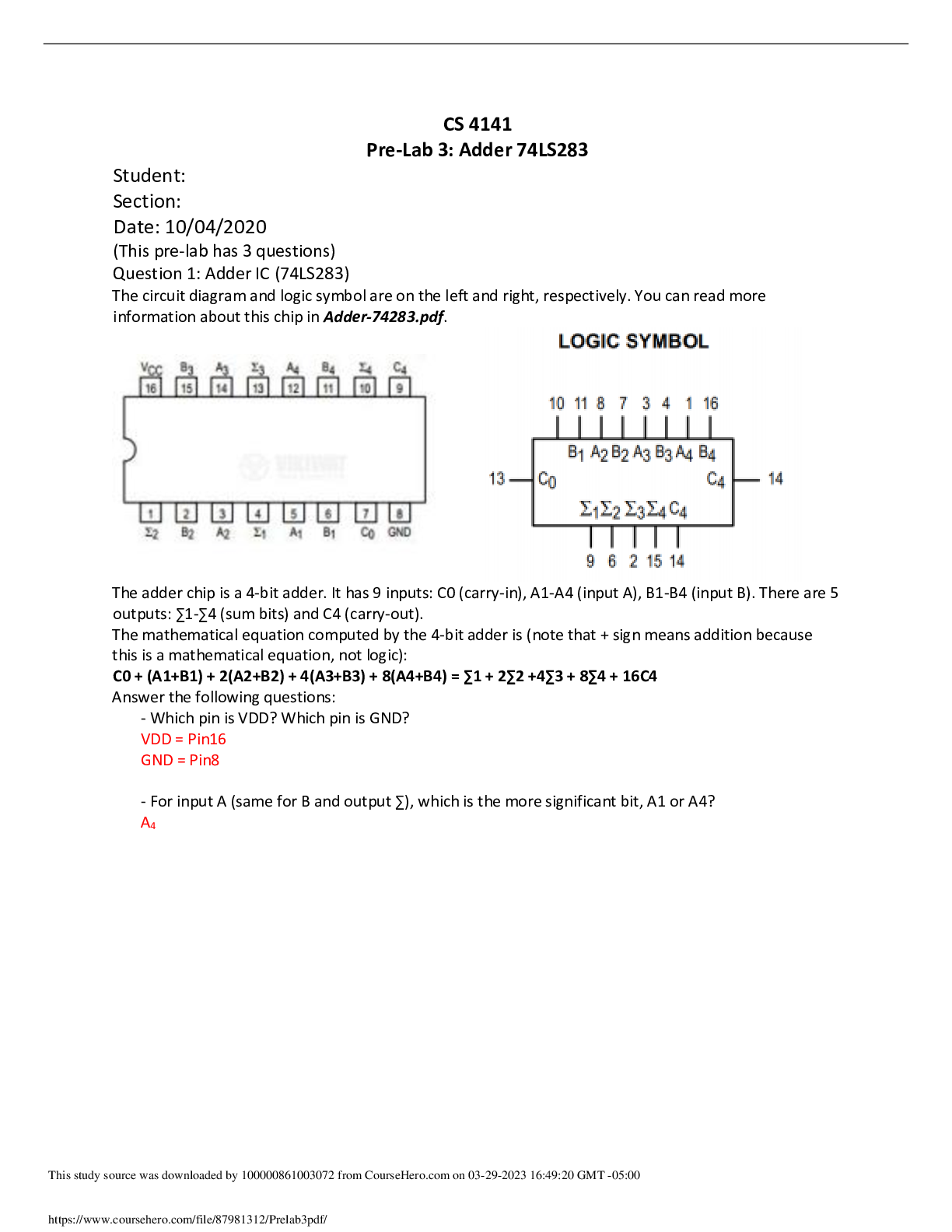
CS 4141 - University of Texas, Dallas_CS 4141 Pre-Lab 3. Adder IC (74LS283), Subtraction with Two’s Complement, 1-digit BCD Full Adder. Q&A CS 4141 Pre-Lab 3: Adder 74LS283 Student: Section: Dat ... e: 10/04/2020 (This pre-lab has 3 questions) Question 1: Adder IC (74LS283) The circuit diagram and logic symbol are on the left and right, respectively. You can read more information about this chip in Adder-74283.pdf. The adder chip is a 4-bit adder. It has 9 inputs: C0 (carry-in), A1-A4 (input A), B1-B4 (input B). There are 5 outputs: ∑1-∑4 (sum bits) and C4 (carry-out). The mathematical equation computed by the 4-bit adder is (note that + sign means addition because this is a mathematical equation, not logic): C0 + (A1+B1) + 2(A2+B2) + 4(A3+B3) + 8(A4+B4) = ∑1 + 2∑2 +4∑3 + 8∑4 + 16C4 Answer the following questions: - Which pin is VDD? Which pin is GND? - For input A (same for B and output ∑), which is the more significant bit, A1 or A4? - Write two examples of using the adder. Compute 10 + 11 and 4 + 6. Note that the numbers are in decimal and + means sum. The sum of 10 + 11 = 21, and 4 + 6 = 10. Show the values for each input bit and output bit of the adder in these computations. Tip: if your input does not require all 4 bits, then the more significant bit(s) must be connected to 0 (GND). You can ignore the more significant bit outputs, but not the inputs. Question 2: Subtraction with Two’s Complement Note: the inputs should be two 2-bit positive numbers (greater than 0). You should only use 2 bits to represent both 2-bit inputs. This will cause problem for representing negative number such as -3. If we can use 3 bits, then -3 will be 101 in two’s complement. But we can use only 2 bits for inputs, then we need to use 01 as -3. In other words, the magnitude of the result will be correct, but the most significant bit will not be correct. For question 2 in the lab, you need to construct a 2-bit adder/subtractor using the 4-bit chip. The adder part is easy, you just need to connect the more significant bits of the inputs to 0 appropriately. For the subtraction, the idea is using 2’s complement. To compute A – B, we compute A + ~(B) + 1, where ~(B) means inverting each bit of input B. To compute A + B, we compute A + B as normal. Let C0 be the toggle between doing add and subtract; i.e. when C0 = 1, we do subtract, and when C0 = 0, we do add. Then we can have the following logic: If C0 = 1, we compute A + ~(B) + C0 = A + ~(B) + 1 If C0 = 0, we compute A + B + C0 = A + B + 0 The remaining problem is inverting bits of B when C0 = 1, and keeping bits of B as usual when C0 = 0. Solve this problem and you will have a 2-bit adder/subtractor. For this question, do the following: - Explain how you manipulate the bits of B to do both add and subtract. [Show More]

Last updated: 2 years ago

Preview 1 out of 5 pages

Buy Now

Instant download

We Accept: