Electrical Engineering > QUESTIONS & ANSWERS > York University Department of Electrical Engineering and Computer Science. EECS 1028 M. FINAL EXAM, (All)

York University Department of Electrical Engineering and Computer Science. EECS 1028 M. FINAL EXAM, 2020 + SOLUTIONS

Document Content and Description Below

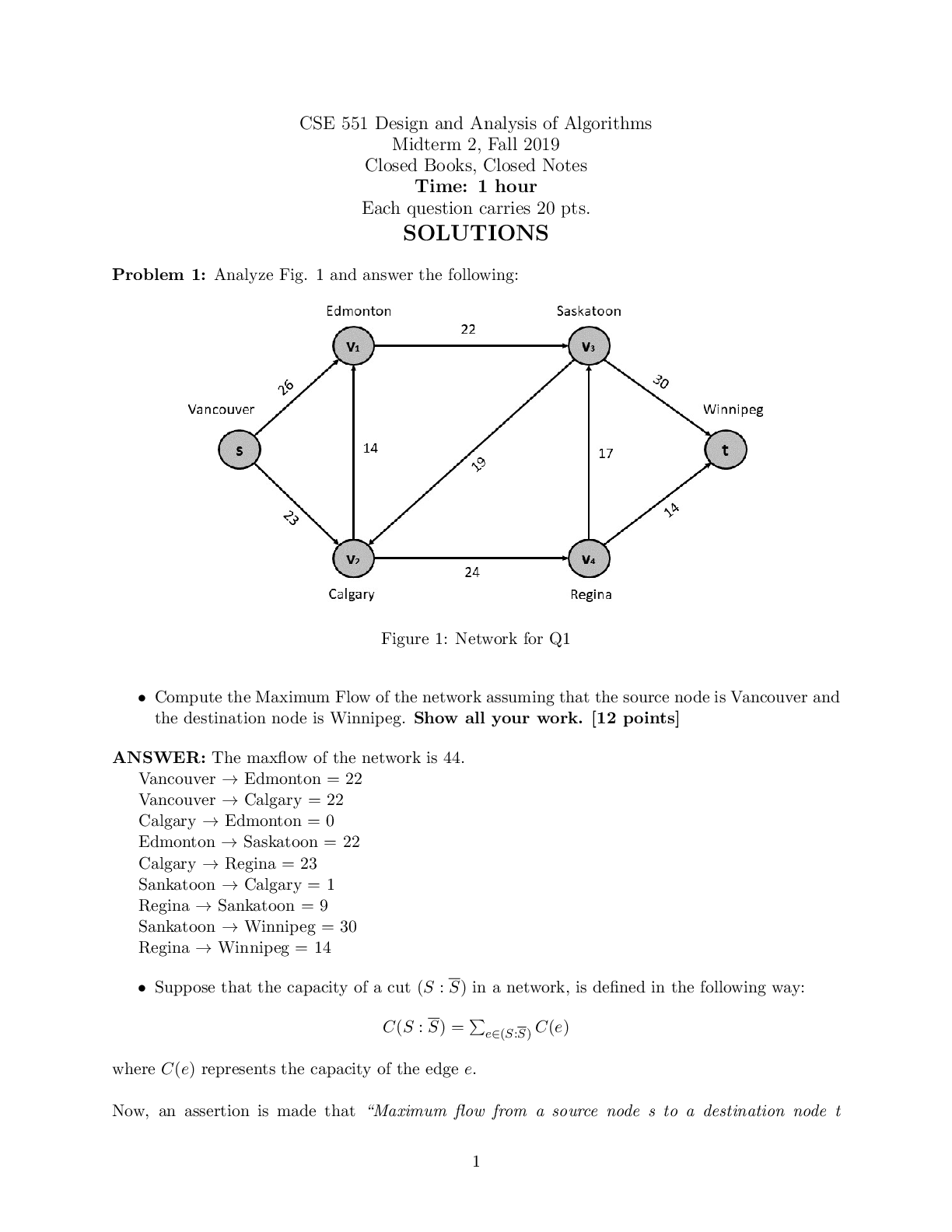
York University Department of Electrical Engineering and Computer Science Lassonde School of Engineering EECS 1028 M. FINAL EXAM, April 9, 2020 SOLUTIONS Professor George Tourlakis Question 1. � ... � Intended version and its solution. (a) (1 MARK) Does Principle 3 refer to \stages"? (Yes/No) Answer. NO! (b) (3 MARKS) Using said principle prove that if R is an equivalence relation on a set A then A=R that denotes the set of all the equivalence classes of R is also a set. Proof. (From our lecture notes!) We know that A=R Def = f[x]R : x 2 Ag Note (a) Each equivalence class [x]R is associated with at least one member x from A that we may think of as an index for [x]R. Any y 2 [x]R serves as index for the same equivalence class as well, since for such y, we have [x]R = [y]R. (b) It is not possible for two distinct equivalence classes [x]R and [y]R to share some index z from A. By the nature of indexing |i.e., that x is an index of [x]R| this would require z 2 [x]R and z 2 [y]R, which implies (class and lecture notes!) that [x]R = [z]R = [y]R, a contradiction to the distinctness of [x]R and [y]R. (c) Thus, Principle 3 applies |recall that Principle 3 requires that there is NO index sharing between two distinct indexed objects. Therefore, since A is a set and its members serve as indices for the members of the set A=R, where no two distinct members of the latter share an index, we have by Principle 3, that A=R is a set. • Unintended version, but is as stated in the paper: Using here Principle 2, as stated in paper. (a) Answer. YES! Part two (Forcing the explicit mention of Principle 2). A is a set. Say it is built at stage Σ (this invokes Prin. 1). But each [x] in A=R is a subset of A so it is built in some stage Σ0 x ≤ Σ. By Principle 2 there IS a stage Σ2 after Σ. At stage Σ2 all [x] are already built and I can collect them to form A=R as a SET (by Prin. 0). Part two shortcut (without explicit mention of Principle 2). If A is a set, then so is 2A (this uses Prin. 2 exactly as immediately above; see notes!). But A=R ⊆ 2A, so A=R is a set!EECS 1028 M Mid Term Test March 2020 Question 2. Consider the congruence modulo 5, \≡5". We know that it is an equivalence relation on Z. (a) (1 MARK ) How many equivalence classes does ≡5 have? [Show More]

Last updated: 2 years ago

Preview 1 out of 5 pages

Buy Now

Instant download

We Accept: