Computer Science > QUESTIONS & ANSWERS > COMPSCI 3SD3 - COMP SCI 3SD3 Virtual Take Home Examination (All)

COMPSCI 3SD3 - COMP SCI 3SD3 Virtual Take Home Examination

Document Content and Description Below

COMP SCI 3SD3 Virtual Take Home Examination McMaster University Final Examination Total: 132 pts ● THIS EXAMINATION PAPER HAS 5 PAGES AND 9 QUESTIONS. ● The exam starts at 12:30 pm and ends at ... 3:30 pm, i.e. 180 (3hr) minutes (for students without extra time permissions). This includes the exam time (150 minutes) plus extra time for technology (30 minutes). ● Please submit the solutions via Avenue using the same procedure as for the assignments. ● Also, just in case, send the solutions via e-mail to janicki@mcmaster.ca . 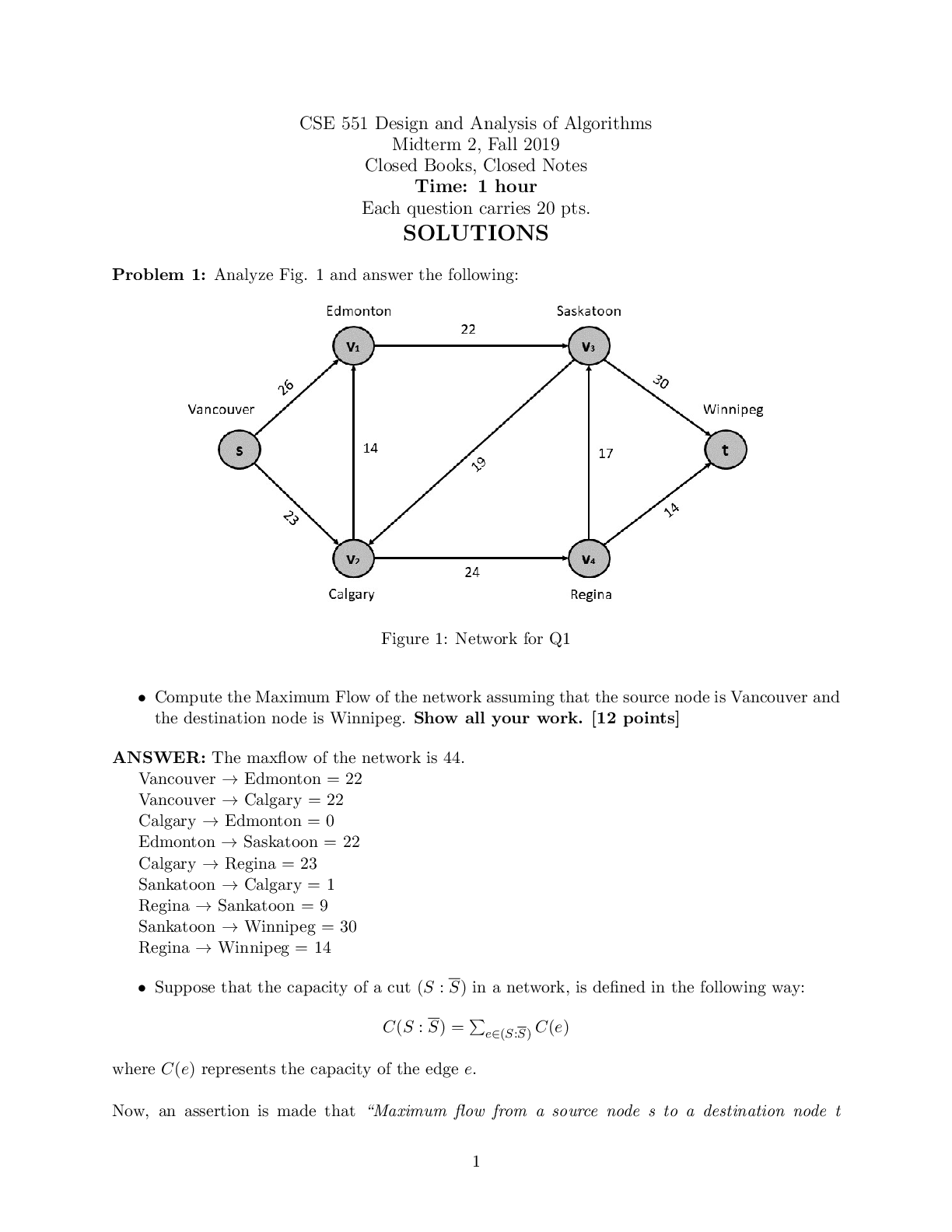● Any question during this midterm, ask by sending an e-mail to Ryszard Janicki (janicki@mcmaster.ca) 1.[10] Consider the following scenario: An office is used by several workers sharing a single printer. As a simplification of a real life scenario, it is assumed that the printer is able to print any number of jobs, independently of the number of pages those jobs have, before running out of toner. The toner is replaced by a technician whenever necessary. a.[5] Provide an FSP description of the above scenario. You must provide also a brief description of the intended behavior for each one of the processes you define. Hint: Possible processes for the above scenario are PRINTER, USER and TECHNICIAN. b.[5] Provide a Petri nets (any kind) description of the above scenario. 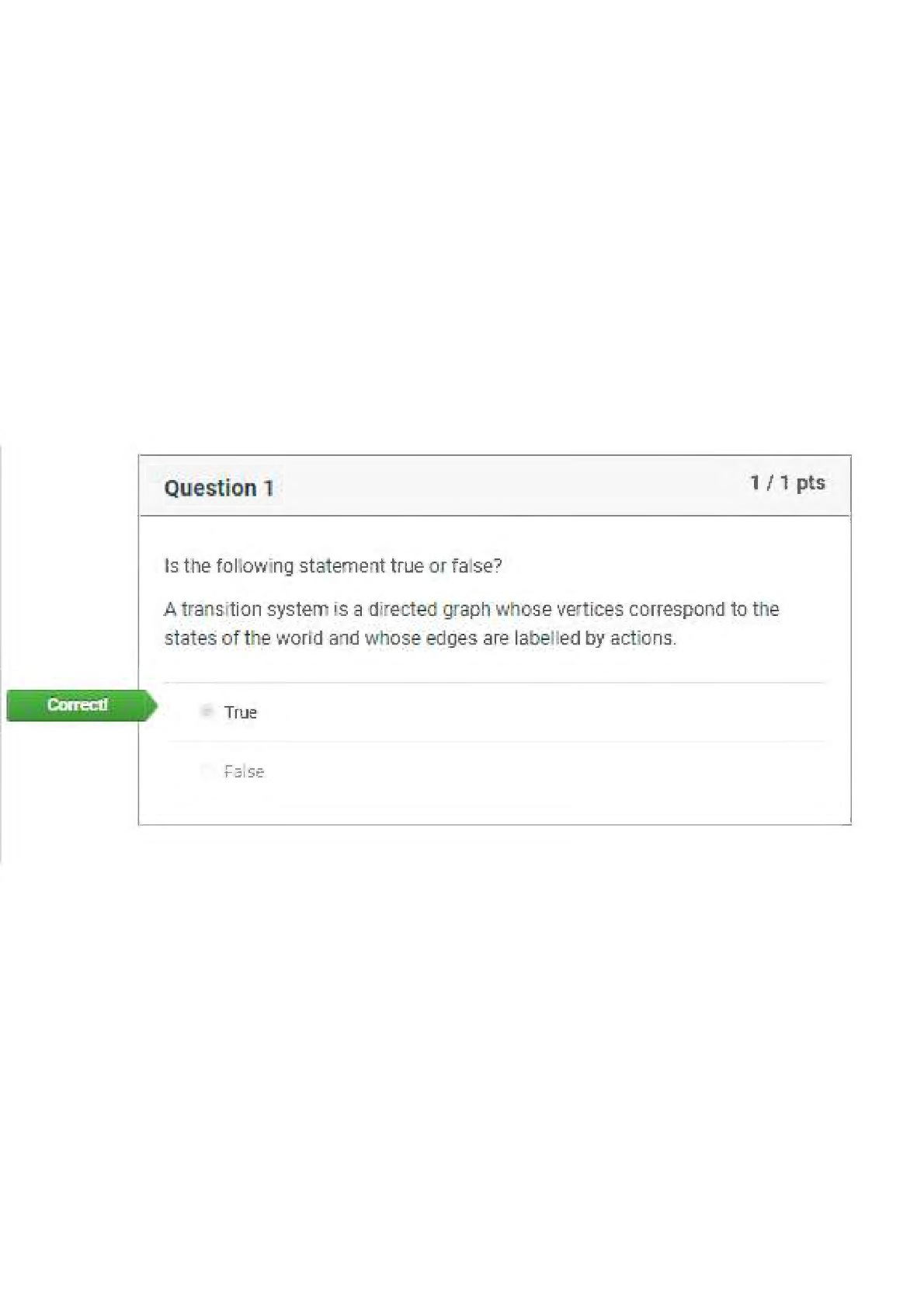2.[15] Two warring neighbours are separated by a field with wild berries. They agree to permit each other to enter the field to pick berries, but also need to ensure that only one of them is ever in the field at a time. After negotiation, they agree to the following protocol. When a one neighbour wants to enter the field, he raises a flag. If he sees his neighbour’s flag, he does not enter but lowers his flag and tries again. If he does not see his neighbour’s flag, he enters the field and picks berries. He lowers his flag after leaving the field. a.[8] Model this algorithm for two neighbours n1 and n2. Specified the required safety properties for the field and check that it does indeed ensure mutually exclusive access. Specify the required progress properties for the neighbours such that they both get to pick berries given a fair scheduling strategy. Are any adverse circumstances in which neighbours would not make progress? What if the neighbours are greedy? Page 2 of 5 b.[7] Model this algorithm for two neighbours using Petri nets (any kind). 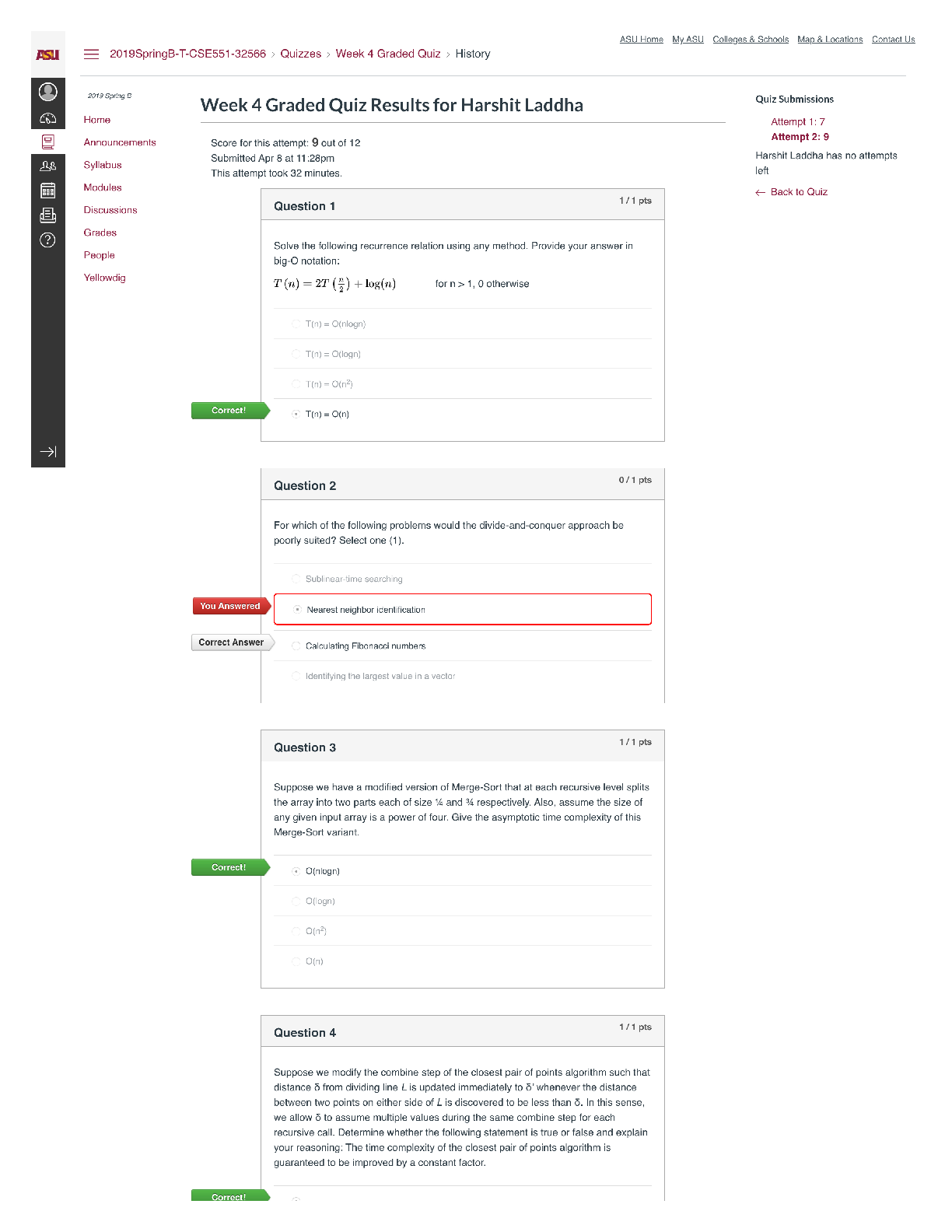3.[30] A cook puts burgers in a pot. A client checks if there is at least one burger in the pot, and if so, the client must take one. (a)[20] Assuming two clients, this can be modelled as (i)[12] Is there a trace belonging to process DS leading to an error state? If so, give the trace. (ii)[8] We wish a client to obtain exclusive access to the pot. That is, two clients cannot check the pot at the same time, and when a client checks, he/she must take a burger (if there is at least one). Show how to modify the given model such that this behaviour is ensured. (b)[10] Provide a solution with any kind of Petri nets. Note that the cook cannot put a burger in a full pot. [Show More]

Last updated: 2 years ago

Preview 1 out of 5 pages

Buy Now

Instant download

We Accept: