UNIT ASSIGNMENT
TRIGONOMETRY
Question 1 zadc
a). Find all solutions for sin (x )=√23
b). If sin (x )=1 3 and sec ( y)=54 , where 0≤ x ≤ π 2 and
0≤ y ≤ π 2 , evaluate the expression
sin (x-y) . Answers
a). x=π 3 +
...
UNIT ASSIGNMENT
TRIGONOMETRY
Question 1 zadc
a). Find all solutions for sin (x )=√23
b). If sin (x )=1 3 and sec ( y)=54 , where 0≤ x ≤ π 2 and
0≤ y ≤ π 2 , evaluate the expression
sin (x-y) . Answers
a). x=π 3 +2πn , 23π +2πn , where n∈Z
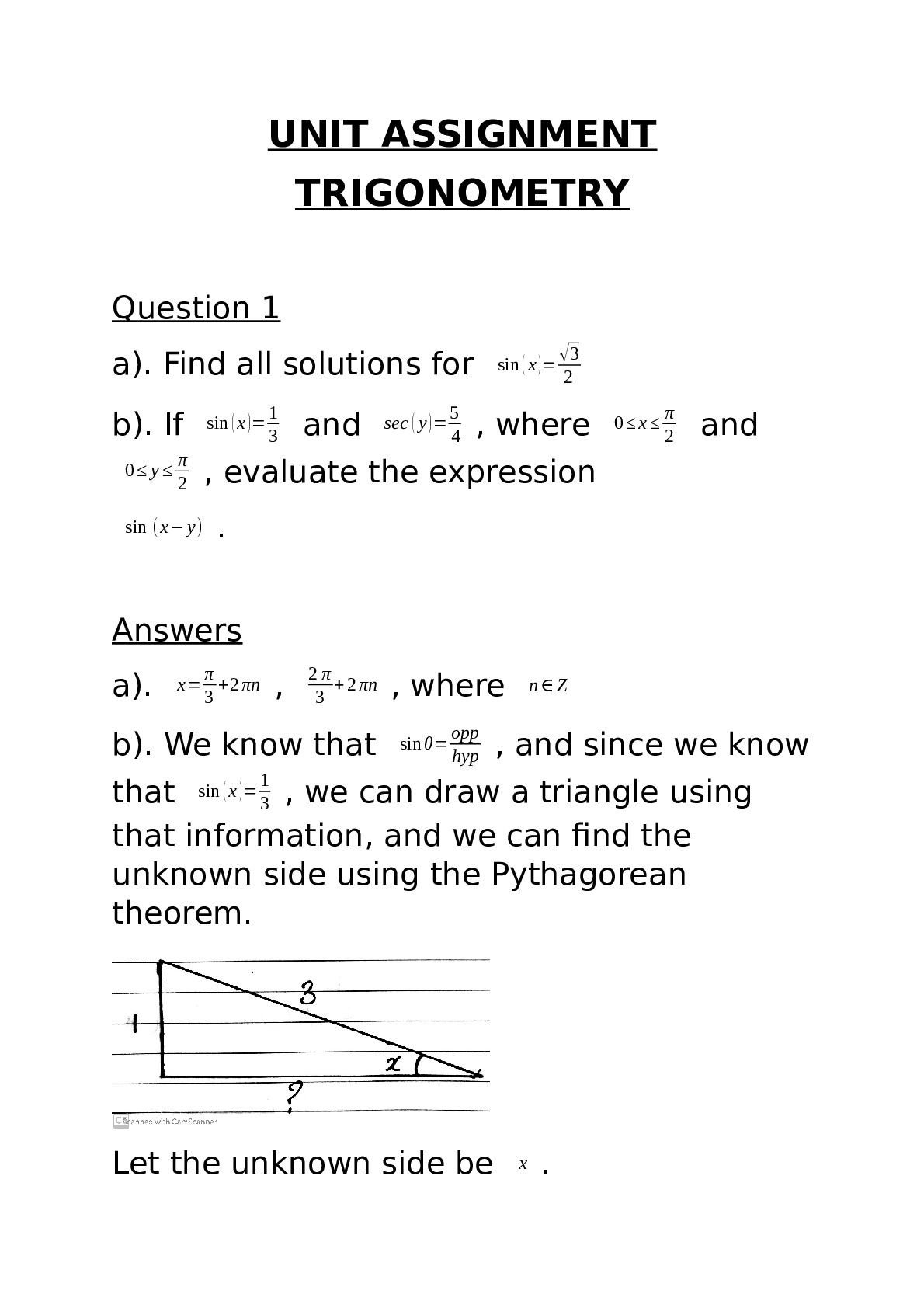
b). We know that sin θ=opp hyp , and since we know that sin (x )=1 3 , we can draw a triangle using that information, and we can find the unknown side using the Pythagorean theorem.
Let the unknown side be x .
x 2 +12=32 x 2 =9-1 x 2 =8 x=√8 x=2√2
Now that we know the length of the adjacent side, we can get the value of cos(x) , since cosθ= adj hyp , we know that cos ( x )= 23√2 .
Since sec ( y )= 5 4 , and since cosθ= sec 1 θ , we know that cos ( y )= 4 5 . Using the same steps as before, we can find the value of sin( y) , by finding the length of the opposite side. Let the opposite side be x . Using the Pythagorean theorem, we get:
x 2 +42=52 x 2 =25-16 x 2 =9 x=3
Now that we know the length of the opposite side, we can derive the value of sin ( y) , which is 3 5 .
Now let’s evaluate sin(x- y) . Using the angle difference formula, we get:
sin (x-y )=sin (x )cos ( y )-cos (x )sin ( y )
Substituting all the known values into the equation, we get:
sin (x-y )=(1 3 × 4 5)-(23√2 × 3 5)
¿ 4
15
- 2√2
5
¿ 4-6√2
15
Question 2
Solve for all values of x in the given intervals.
a). 2cos(x )+sin (2 x )=0 for 0≤ x ≤2 π
b). 2sin2(x)=1 for x∈R
c). tan2(x )-3=0 for x∈R
Answers a).
Combining all the solutions, we get x=π 2 , 32π .
b).
x=
π4
+πn , 3π
4
+πn where n∈Z .
x=
π3
+πn , 2π
3
+πn where n∈Z .
Question 3
Prove the following identities:
a). cos(x+ π 2)=-sin (x)
b). (sin (x )+cos(x ))2=1+sin (2 x) c). 2csc(2 x )=sec(x)csc (x)
d). sin sin((x x-+ yy))=tan tan((xx))-+tan tan((yy))
e). sec tan ((--tt))=-csc (t )
Answers a).
b).
c).
d).
e).
Question 4
Describe how to use both an equivalent trigonometric identity and a diagram to demonstrate that two trigonometric ratios are equivalent.
a). Use one of the following equivalent trigonometric expressions:
sin(θ+ 32π)=-cos(θ)
cos(θ+ 32π)=sin (θ)
tan(θ+ 32π)=-cot (θ)
sin(32π -θ)=-cos (θ )
cos(32π -θ)=-sin (θ )
tan(32π -θ)=cot(θ )
b). Using a diagram, demonstrate how the related angle formulas are true. Create an example to illustrate your findings in part a). (choose a value for θ and solve both sides to prove that they are equal.)
Answers
i). sin(θ+ 32π)=-cos(θ)
a). Let a be the LHS and b be the RHS of
the equation.
a=¿
sin(θ+ 32π)=¿
sin (θ)cos(32π)+cos(θ )sin(32π)=¿
sin (θ)×(0 )+cos (θ)×(-1)=¿
-cos(θ )=b a=b ∴ LHS=RHS
b). Let us look at the graphs of either side of the equation.
LHS sin(θ+ 32π)
This is what the graph of the base function, sin (θ) , looks like:
And this is what the graph of the function looks like after 3 π 2 has been added to the x
value:
As you can see the graph of the base function has been shifted to the left, by a value of 3 π 2 units.
RHS
-cos(θ )
This is what the graph of the base function, cos(θ ) , looks like:
And this is what the graph of -cos(θ ) looks
like:
As you can see, the graph has been reflected over the x -axis.
Now let us compare the graphs of both sides of the original equation.
When drawn on the same graph, you can see that they overlap. This proves that the two sides of the equation are indeed, equal.
ii). cos(θ+ 32π)=sin (θ)
a). Let a be the LHS and b be the RHS of
the equation.
a=¿
cos(θ+ 32π)=¿
cos(θ )cos(32π)-sin (θ)sin(32π )=¿
sin (θ )× (-1)=¿ -sin (θ)×(-1)=¿
sin (θ)=b a=b ∴ LHS=RHS
b). Let us look at the graphs of either side of the equation.
LHS
This is what the graph of the base function, cos(θ ) , looks like:
And this is what the graph of cos(θ+ 32π) looks like:
As you can see, the graph of the base function has been shifted to the left by a value of 3 π 2 units.
RHS
This is what the graph of the RHS of the equation, sin (θ) , looks like:
Let us compare the graphs of both sides of the equation.
When drawn on the same graph, we can see that they overlap. This means that both sides of the equation are equal.
iii). tan(θ+ 32π)=-cot (θ)
a). Let a be the LHS and b be the RHS of
the equation.
a=¿
tan(θ+ 32π)=¿
sin(θ+ 32π)
cos(θ+ 32π)
Looking back at the previous two examples,
we can substitute the values,
sin(θ+ 32π)
cos(θ+ 32π)=¿
-cos (θ) sin (θ) =¿
-cot (θ)=b a=b ∴ LHS=RHS
b). Let us look at the graphs of either side of the equation.
LHS tan(θ+ 32π)
This is what the graph of the base function, tan (θ ) , looks like:
And this is what the graph of tan(θ+ 32π) looks like:
As you can see, the graph of the base function, has been shifted to the left by a value of 3 π 2 .
RHS
This is what the graph of the base function, cot (θ) looks like:
And this is what the graph of -cot (θ) looks
like:
As you can see, the base function, cot (θ) , has
been reflected over the x -axis.
Now let’s compare the graphs of both sides of the equation.
When drawn on the same graph, we can see that they overlap. This proves that both sides of the equation are equal.
iv). sin(32π -θ)=-cos (θ)
a). Let a be the LHS and b be the RHS of
the equation.
a=¿
sin(32π -θ)=¿
sin(32π )cos (θ)-cos(32π)sin (θ )=¿
(-1)× cos (θ )-(0) sin (θ)=¿ -cos(θ )=b
a=b
∴ LHS=RHS
b). Let us look at graphs of either side of the equation.
LHS
This is what the graph of the base function, sin (θ) , looks like:
And this is what the graph of sin(32π -θ) looks
like:
As you can see, the graph has been reflected over the x -axis, and it has been translated left by a value of 32π units. RHS
This is what the base function, cos (θ) , looks like:
And this is what the graph of -cos (θ ) looks
like:
Let us compare the graphs of both sides of the original equation.
When drawn on the same graph, we can see that they overlap. This means both sides of the equation are equal.
v). cos(32π -θ)=-sin (θ )
a). Let a be the LHS and b be the RHS of
the equation.
a=¿
cos(32π -θ)=¿
cos(32π)cos(θ )+sin(32π)sin (θ)=¿
(0) cos (θ )+(-1 )sin (θ )=¿
-sin (θ)=b
a=b ∴ LHS=RHS
b). Let us compare the graphs of both sides of the equation.
LHS
This is what the base function, cos (θ) , looks like:
And this is what the graph of cos(32π -θ) looks
like:
As you can see, the graph has been reflected over the x -axis and has been shifted left by a value of 32π units. RHS
This is what the graph of the base function, sin (θ) , looks like:
This is what the graph of -sin (θ) looks like:
Now let’s compare the graphs of both sides of the original equation:
When drawn on the same graph, you can see that they overlap. This means that both sides of the equation are equal.
vi). tan(32π -θ)=cot(θ )
a). Let a be the LHS and b be the RHS of
the equation.
a=¿
tan(32π -θ)=¿
sin(32π -θ)
cos(32π -θ)
Looking back at the previous two examples, we can substitute the values.
sin(32π -θ)
cos(32π -θ)=¿
-cos(θ) -sin (θ) =¿
1
tan (θ)=¿
cot (θ)=b a=b ∴ LHS=RHS
b). Let’s compare the graphs of both sides of the equation.
LHS
This is what the graph of the base function, tan (θ ) , looks like:
And this is what the graph of tan(32π -θ) looks
like:
We can see that the graph has been reflected over the x -axis and it has been shifted to the left by a value of 32π .
This is what the graph of cot (θ) looks like:
Now let us compare the graphs of both sides of the equation.
When drawn on the same graph, we can see that they overlap. This means that both sides of the equation are equal
[Show More]