Georgia Institute of Technology (GT) _ CSE 6220 Intro to High Performance Computing - Intro to HPC Final Exam A Solutions.

Document Content and Description Below

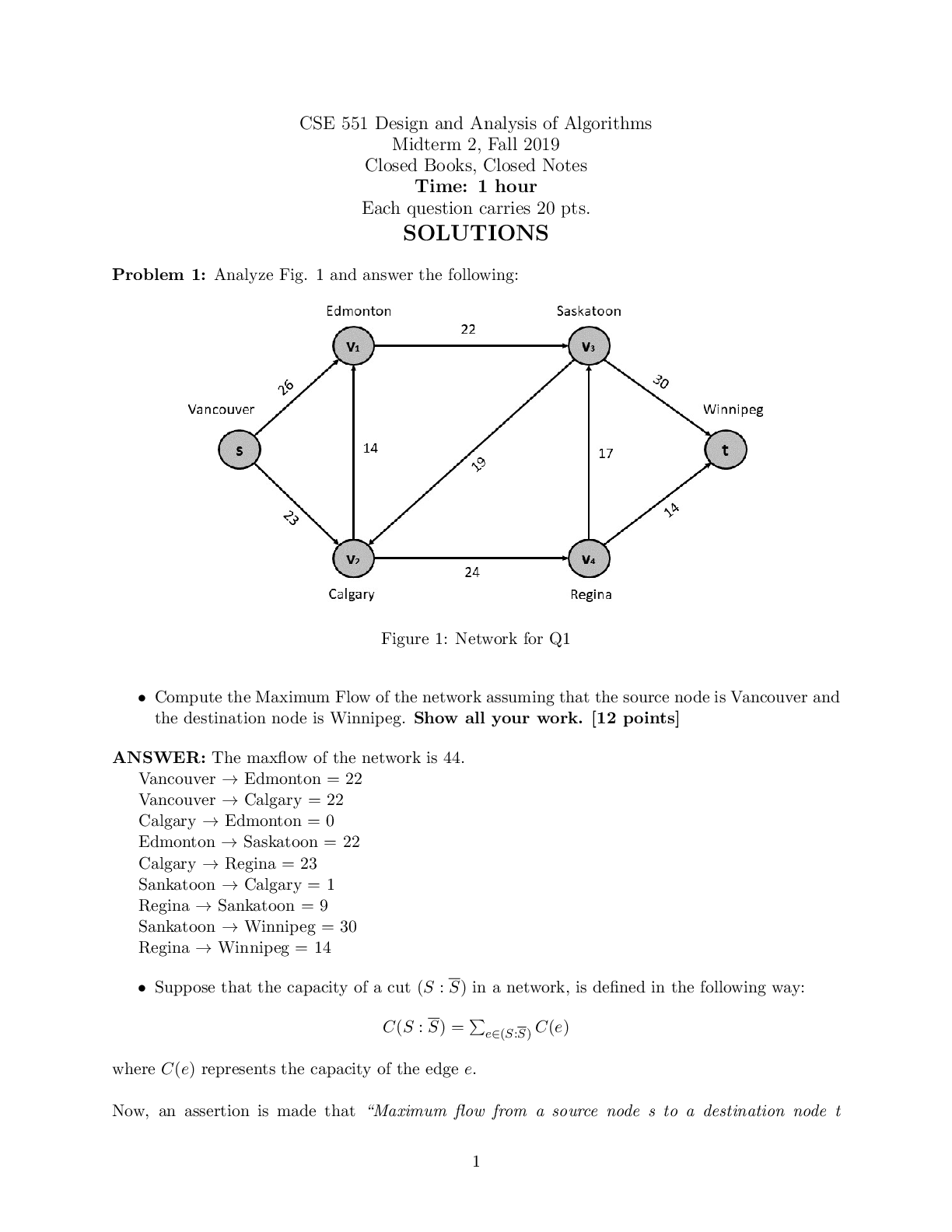
CSE 6220 (OMS CS): Intro to HPC Final Exam A Apr 30–May 4 Question 1 (10 points) Funnel Sort Consider a machine with a simple two-level memory system. We have been tasked with the unenvious job of ... sorting an array of integers using Funnel Sort. Assuming the standard Funnel data structure, i.e., where a K-Funnel will output K3 elements, please answer the following questions: (a) (4 points) What is the size of the largest Funnel used to sort arrays of the following sizes? 1. 224 2. 104 (b) (4 points) Let us assume that a 4-Funnel is able to fit in cache along with 1 block from each of its input lists. Let’s call this the J-Funnel. In the amortized analysis of Funnel Sort we only charge elements an “IO cost” when they enter buffers of any ≥ J-Funnel. How many such buffers would be crossed by each element in the final merge step for the largest K-Funnels from the previous part?\ (c) (2 points) The figure below represents an intermediate state during the process of merging via a 16-Funnel. List out the order of buffers which will be filled completely before another element is pushed into the output buffer. Assume that left funnels are called first in case both right and left buffers are empty. Question 2 (10 points) Back-of-the-envelope Suppose you are given a distributed algorithm that sends m messages of length l and does c units of computation (flops, for example). The latency of the system is α and the bandwidth is β. Also the cost of a unit of computation is γ. (a) (2 points) Derive an expression for the running time of the algorithm assuming that 60% of the computation can be overlapped with communication. (b) (2 points) Suppose that all the computation can be overlapped with communication derive an expression for the idle time (i.e. the time spent by the compute nodes waiting for communication operations to finish). c) (2 points) Now suppose that the latency is fixed and the bandwidth can be changed. by what factor would the bandwidth need to increase to ensure that the utilization of the compute nodes is maximized (i.e. no idle time)? (c) (2 points) For the next two parts assume that there is no overlap between computation and communication. Suppose we could trade u messages for 4cu2 units of computation. How many messages should we trade to minimize run time? Assume that u takes on real number values for this question. e) (2 points) In the analysis of the previous part, what is the maximum value of u for which we can obtain some improvement in running time over the case u = 0? Suppose for a real implementation this maximum value of u came out to be 0:573, what would you conclude about the feasibility of trading computation for communication? Question 3 (10 points) Implementing MPI BARRIER with a Tag A call to MPI BARRIER blocks a process until all processes in the communicator have called this routine. Recall that MPI does not require these processes to reach the same call (e.g., program call site), just any call to MPI BARRIER. Suppose you wish to distinguish between different calls to MPI BARRIER. To overcome above limitation MPI BARRIER, we propose another barrier routine MPI BARRIER TAG that takes additional input “tag” to differentiate between different calls to MPI BARRIER. (a) (7 points) Give a pseudo-code for MPI BARRIER TAG function that only uses MPI SEND, MPI RECV, MPI COMM RANK, and MPI COMM SIZE. You may not use the MPI-provided MPI BARRIER directly. Your function should take the communicator and identifying tag as an input. [Show More]

Last updated: 2 years ago

Preview 1 out of 10 pages