FN 3250 Finance _ Chapter 5 Extra Problems - KEY: Why did the Mets agree to such a deal? Darren Rovell of ESPN explains: “The Mets have never really talked about the deal, but it is well known that their owners, the Wilpons, had many accounts with investor Bernie Madoff.

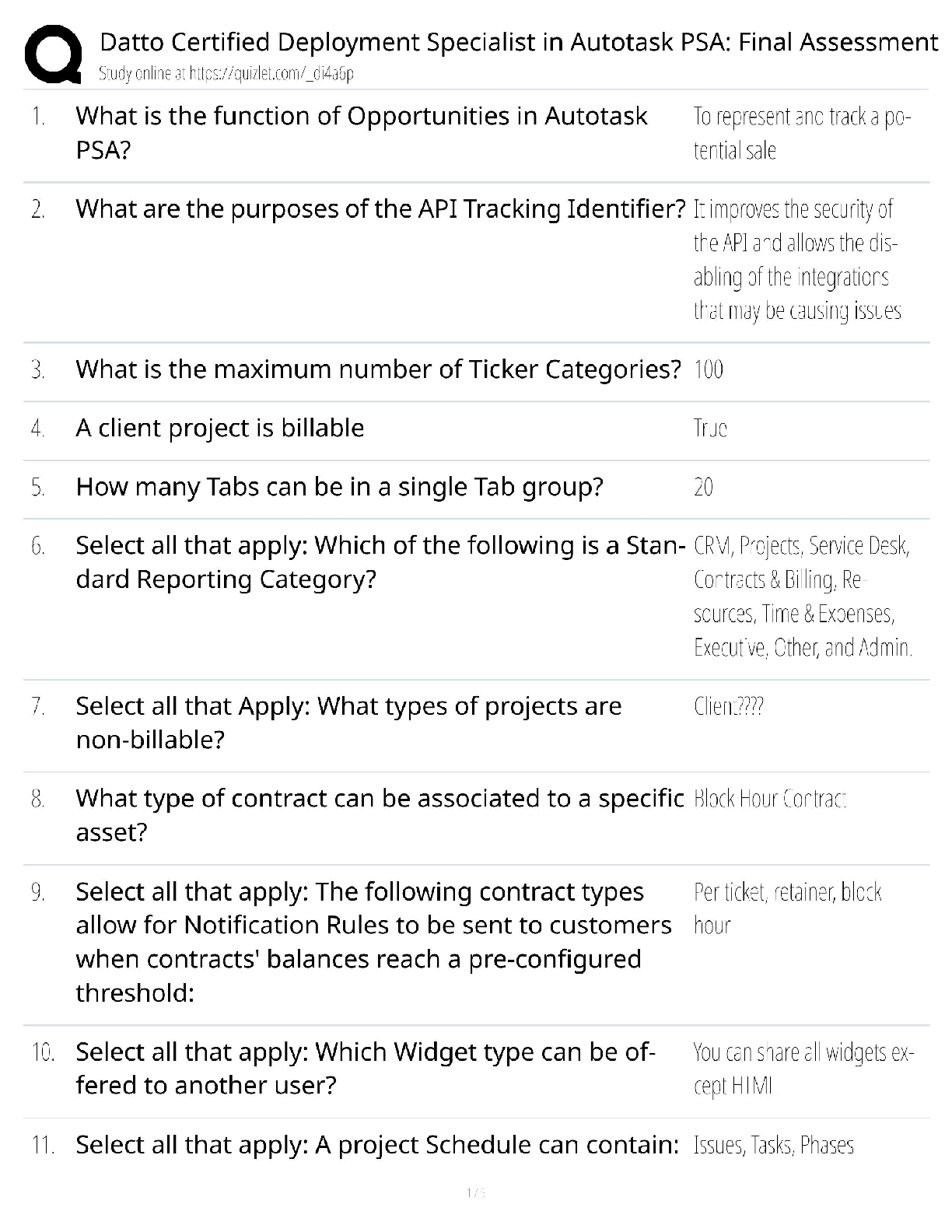
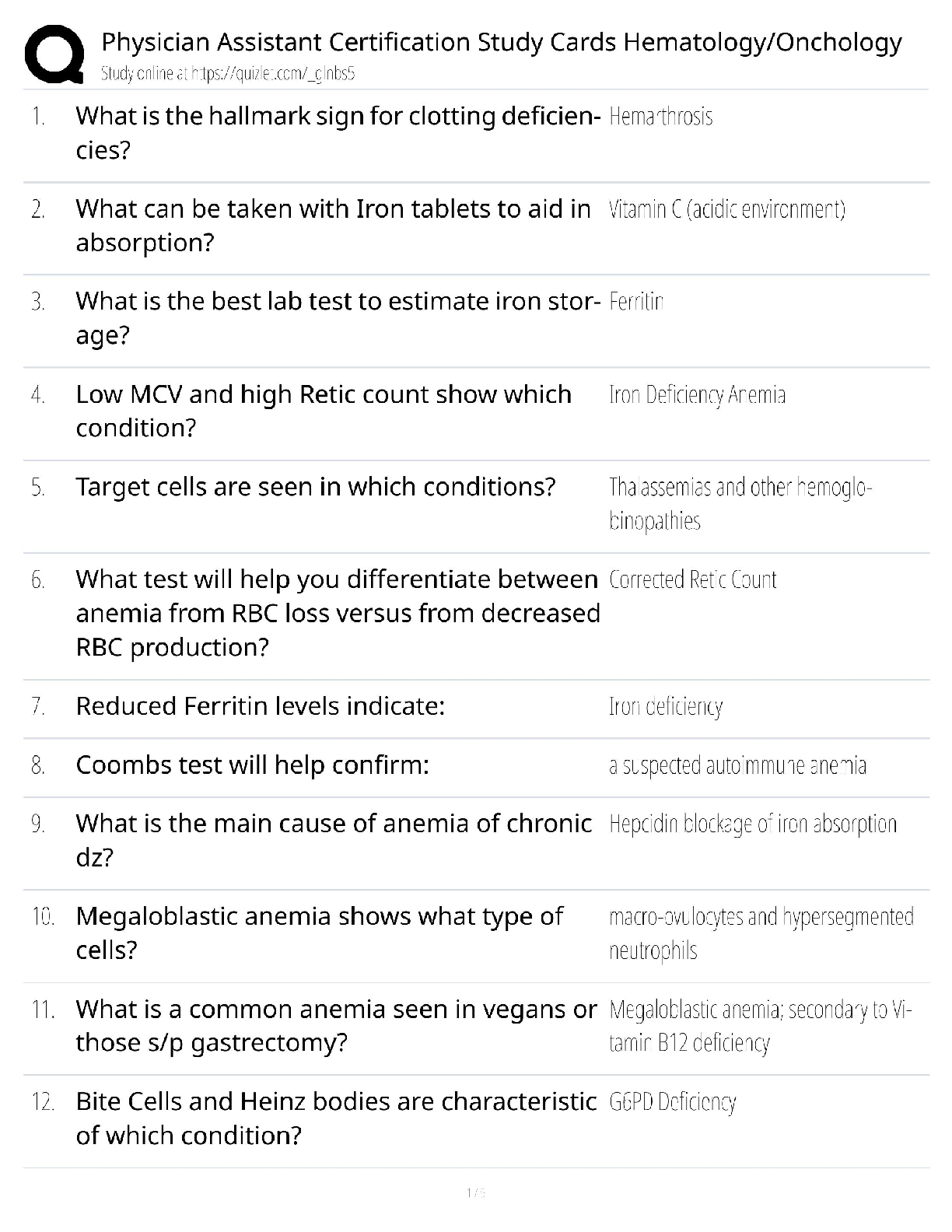
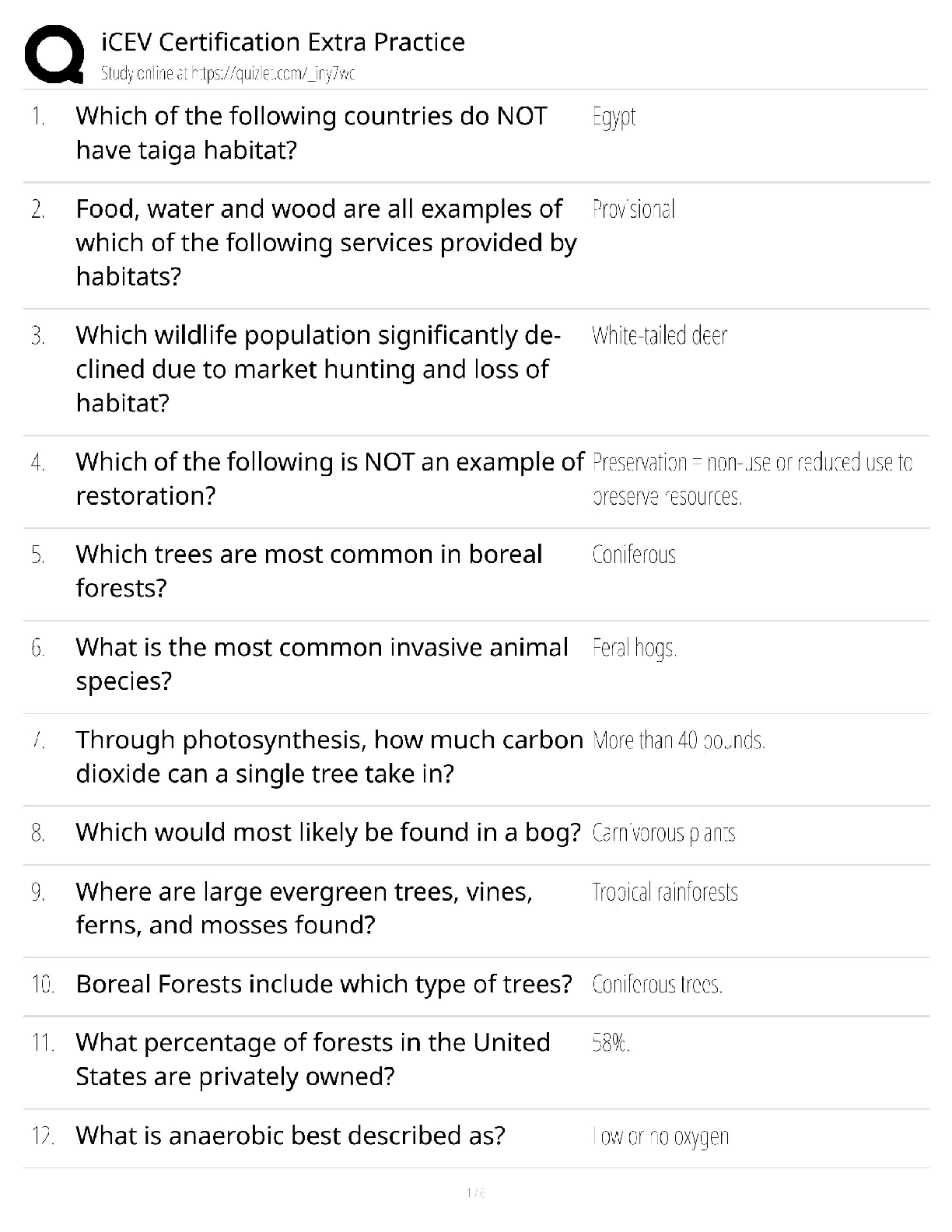
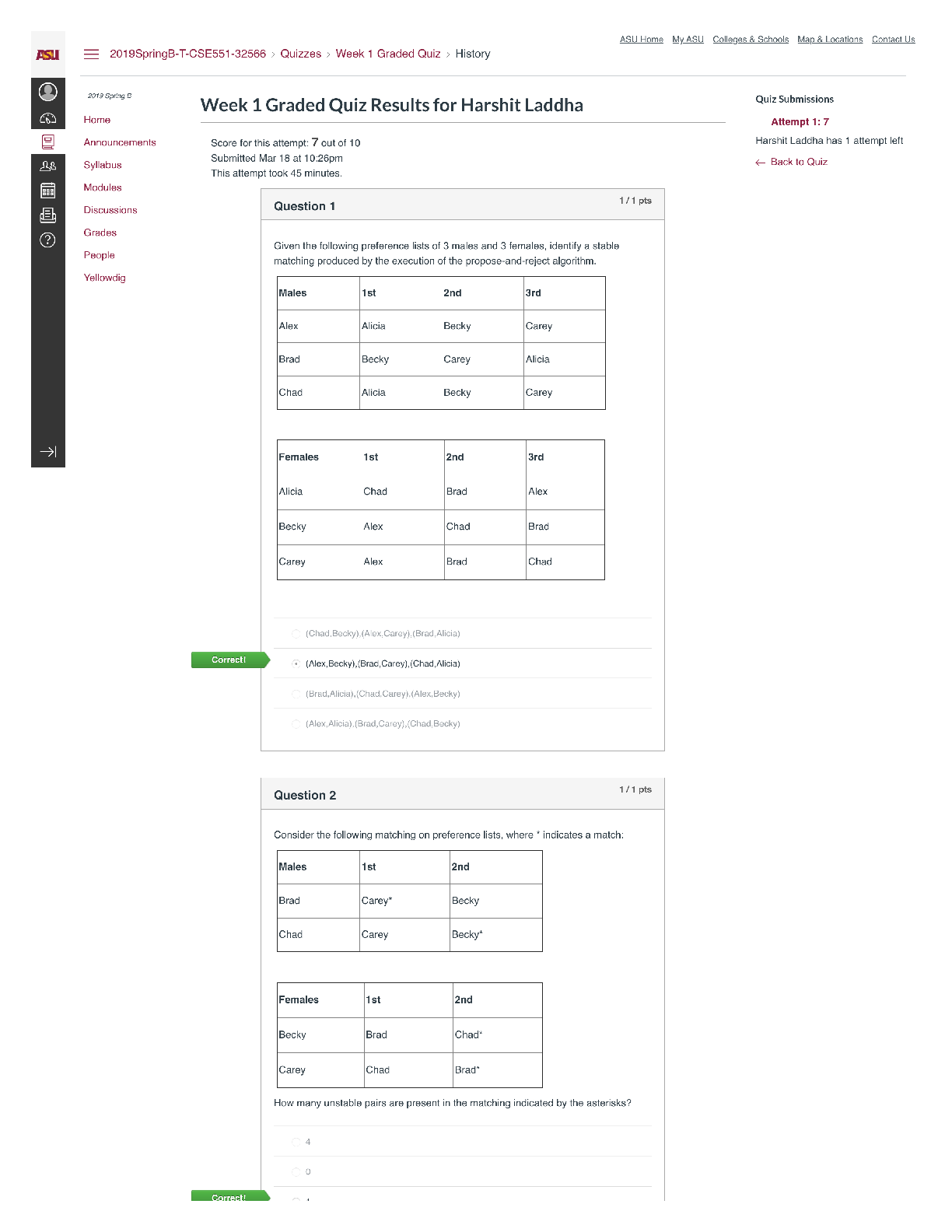
Chapter 5 Extra Problems - KEY For all problems in which you use your financial calculator, identify all inputs entered. 1. Bobby Bonilla was a professional baseball player whom the New York Mets had under contract th ...

Chapter 5 Extra Problems - KEY For all problems in which you use your financial calculator, identify all inputs entered. 1. Bobby Bonilla was a professional baseball player whom the New York Mets had under contract through the end of the 2000 season. However, the Mets decided to cut Bonilla from the team after the 1999 season. Instead of paying Bonilla his guaranteed salary of $5,900,000 for the 2000 season, the Mets offered him a “deferred-money deal.” The Mets agreed to pay Bonilla an 8% return on the $5.9 million with payments drawing this sum down beginning in 2011. Starting on July 1, 2011, the Mets have to pay Bonilla $1,193,248.20 every July 1 through the year 2035. Why did the Mets agree to such a deal? Darren Rovell of ESPN explains: “The Mets have never really talked about the deal, but it is well known that their owners, the Wilpons, had many accounts with investor Bernie Madoff. Madoff was returning 12 to 15 percent a year in what we now know were fictional returns. So deferring deals wasn't a problem because the payout would occur years later and the interest rate would be lower than the money they were (fictionally) getting back from Madoff. To see the deal as the Mets would have seen it, let's say the Wilpons put $5.9 million into a Madoff account in 2000 and got a conservative (by Madoff standards) 10 percent annual return. By 2011, when they would have to pay Bonilla for the first time, they would have already grown their pot to $(see ‘a’ below) million. Even with paying off Bonilla every year, they would wind up with a $49 million profit on the deal. Of course, the Madoff returns weren't real, which complicates this hindsight.” Despite the seemingly solid financial decision given the facts at the time, many baseball fans celebrate July 1 as ‘Bobby Bonilla Day’ and joke about the Mets’ plight. As students of finance, let’s dig into the numbers a bit more before passing judgment on this deal. a. Fill in the blank above… If $5,900,000 was invested in 2000 and earned 10% per year, how much would the Mets have in 2011? Calculate the net present value of Bonilla’s payouts as of July 1, 2011 using discount rates of 5%, 8%, and 11%. (i.e. what was the NPV of the payments Bonilla would receive?) Note: Since the first payment occurred on July 1, 2011, use BGN mode where appropriate. c. As of July 1, 2011, what was the present value of Bonilla’s 5th payment? 15th payment? 25th payment? Use a discount rate of 8% for all calculations. d. Is it fair to say the Mets turned a $5.9 million dollar payment into nearly $30 million in payments over 25 years? 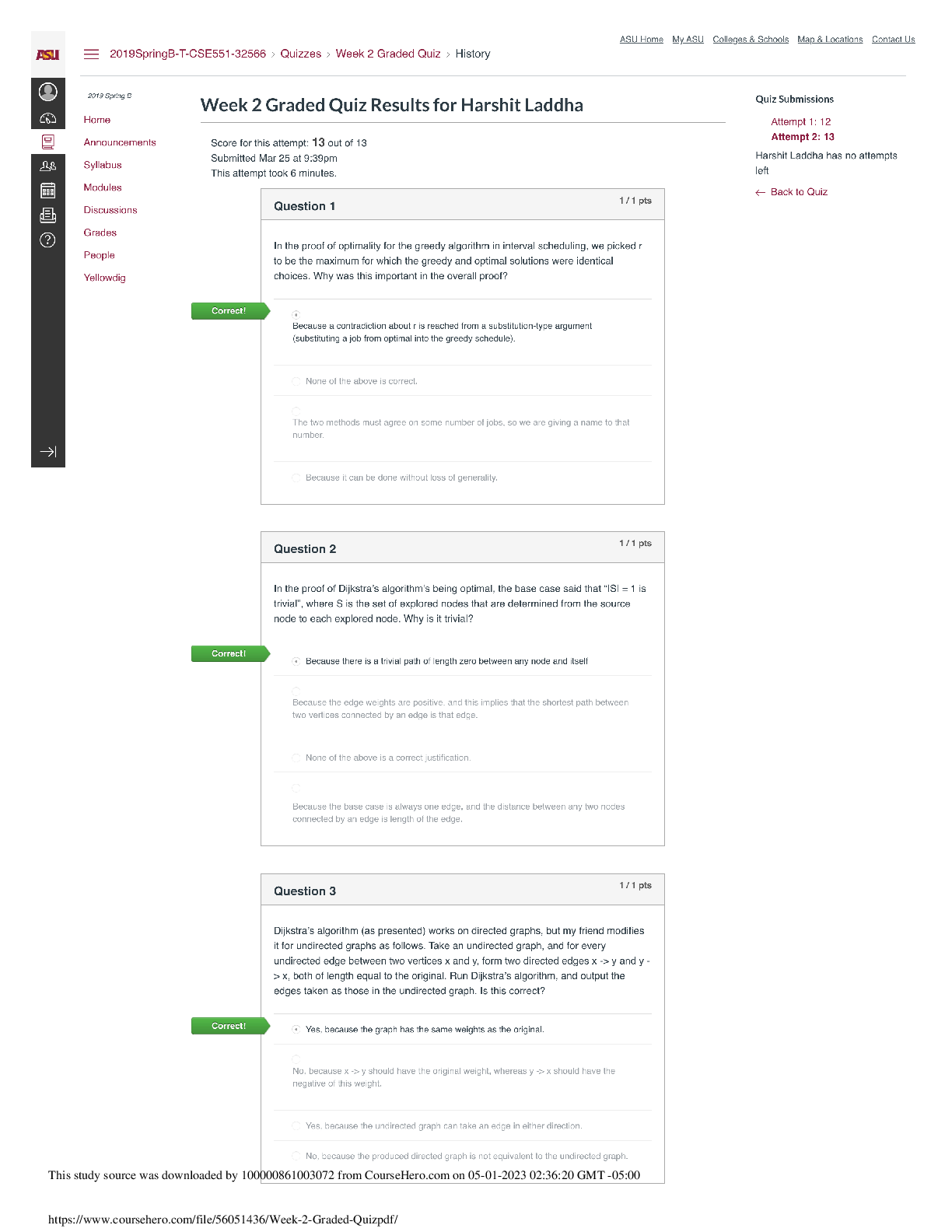2. You decide to spend $3,600 on new furniture at Nebraska Furniture Mart in part because they are offering 0% financing for 36 months. What is the present value of these payments discounted at 6%? 3. McDonald’s periodically runs a Monopoly promotion that claims to pay winners $1,000,000. However, that million dollars is actually paid through twenty annual payments of $50,000. a. What is the present value of this supposed million-dollar prize with a discount rate of 5%? 8%? Assume the payments occur at the end of the year. b. Calculate the net future value of the Monopoly payout using discount rates of 5%, 8%, and 11%. (i.e. what was the NFV of the payments a winner would receive?) c. As of the first payment date, what is the future value of the Monopoly payout’s 1st payment? 8th payment? 15th payment? Use a discount rate of 8% for all calculations. 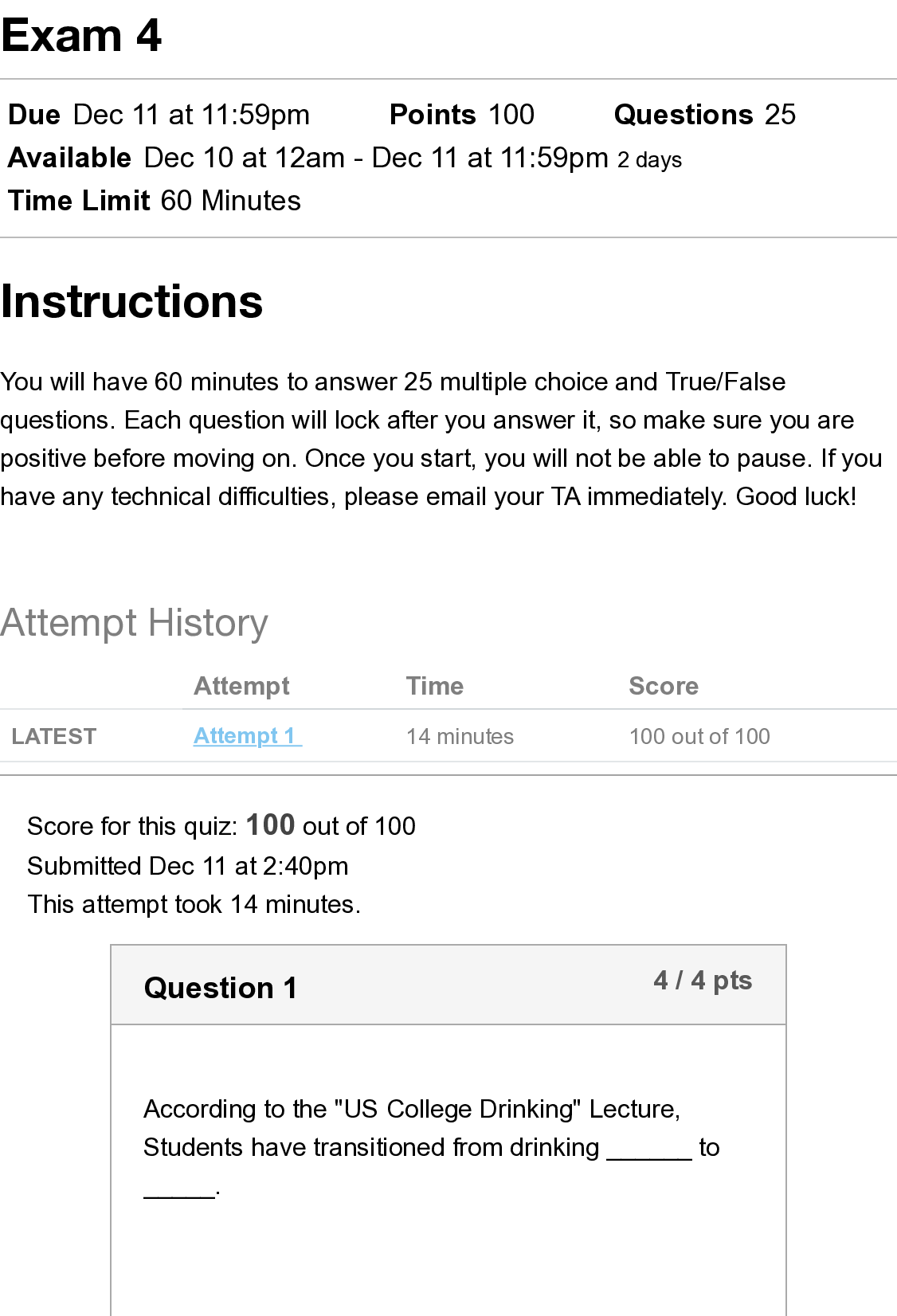4. Consider a $200,000 30-year mortgage with a 4.5% interest rate. a. What is the monthly payment on this loan? b. How much of the first month’s payment is interest? c. How much of the second month’s payment pays down the principal? d. Assume the borrower receives an inheritance of $50,000 shortly after the loan begins. If the borrower put this entire $50,000 toward the loan’s principal after the first payment but before the second payment, how much of the second month’s payment would go toward principal? e. Continuing from ‘d’, how much faster will the loan be paid off? How much interest will you save over the life of the loan? Note: Assume no extra principal payments beyond the initial $50,000 are made for the life of the loan. f. Starting fresh… If the borrower instead chose to take out a 15-year mortgage at 3.75%, how much would they save on interest over the life of the loan? Assume the borrower makes no extra principal payments in either scenario.