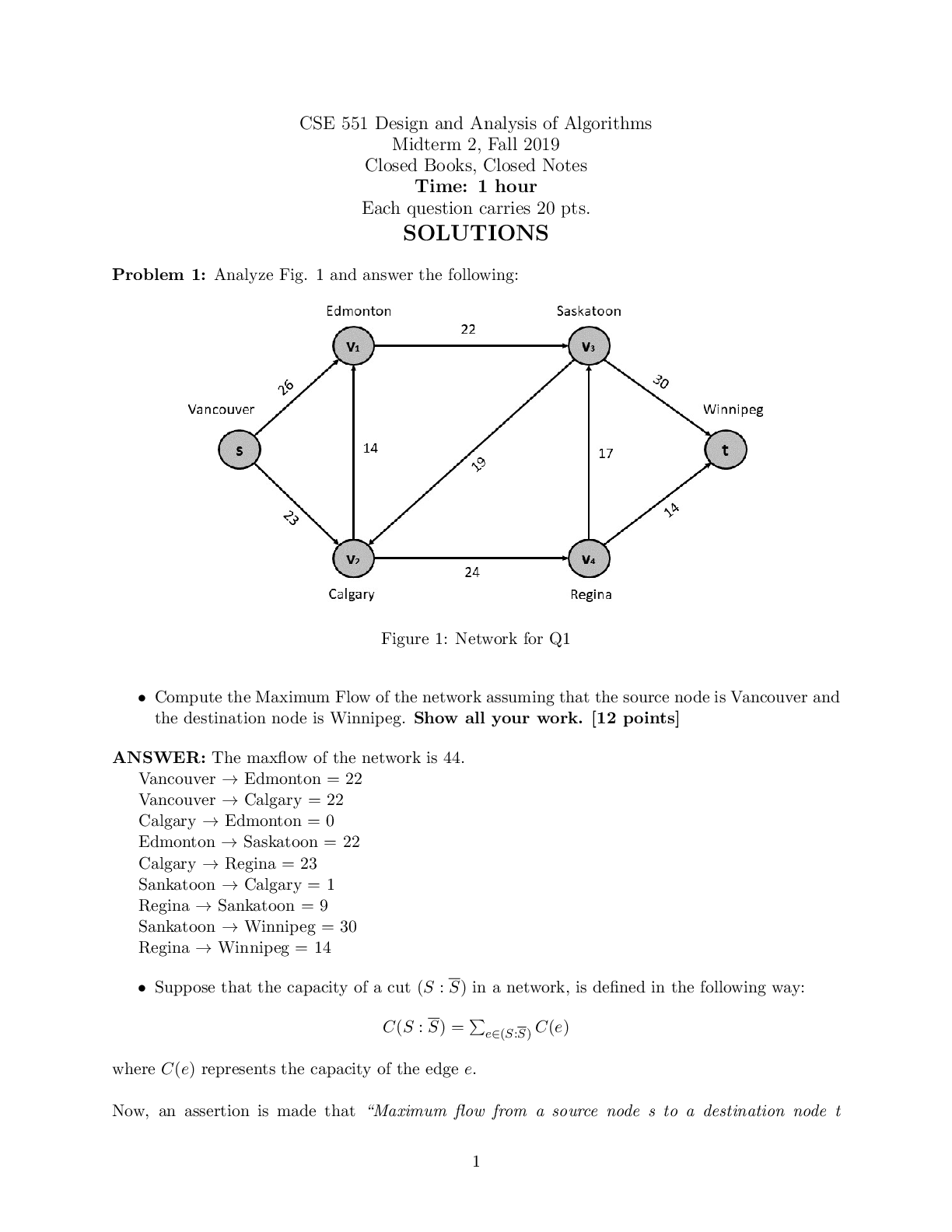
STAT 361 Data Analysis - Yale University WORKSHEET 3.7: STATISTICAL THINKING IN PYTHONWrite codes in Jupyter as required by the problems. Copy the code and output (as screen grab or screen shot) and paste them here.
1 D
...
STAT 361 Data Analysis - Yale University WORKSHEET 3.7: STATISTICAL THINKING IN PYTHONWrite codes in Jupyter as required by the problems. Copy the code and output (as screen grab or screen shot) and paste them here.
1 Date:
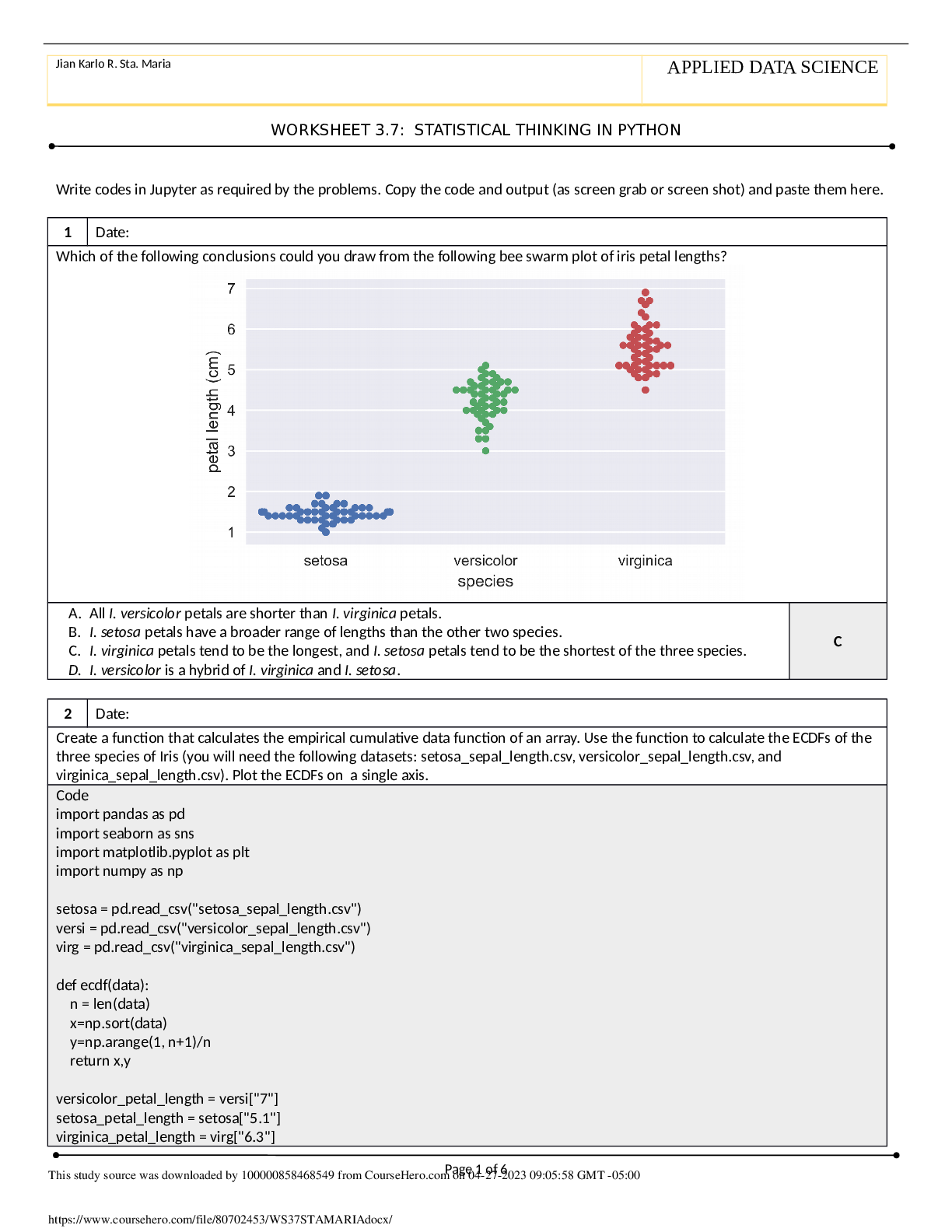
Which of the following conclusions could you draw from the following bee swarm plot of iris petal lengths?
A. All I. versicolor petals are shorter than I. virginica petals.
B. I. setosa petals have a broader range of lengths than the other two species.
C. I. virginica petals tend to be the longest, and I. setosa petals tend to be the shortest of the three species.
D. I. versicolor is a hybrid of I. virginica and I. setosa.
C
2 Date:
Create a function that calculates the empirical cumulative data function of an array. Use the function to calculate the ECDFs of the
three species of Iris (you will need the following datasets: setosa_sepal_length.csv, versicolor_sepal_length.csv, and
virginica_sepal_length.csv). Plot the ECDFs on a single axis.
Code
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
setosa = pd.read_csv("setosa_sepal_length.csv")
versi = pd.read_csv("versicolor_sepal_length.csv")
virg = pd.read_csv("virginica_sepal_length.csv")
def ecdf(data):
n = len(data)
x=np.sort(data)
y=np.arange(1, n+1)/n
return x,y
versicolor_petal_length = versi["7"]
setosa_petal_length = setosa["5.1"]
virginica_petal_length = virg["6.3"]
Page 1 of 6
This study source was downloaded by 100000858468549 from CourseHero.com on 04-27-2023 09:05:58 GMT -05:00
https://www.coursehero.com/file/80702453/WS37STAMARIAdocx/Jian Karlo R. Sta. Maria APPLIED DATA SCIENCE
WORKSHEET 3.7: STATISTICAL THINKING IN PYTHON
x_set, y_set = ecdf(setosa_petal_length)
x_vir, y_vir = ecdf(virginica_petal_length)
x_vers, y_vers = ecdf(versicolor_petal_length)
plt.plot(x_set, y_set, marker='.', linestyle='none')
plt.plot(x_vers, y_vers, marker='.', linestyle='none')
plt.plot(x_vir, y_vir, marker='.', linestyle='none')
plt.legend(('setosa', 'versicolor', 'virginica'), loc='lower right')
plt.xlabel('sepal length (cm)')
plt.ylabel('ECDF')
plt.show()
Output
3 Date:
Which of the following statements is true about means and medians?
A. An outlier can significantly affect the value of both the mean and the median.
B. An outlier can significantly affect the value of the mean, but not the median.
C. Means and medians are in general both robust to outliers.
D. The mean and median are equal if there is an odd number of data points.
B
4 Date:
Without plotting the data, determine the 25th, 50th and 75th percentiles of the three iris species.
Code
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
setosa = pd.read_csv("setosa_sepal_length.csv")
Page 2 of 6
This study source was downloaded by 100000858468549 from CourseHero.com on 04-27-2023 09:05:58 GMT -05:00
https://www.coursehero.com/file/80702453/WS37STAMARIAdocx/Jian Karlo R. Sta. Maria APPLIED DATA SCIENCE
WORKSHEET 3.7: STATISTICAL THINKING IN PYTHON
versi = pd.read_csv("versicolor_sepal_length.csv")
virg = pd.read_csv("virginica_sepal_length.csv")
versicolor = np.percentile(versi["7"], [25, 50, 75])
setosa = np.percentile(setosa["5.1"], [25, 50, 75])
virginica = np.percentile(virg["6.3"], [25, 50, 75])
print("Versicolor: ", versicolor)
print("Setosa: ", setosa)
print("Virginica: ", virginica)
Output
Versicolor: [5.6 5.9 6.3]
Setosa: [4.8 5. 5.2]
Virginica: [6.2 6.5 6.9]
5 Date:
Let’s say a bank made 100 mortgage loans. It is possible that anywhere between 0 and 100 of the loans will be defaulted upon. We
would like to know the probability of getting a given number of defaults, given that the probability of a default is 0.05. Draw
10,000 samples of this binomial distribution and plot the CDF using our ecdf function. Do not forget to use
np.random.seed(42).
[Show More]