RSK 4805: Market Risk Question and Answer Bank

Document Content and Description Below

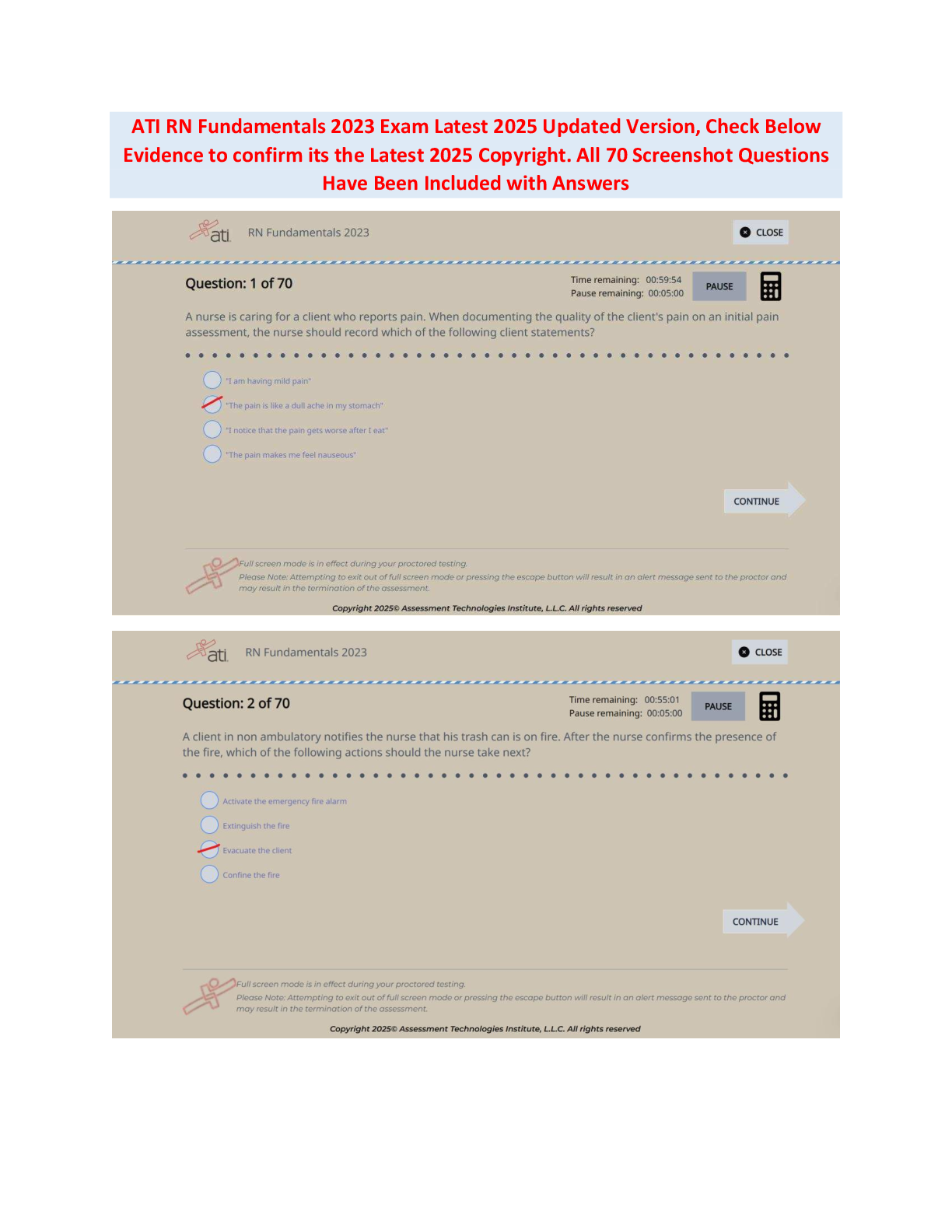
RSK 4805: Market Risk Question and Answer Bank 1.1.1 Final Exam | May/June 2016 | Question 2.2 Consider a two-period binomial model in which a stock currently trades at a price of R160. The stock pr ... ice can go up or down by 10% each period. The risk-free rate is 7.2%. Calculate the price of the European call and put options expiring in two periods with an exercise price of R145 and R160 respectively. [7 marks] 1.1.2 Final Exam | May/June 2016 | Question 2.4 Complete the table below by indicating what the influence on the value/price of the options will be if the variable increases or decreases as indicated. [3 marks] Variable State Call option value Put option value Interest rate Increase Higher Lower Spot price Increase Higher . . . Strike price Increase . . . Higher Volatility Decrease . . . Lower 1.1.3 Final Exam | January/February 2016 | Question 2.3 Consider a share that is currently priced at R100. The stock can increase by 25% and decrease by 20% over the next period. Assume a call option with an exercise price of R100 and a risk free rate of 7%. Calculate the hedge ratio and value of the call option using a one-period binomial model. [4 marks] 1.1.4 Final Exam | May/June 2015 | Question 2.1 Consider a European option on a non-dividend paying share when the share price is R48, the strike price is R50, the time to maturity is 3 months and the risk-free interest rate is 12% per annum. Calculate the lower and upper bound for the option price. [4 marks] 1.1.5 Final Exam | May/June 2015 | Question 2.4 Consider a two-period binomial model in which the stock currently trades at $50. The stock price can go up 20% or down 20% in each period. The risk-free rate is 7% per year. A put option on this stock expiring in 1 2 1 Option Contracts and Risk Application Strategies two periods has an exercise price of $55. Calculate the number of units that would be needed at time 0 in the binomial tree to construct a risk-free hedge. Use 10,000 puts. [4 marks] 1.1.6 Final Exam | January/February 2015 | Question 2.1 Consider a European call option on a non-dividend paying share when the share price is R61, the strike price is R60, the time to maturity is 6 months and the risk-free interest rate is 12% per annum. Calculate the lower bound for the option price. [2 marks] 1.1.7 Final Exam | January/February 2015 | Question 2.5 Consider a two-period binomial model in which a share currently trades at a price of R200. The share price can go up or down by 10% each period. The risk-free rate is 7%. Calculate the price of an American put option expiring in two periods with a R220 strike. [5 marks] 1.1.8 Final Exam | May/June 2014 | Question 2.1 Consider a two-period binomial model in which a share currently trades at a price of R150. The share price can go up or down by 10% each period. The risk-free rate is 7%. 1. Calculate the price of a European call option expiring in two periods with an exercise price of R125. [3 marks] 2. Calculate the price of an American put option expiring in two periods with a strike price of R155. [3 marks] 1.1.9 Final Exam | May/June 2013 | Question 2.1 Consider that you have a share currently priced at $50, and a two-period European call option is available with a strike price of $45. The size of an up-move is 25%, and the size of a down-move is 20%. The risk-free rate per period is 7%. Compute the value of the call option using a two-period binomial model. [7 marks] 1.1.10 Final Exam | January/February 2013 | Question 2.1 Consider a binomial model in which a share currently trades at a price of $85. The share price is expected to increase by 12% and decrease by 7% each period. The risk-free rate is 5.5%. Calculate the price of a European put option expiring in the next period with an exercise price of $90. [5 marks] 1.2 Solutions 3 1.2 Solutions 1.2.1 Final Exam | May/June 2016 | Question 2.2 First, we find the share prices in the binomial tree. • S = R160 • u = 1.1 • d = 0.9 • S+ = Su = R160 × 1.1 = R176 • S− = Sd = R160 × 0.9 = R144 • S++ = S+u = R176 × 1.1 = R193.60 • S+− = S+d = R176 × 0.9 = R158.40 • S−− = S−d = R144 × 0.9 = R129.60 The risk-neutral probability, π, is: π = (1 + r) −d = (1 + 7.2%) − 0.9 = 0.86 (1.1) And: [Show More]

Last updated: 2 years ago

Preview 1 out of 13 pages