Questions and Answers > George Mason University - ECE 301HW11 Solutions

Document Content and Description Below

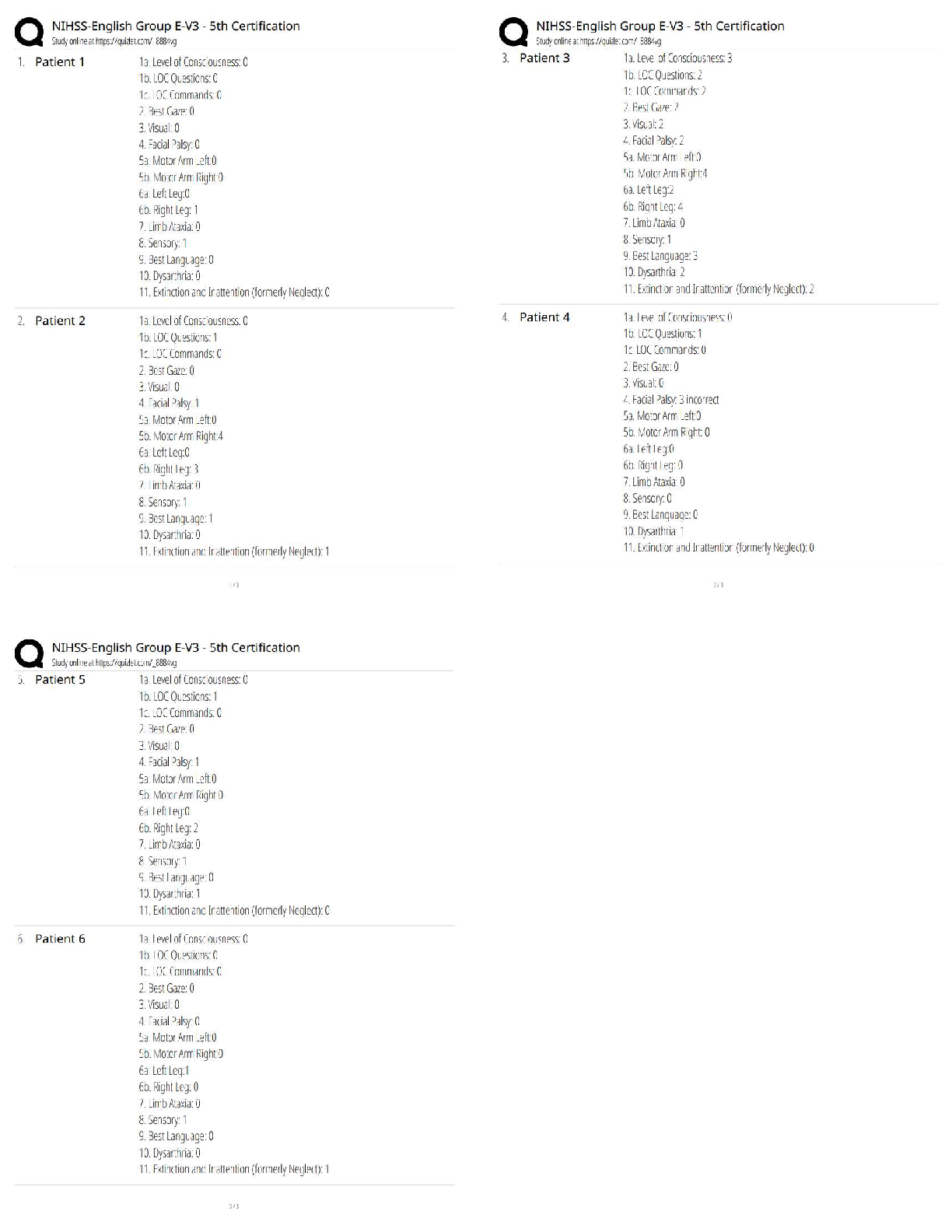
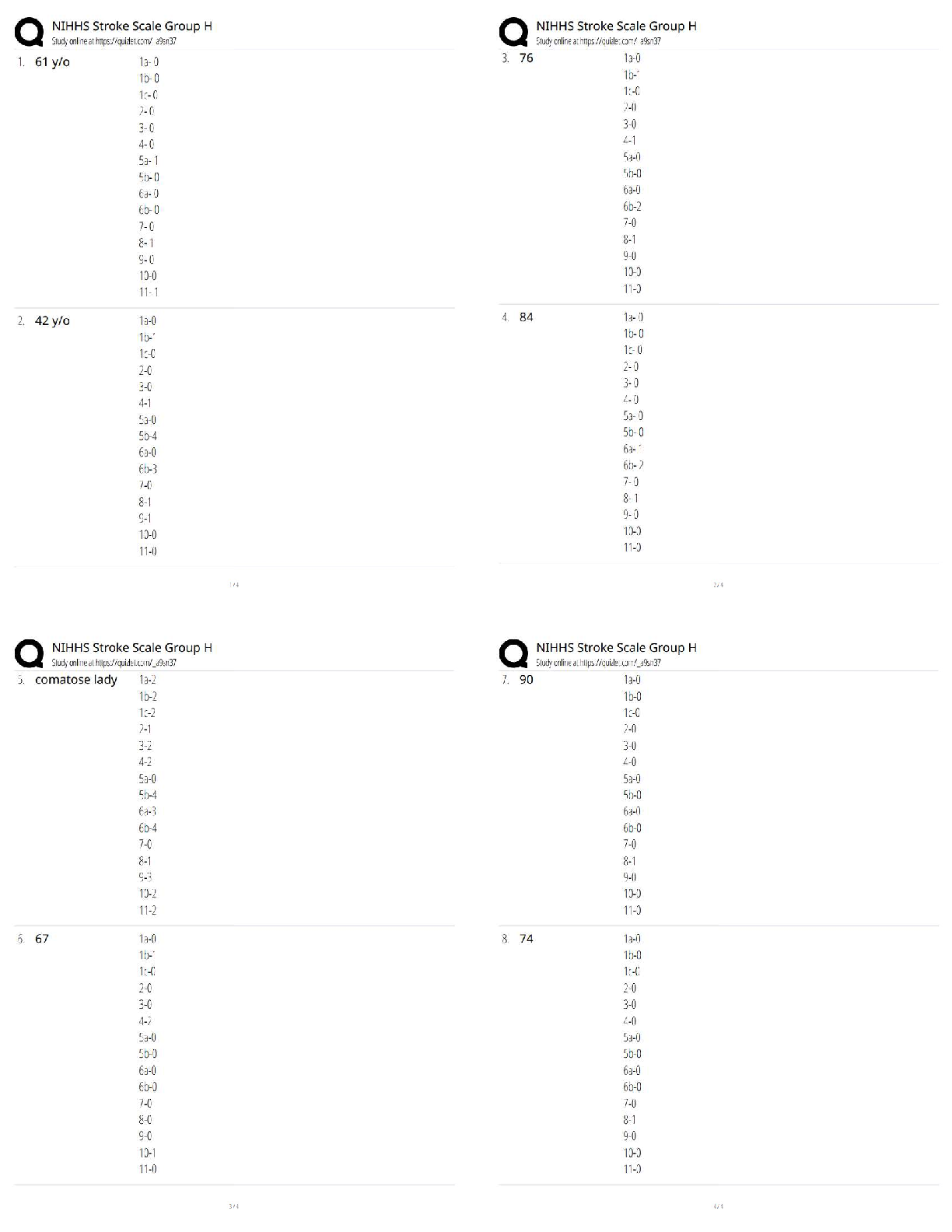
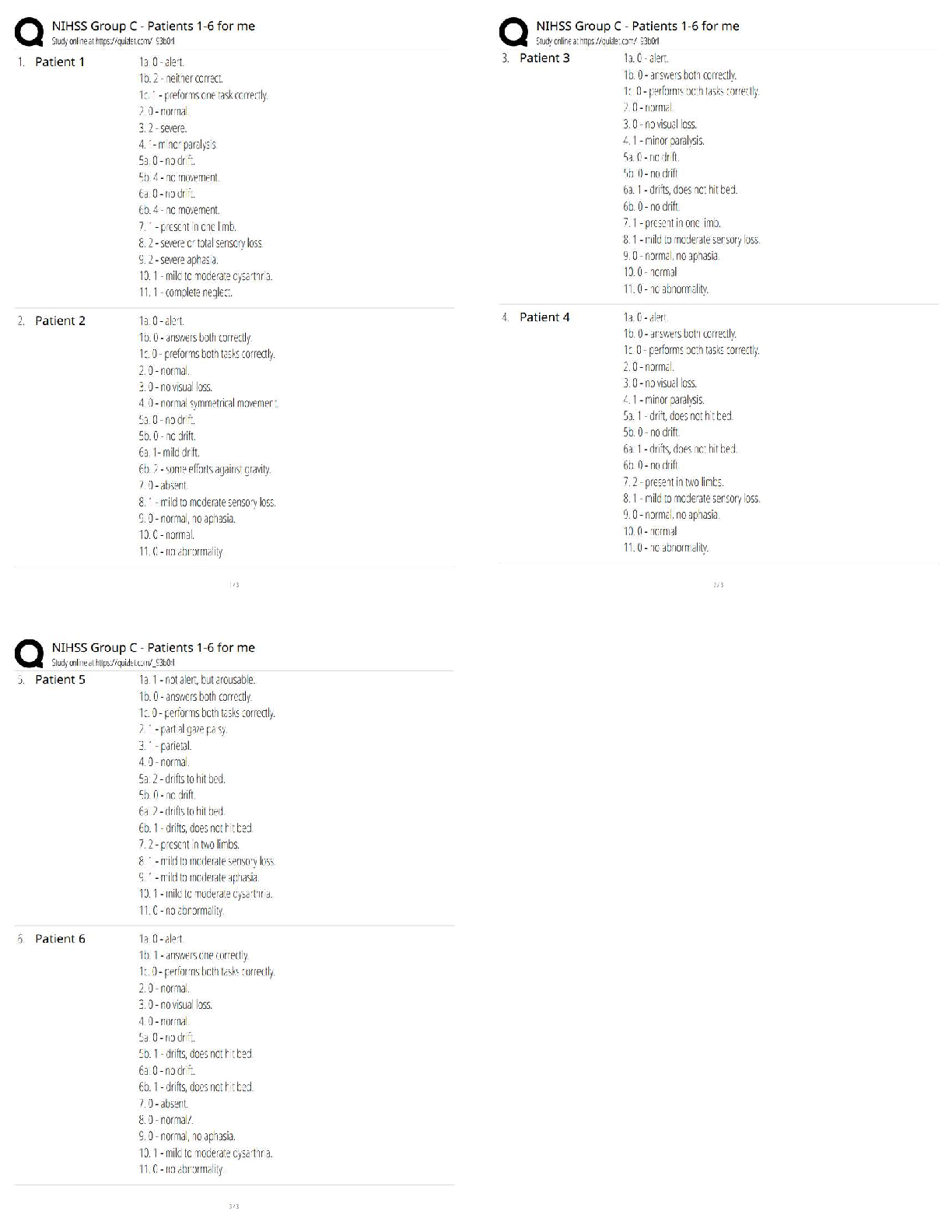
ECE 301 – Digital Electronics Spring 2013 Homework #11 Solutions 1. B/V: problem 8.1 (Sequential Logic Circuit design – Moore machine) A Finite State Machine (FSM) is defined by the state-assi ... gned table given below. Derive a sequential logic circuit that realizes this FSM, using D flip-flops. State-Assigned Table with Flip-flop input columns: Using K-maps to derive expressions for the flip-flop inputs and the sequential circuit output: z = Q1.Q0 (Moore machine) Draw the circuit diagram – including combinational logic and flip-flops. 1 of 10 ECE 301 – Digital Electronics Spring 2013 2. B/V: problem 8.3 (State Graph – Mealy machine) Derive the state graph (or state table) for an FSM (Mealy machine) that has an input w and an output z. The machine has to generate z = 1 when the previous four values of w were 1001 or 1111; otherwise, the machine should generate z = 0. Overlapping input patterns are allowed. State Table: State Graph: 2 of 10 ECE 301 – Digital Electronics Spring 2013 3. B/V: problem 8.5 (State Table – Moore machine) Derive a minimal state table for a single-input and single-output Moore-type FSM that produces an output of 1 if in the input sequence it detects either 110 or 101 patterns. Overlapping sequences should be detected. State Table: State Reduction using Partitioning: P3 = (S0, S1) (S2) (S3) (S4) (S5) P3 contains several groups – each group of “equivalent” states is determined by considering the next states of the states in the groups from partition P2. 3 of 10 ECE 301 – Digital Electronics Spring 2013 P4 = (S0) (S1) (S2) (S3) (S4) (S5) P4 contains groups each containing one state – this implies that each state is unique and is required in the reduced state table. Reduced State Table: 4 of 10 ECE 301 – Digital Electronics Spring 2013 4. B/V: problem 8.6 (State Table – Mealy machine) Repeat the previous problem for a Mealy-type FSM. Reduced State Table: 5 of 10 ECE 301 – Digital Electronics Spring 2013 5. B/V: problem 8.11 (Reduced State Table – Moore machine) TBD. – Digital Electronics Spring 2013 6. B/V: problem 8.12 (Reduced State Table – Moore machine) Derive a minimal state table for an FSM that acts as a three-bit parity generator. For every three bits that are observed on the input w during three consecutive clock cycles, the FSM generates the parity bit p = 1 if and only if the number of 1s in the three-bit sequence is odd. State Table: State Reduction using Partitioning: P3 = (S0, S1, S2, S5) (S3) (S4) P3 contains several groups – each group of “equivalent” states is determined by considering the next states of the states in the groups from partition P2. ECE 301 – Digital Electronics Spring 2013 P4 = (S0, S5) (S1) (S2) (S3) (S4) P4 contains several groups – each group of “equivalent” states is determined by considering the next states of the states in the groups from partition P3; if a state is in a group by itself, then it is a unique state and must be included in the reduced state table P5 = (S0, S5) (S1) (S2) (S3) (S4) P5 = P4 Therefore, this is the final partition, and the state reduction process is complete. From the partition it can be seen that states S0 and S5 are equivalent, and, as such, one can be removed from the initial state table; the remaining states are all unique, and, therefore, are all required in the reduced state table. Reduced State Table: The row corresponding to state S5 has been removed from the initial state table, and all references to state S5 in the “next state” part of the table have been replaced with state S0. 8 of 10 ECE 301 – Digital Electronics Spring 2013 7. B/V: problem 8.15 (Sequential Logic Circuit design – using One-hot encoding) Show a state table for the state-assigned table given below, using A, B, C, and D for the four rows in the table. Construct a new state-assigned table using one-hot encoding. For states A, B, C, and D, use the codes Q3Q2Q1Q0 = 0001, 0010, 0100, and 1000, respectively. Design a sequential circuit using D flip-flops. State-Assigned Table (using Binary Encoding): State Table: State-Assigned Table (using Binary Encoding): 9 of 10 ECE 301 – Digital Electronics Spring 2013 Next-state equations: Characteristic equation for the D flip-flop: Q+ = D Input equations for D flip-flops: Draw the circuit diagram – including combinational logic and flip-flops. 10 of 10 [Show More]

Last updated: 3 years ago

Preview 1 out of 10 pages