Mathematics > QUESTIONS & ANSWERS > University of California, Berkeley - CS 70. DIS4A. Discrete Mathematics and Probability Theory Summ (All)

University of California, Berkeley - CS 70. DIS4A. Discrete Mathematics and Probability Theory Summer 2020 Course Notes. Plus Questions and Answers.

Document Content and Description Below

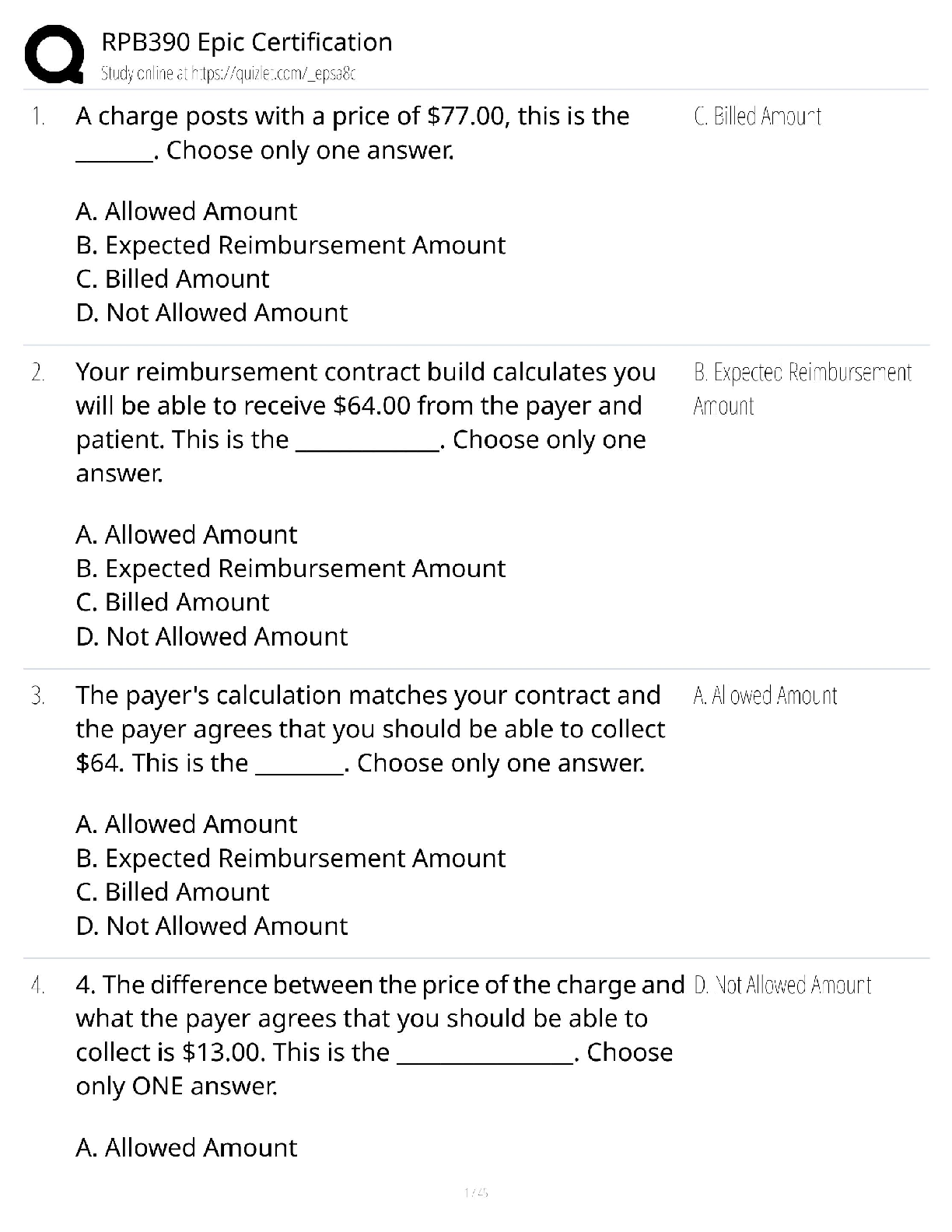
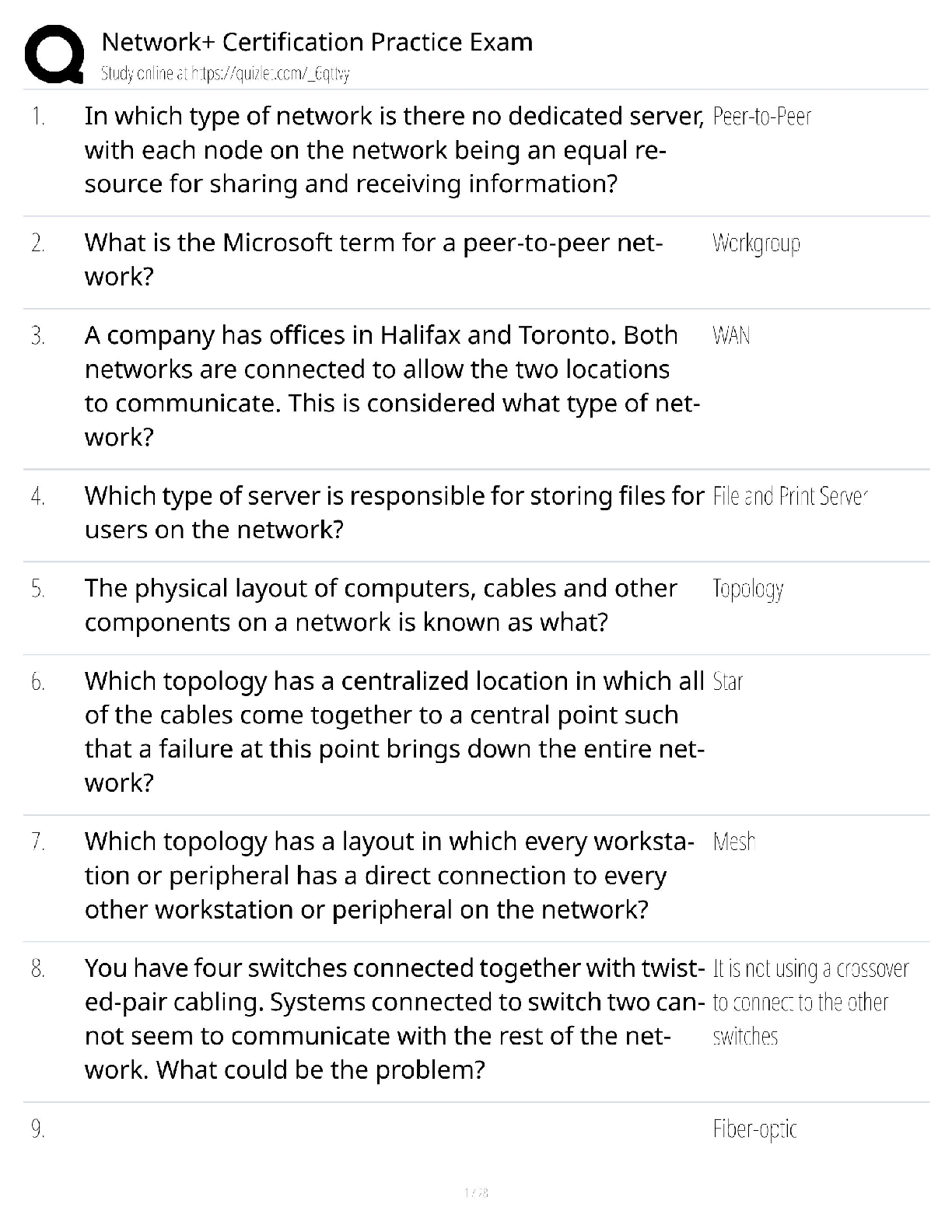
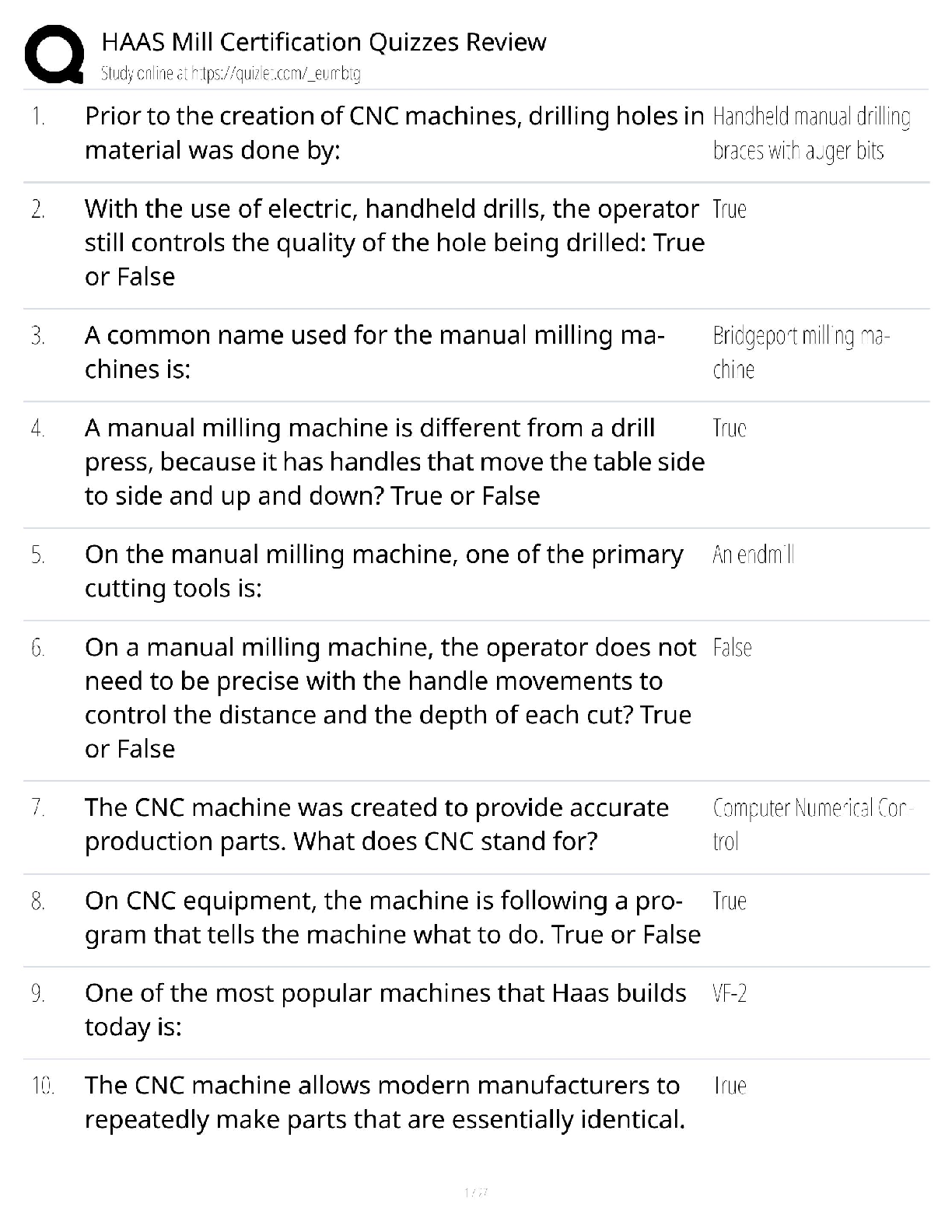
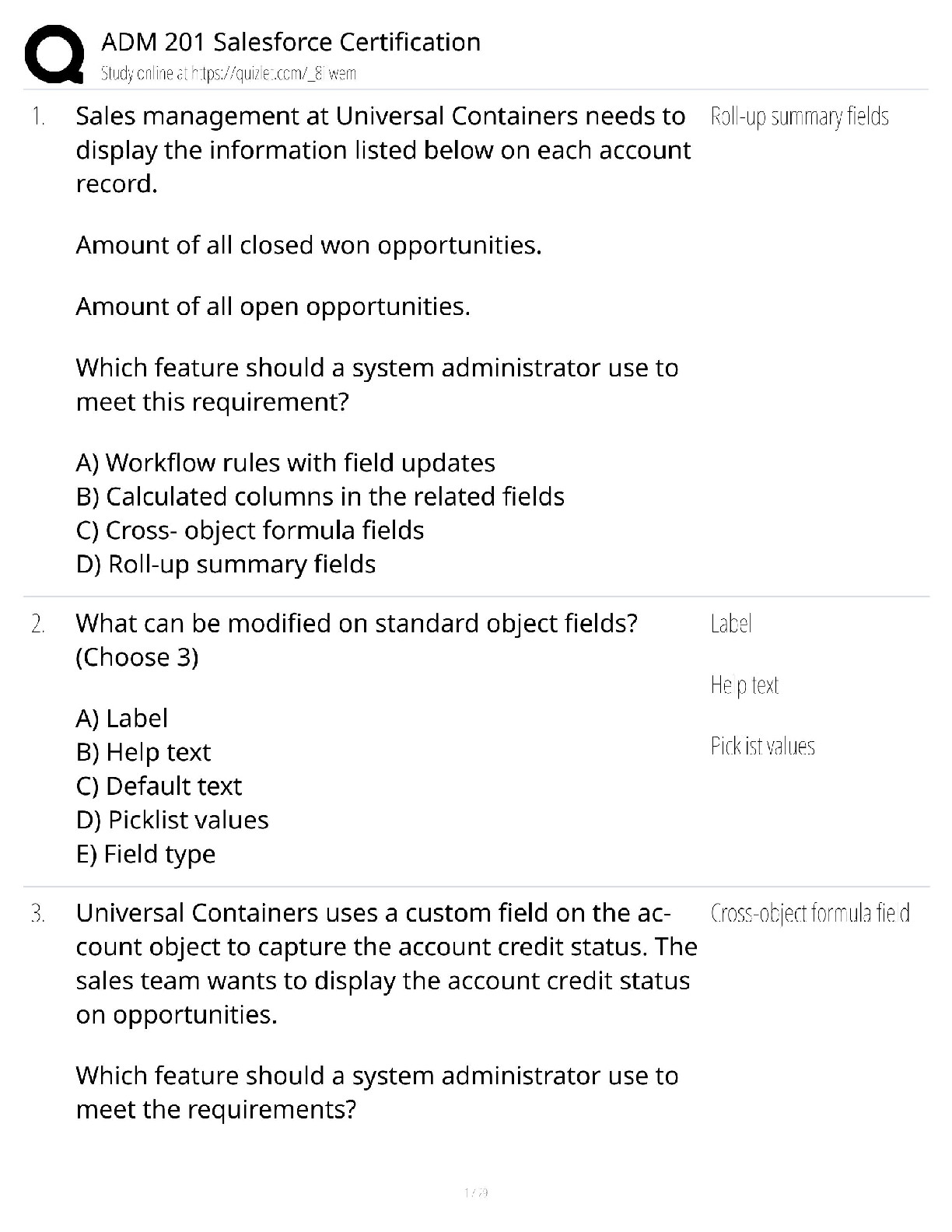
CS 70 Discrete Mathematics and Probability Theory Summer 2020 Course Notes Dis 4A 1 Clothing Argument (a) There are four categories of clothings (shoes, trousers, shirts, hats) and we have ten dist... inct items in each category. How many distinct outfits are there if we wear one item of each category? (b) How many outfits are there if we wanted to wear exactly two categories? (c) How many ways do we have of hanging four of our ten hats in a row on the wall? (Order matters.) (d) We can pack four hats for travels (order doesn’t matter). How many different possibilities for packing four hats are there? Can you express this number in terms of your answer to part (c) Counting on Graphs + Symmetry (a) How many distinct undirected graphs are there with n labeled vertices? Assume that there can be at most one edge between any two vertices, and there are no edges from a vertex to itself. The graphs do not have to be connected. (b) How many distinct cycles are there in a complete graph Kn with n vertices? Assume that cycles cannot have duplicated edges. Two cycles are considered the same if they are rotations or inversions of each other (e.g. (v1;v2;v3;v1), (v2;v3;v1;v2) and (v1;v3;v2;v1) all count as the same cycle). (c) How many ways are there to color a bracelet with n beads using n colors, such that each bead has a different color? Note: two colorings are considered the same if one of them can be obtained by rotating the other. CS 70, Summer 2020, Dis 4A 1 https://www.coursehero.com/file/65280672/dis4A-solpdf/ This study resource was shared via CourseHero.com(d) How many ways are there to color the faces of a cube using exactly 6 colors, such that each face has a different color? Note: two colorings are considered the same if one can be obtained from the other by rotating the cube in any way Maze Let’s assume that Tom is located at the bottom left corner of the 9 × 9 maze below, and Jerry is located at the top right corner. Tom of course wants to get to Jerry by the shortest path How many such shortest paths exist? (b) How many shortest paths pass through the edge labeled X? The edge labeled Y? Both the edges X and Y? Neither edge X nor edge Y? [Show More]

Last updated: 2 years ago

Preview 1 out of 4 pages

Buy Now

Instant download

We Accept: