University of California, Berkeley - CS 70 Midterm-Sol. CS 70 Discrete Mathematics and Probability Theory. Fall 2020 Midterm Solutions.

Document Content and Description Below

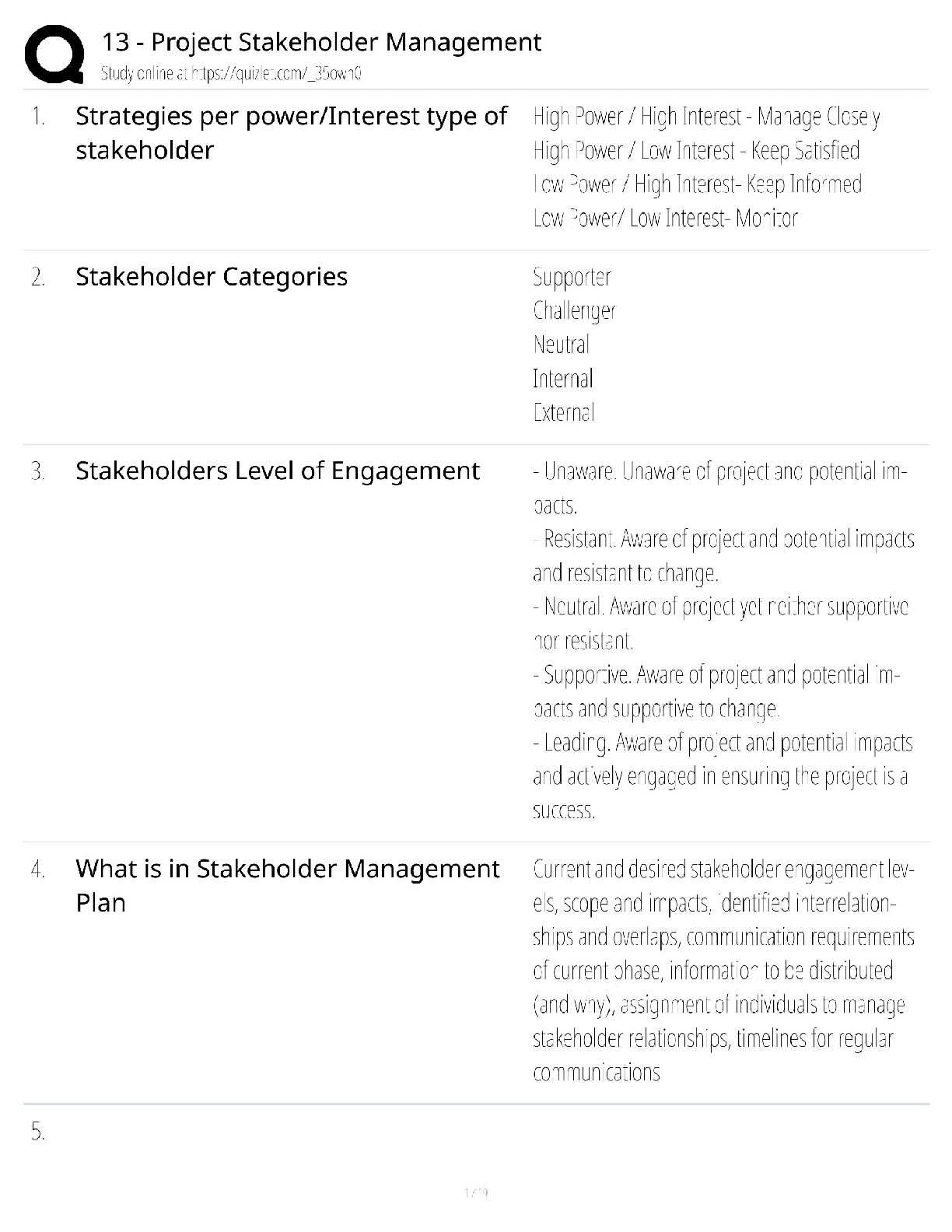
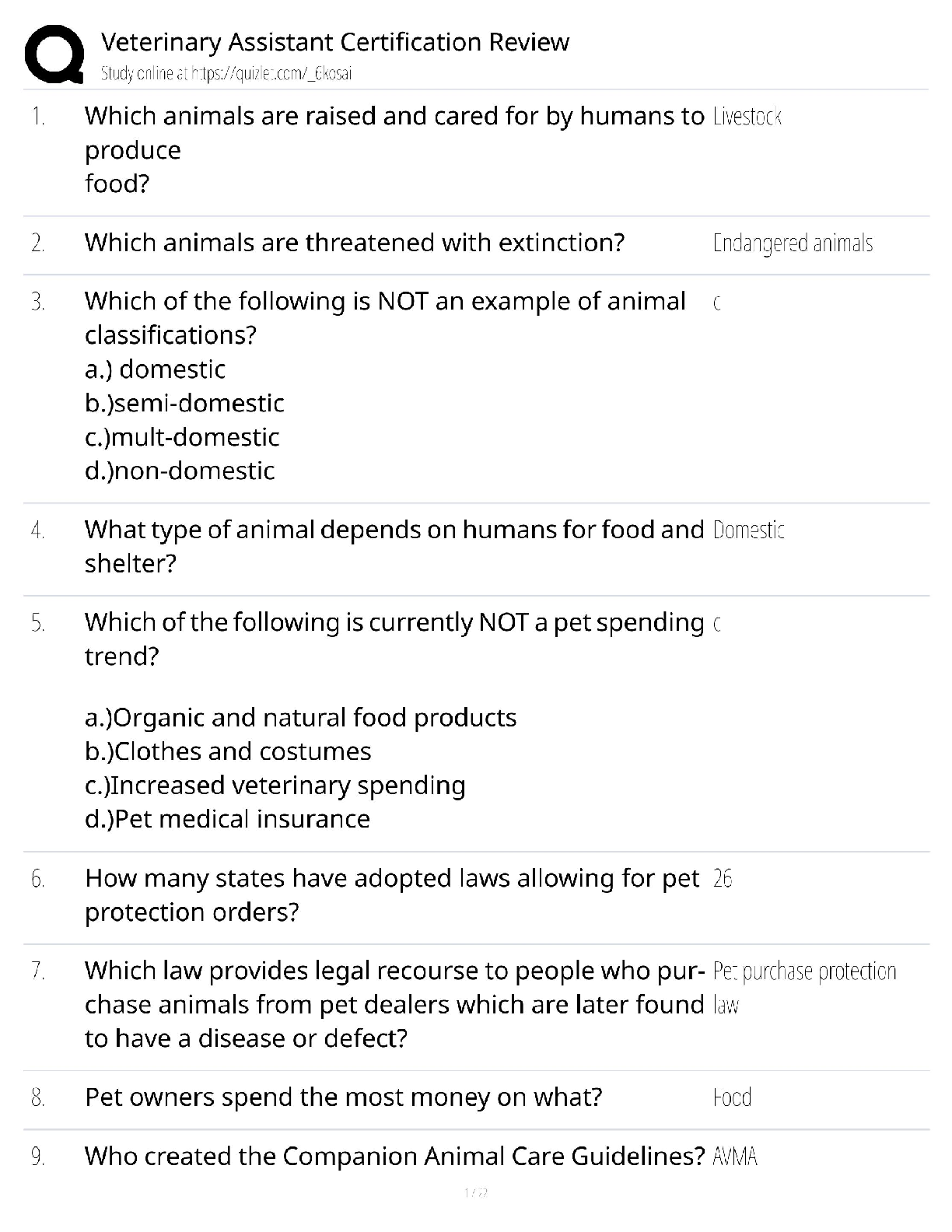
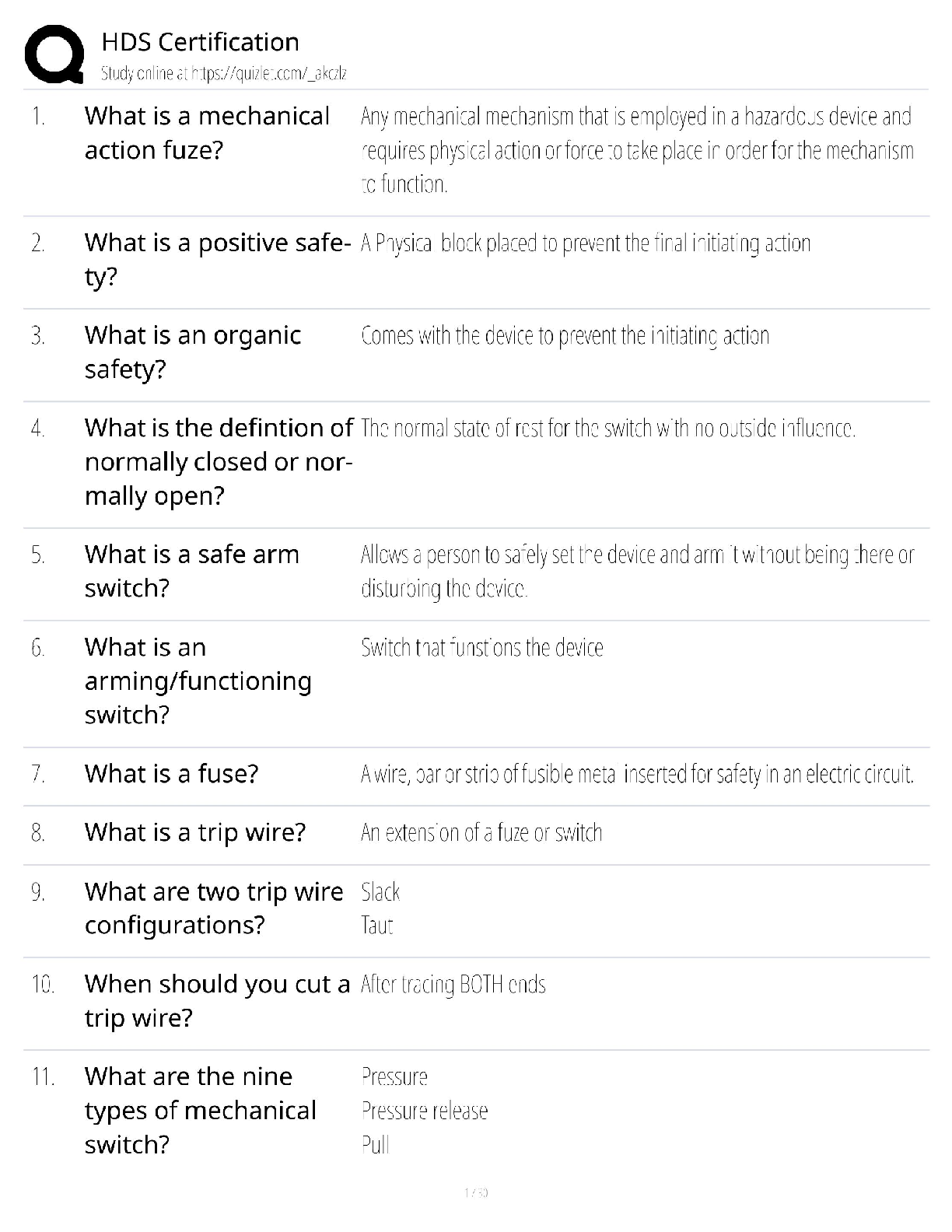
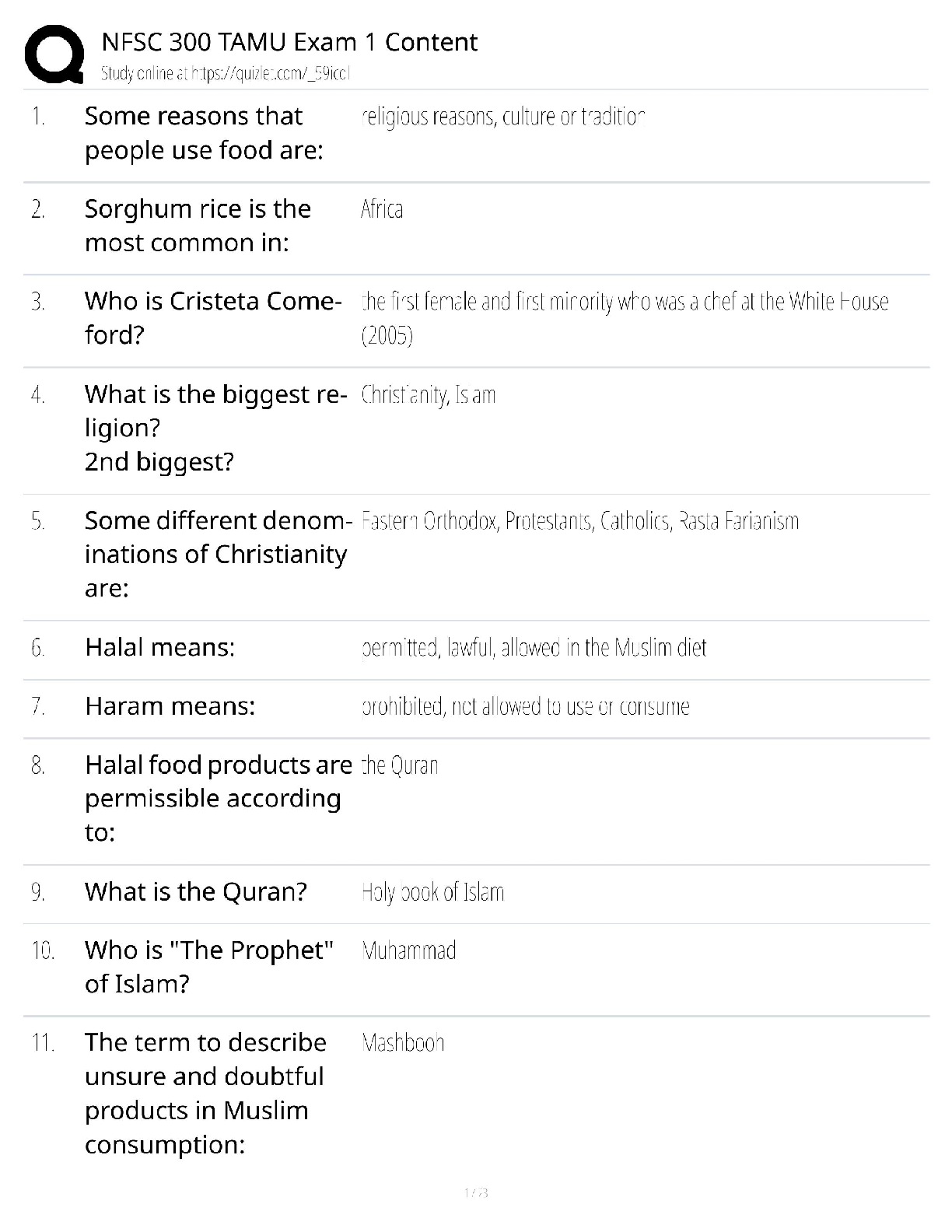
CS 70 Discrete Mathematics and Probability Theory Fall 2020 Rao Midterm Solutions PRINT Your Name: SIGN Your Name: OS K I Do not turn this page until your instructor tells you to do so. CS 70... , Fall 2020, Midterm Solutions 1 SID: 1. Pledge. Berkeley Honor Code: As a member of the UC Berkeley community, I act with honesty, integrity, and respect for others. In particular, I acknowlege that: • I alone am taking this exam. Other than with the instructor and GSI, I will not have any verbal, written, or electronic communication about the exam with anyone else while I am taking the exam or while others are taking the exam. • I will not have any other browsers open while taking the exam. • I will not refer to any books, notes, or online sources of information while taking the exam, other than what the instructor has allowed. • I will not take screenshots, photos, or otherwise make copies of exam questions to share with others. Signed: 2. Warmup, Propositions, Proofs: 2 points/part unless otherwise stated. 1. :(P =) Q) ≡ (P^ :Q) Answer: 2. 8x 2 S;(Q(x) _P(x)) ≡ (8x 2 S;Q(x)) _ (8x 2 S;P(x)) Answer: For the following two parts, assume Q(x;y) and P(x) are predicates over the domain of x;y. 3. (9x;8y;Q(x;y) ^P(x)) =) 9x;P(x) Answer: 4. (9x;8y;Q(x;y) _P(x)) =) 9x;P(x) Answer: 5. P(0) ^ (8n 2 N P(n) =) P(n+1)) =) :(9n 2 N:P(n)) Answer: 6. More Cards to Flip? (4 points.) Your friend states that “All plants that are shipped to a Californian address must have originated in California”. Staying indoors with windows closed all day, you are suddenly intrigued by this rule. Which of the following would you do to test (falsify) your friend’s statement? (a) Find the destination of Megan’s English Ivy plant, being shipped from Oregon (b) Find the destination of Tyler’s Rubber Tree plant, being shipped from California (c) Find the origin of Albert’s Aloe Vera plant, who received it in California (d) Find the origin of Lili’s Bamboo Palm plant, who received it in Seattle (Answer may include more than one.) Answer: 2 SID: 7. If n and m have the same prime factorizations, then they are the same number. Answer: 8. If xy = n and uv = n, with x < y and u < v, then x = u and y = v. Answer: 9. If djx and djx+2y then djy. Answer:. 3. Stable Matchings. 2 points/part. Stable Matching: In the following consider a stable matching instance with n candidates and n jobs each with complete preference lists. 1. The only stable pairing in any instance is produced by the job propose and candidate reject algorithm. Answer: 2. Any job has a unique pessimal candidate. Answer:. 3. If a candidate rejects a job in the job propose and reject algorithm, there is no stable pairing where that candidate and job are paired. Answer: 4. Consider any stable matching instance, and a run of the job propose and candidate reject algorithm, where exactly one candidate, c, misbehaves. In particular, rejects some job j falsely (that is rejects a job j for a job j0 that c prefers less). In this scenario, c is the only candidate that can be in a rogue couple in the final pairing. Answer: 5. There is no stable pairing where every job is paired with its least preferred candidate. Answer: 4. Graphs. 2 points/part unless otherwise indicated. All graphs are simple in this problem, unless otherwise stated. 1. Any tree is bipartite. Answer: 2. Any graph G = (V;E) with jEj ≥ jVj is connected. Answer: 3 SID: 3. Every graph that is vertex-colorable with d colors has max degree d -1. Answer: 4. Any cycle can be edge colored with 2 colors. (Recall edge coloring is a coloring of edges so that any pair of edges incident to the same vertex have different colors.) Answer: 5. (4 points) For a graph G, consider a walk which contains any edge at most once and contains all the edges incident to each of its two distinct endpoints, u and v. Recall that a walk is a sequence of edges where successive edges share an endpoint, thus this walk does not reuse edges but does use all the edges incident to u and v. If the endpoints, u and v, are different: (A) Their degrees must be the same. (B) Each must have even degree. (C) Each must have odd degree. (D) The sum of the degrees of the two vertices is even. Answer all that are true. Answer: 6. Any graph with v vertices and v-k edges for k ≥ 0 and has exactly one cycle has connected components. Answer: 7. There is a simple graph with average degree of exactly 2 that has no cycles. (Recall that simple means there is at most one edge between any pair of nodes.) Answer: 8. There is a directed graph, where the sum of the outdegrees over all vertices is greater than the sum of indegrees over all vertices. Answer: 5. Planar graphs. 3 points/part. Consider a connected planar graph with v ≥ 3 vertices, and where every cycle has length at least 6. 1. Give an upper bound on the number of edges, e in terms of the number of vertices, v. (Recall, for example, that any for any planar graph e ≤ 3v-6. Your upper bound should be as tight as possible.) Answer: 2. How many colors is always sufficient to vertex colored such a graph? Answer: 3 4 SID: 6. Modular Arithmetic:short answer. 2 points per part. 1. What is 211 (mod 11)? Answer 2. What is 225 (mod 33)? Answer: 3. ab ≡ 0 (mod N) implies that a ≡ 0 (mod N) or b ≡ 0 (mod N). Answer: 4. For primes p and q, find all values of x 2 f1;:::; pq-1g, where xj(ak(p-1)(q-1)+1 -a)? Answer: 5. If a 6= 1 (mod N) and ak(N-1) 6= 1 (mod N) then N is not prime. Answer: 6. How many solutions are there to ax = b (mod n), if gcd(a;n) = d and gcd(b;n) = d? Answer: 7. Find x 2 f0;:::; pq-1g where x = a (mod p) and x = 0 (mod q) where p and q are prime? (Answer expression that may involve a, p, q, (mod q), (mod p) and inverses, e.g., (q-1 (mod p)).) Answer: 8. For x;y 2 Z for x 6= y, what is the minimum value of jx - yj if x = y = a (mod p) and x = y = b (mod q) for primes p and q? Answer: 7. Another Proof. 3 points/part. Another proof for RSA can be done as follows. 1. Let S be the set of numbers f0;:::; pq - 1g relatively prime to pq. What is jSj? (Recall, a and b are relatively prime if gcd(a;b) = 1.) Answer: 2. For a with gcd(a; pq) = 1, and T = fax (mod pq)jx 2 Sg, what is the size of T? Answer: 5 SID: 3. What is ajTj (mod pq)? Answer: 8. Polynomials: Background. 2 points/part. When we count roots, we mean with multiplicity unless otherwise stated. That is, Q(x) = (x - 2)2 has two roots. Polynomials are over a field unless otherwise specified. 1. If two polynomials of degree 7 in share points then they must be the same (working (mod 17).) (Answer is the smallest integer that makes the statement true.) Answer: 8. 2. If a non-zero polynomial has d roots it must have at least degree . Answer:. 3. How many roots does the polynomial, x2 -2 (mod 5) have? Answer: 4. If a polynomial has d roots it’s degree is at most d. Answer: 5. Given a polynomial Q(x) = P(x)(x-2)(x-4), and d is the degree of Q(x), what is the degree of P(x)? Answer: 6. Given a polynomial Q(x) = P(x)(x-2)(x-4), and if P(x) has r roots, what is the number of roots for Q(x)? Answer: 9. Polynomials: applications. 2 points/part. Recall for secret sharing and error tolerance to erasures and corruptions that one works over arithmetic modulo a prime p. In each of the following situations, how big should p be? (That is, fill in the blank for p ≥ .) 1. One wishes to share a secret with b-bits among n people where any k can reconstruct the secret. Answer: 2. One wishes to communicate a message of n packets with b bits each and wants to tolerate k erasures? Answer: 3. One wishes to communicate a message of n packets with b bits each and wants to tolerate k corruptions? Answer: 10. Counting: Basics. 2 points/part. Let S = f1;:::;ng. 6 SID: (A) All subsets of S. (B) The number of subsets of S of size k. (C) The number of subsets of S of size n-k. (D) The number of ways for k non-negative integers that add up to n. (E) The number of ways for k positive integers that add up do n. For each of the expressions, indicate the letter of the option above that it coresponds to. Provide all answers that match. 1. nk Answer: 2. n-n k. Answer 3. nk--11. Answer: Answer: 5. 2n Answer: 11. Counting and Polynomials. 2 points/part. Counting and Polynomials. Assume all polynomials are over (mod p) where p is a prime and p > d. Again, when we count roots, we mean with multiplicity unless otherwise stated. That is, Q(x) = (x-2)2 has two roots. 1. What is the number of roots of a degree 1 polynomial (mod p)? (A degree one polynomial is ax+b, where a is non-zero.) Answer: 2. What is the number of degree d polynomials? Answer: 3. What is the number of exactly degree d polynomials with d distinct roots? Answer: 4. What is the number of exactly degree d polynomials with d roots (allowing for multiplicity)? Answer: 7 SID: . The Remainder of the Exam is written, and you should be scanning 7 pages for you answers. 12. Quick(ish) Proofs. 3pts/3pts/5pts. You must write your answer for each subproblem on a separate clearly labelled page. 1. Prove: If djx and djy+kx then djy for any integer k. Answer: 2. Prove: If n2 -6n+5 is even, then n is odd. Answer: 3. Prove by induction: For all positive natural numbers n ≥ 1 and that 3(7n)+2(5n-3) is divisible by 25. (It may be useful to see that 25 = 32 = 25+7 and that 2a+b = 2a2b:) Answer: 8 SID: 13. Set Operations. 5 points. For a function g, define the image of a set X to be the set g(X) = fy j y = g(x) for some x 2 Xg. Hint: For sets X and Y , X = Y if and only if X ⊆ Y and Y ⊆ X. To prove that X ⊆ Y , it is sufficient to show that (8x) ((x 2 X) =) (x 2 Y)). Let XDY = (X -Y) [ (Y - X), where X -Y = fxjx 2 Xandx 62 Y g. Prove g(X)Dg(Y) ⊂ g(XDY) Answer: 14. Edge Coloring when there is no Hotel California. 4 pts/4pts/5pts. Please write your answer for each part on a separate page for scanning. 1. Show that an even length cycle can be edge colored with 2 colors. (Recall edge coloring is a coloring of edges so that any pair of edges incident to the same vertex have different colors.) Answer: Recall that a bipartite graph G = (U [V;E) where E ⊂ U ×V , i.e., there are two sets U and V and every edge consists of a vertex from U and a vertex from V . It is useful to recall (without proof) that any cycle in a bipartite graph has even length. For the following two parts, we consider a bipartite graph, G = (U [V;E) where every vertex has degree d = 2k. 2. Show that jUj = jV j. Answer: 3. Show that the graph can be edge colored with d = 2k colors. (Hint: a previous part has something to do with k = 1.) Answer: [Show More]

Last updated: 2 years ago

Preview 1 out of 10 pages