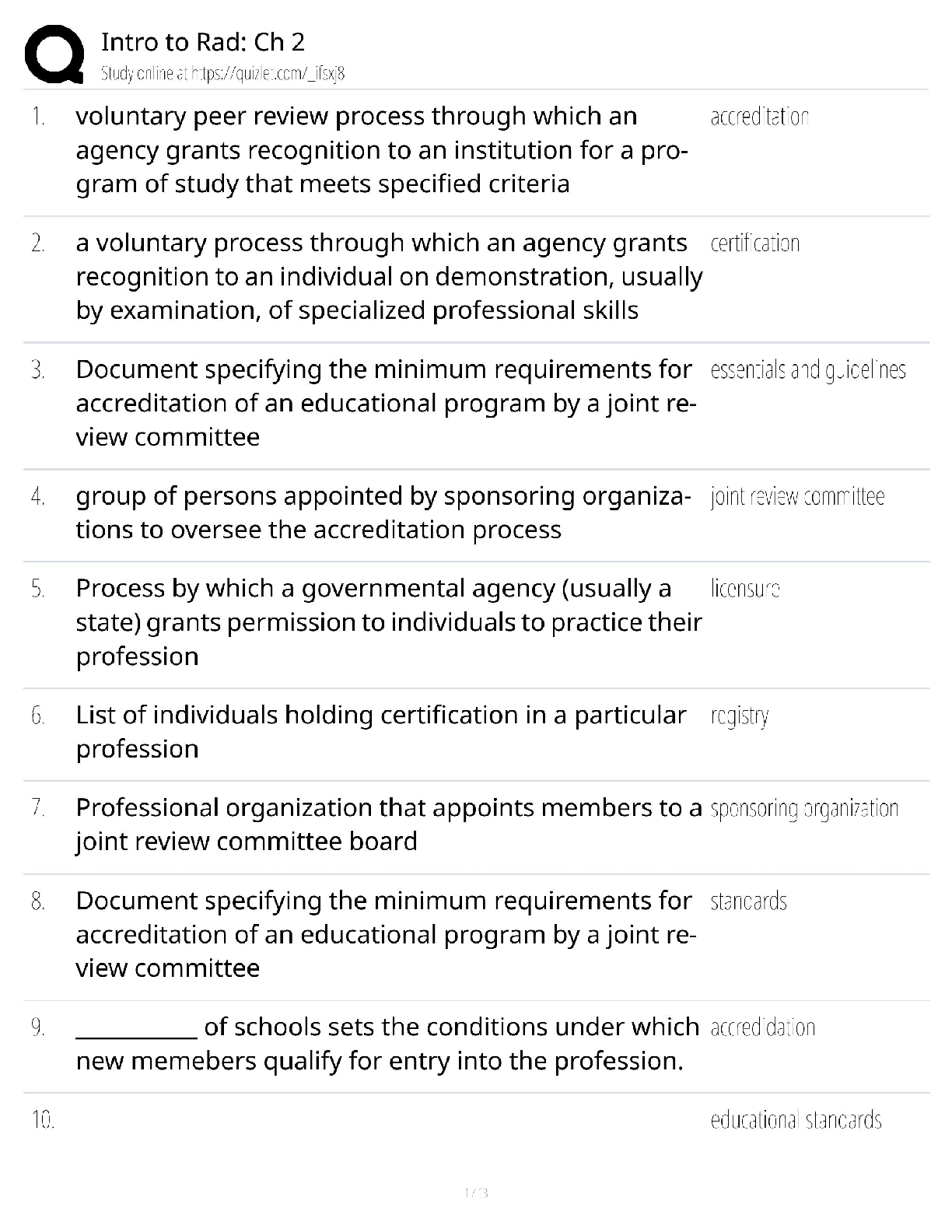
Mathematics > QUESTIONS & ANSWERS > Practice_midterm_2_solutions Harvard University - MATH 2413 ALL ANSWERS CORRECT (All)

Practice_midterm_2_solutions Harvard University - MATH 2413 ALL ANSWERS CORRECT

Document Content and Description Below

Practice midterm 2 - Accelerated multivariable calculus - Solutions 1. Let f(x; y) = (x2 + y2)e−y2. a) Find all critical points of f. Solution: Compute the partial derivatives fx (x; y) = 2xe� ... �y2; fy (x; y) = 2ye−y2 − 2y(x2 + y2)e−y2 = 2y(1 − x2 − y2)e−y2: Solve the system of equations fx(x; y) = 0, fy(x; y) = 0. We obtain x = 0 and y(1 − y2) = 0. It means that the critical points are (0; 0), (0; −1) and (0; 1). b) Classify the critical points of part (a). That is, determine whether they correspond to saddle points, local maximum values or local minimum values of f. Solution: Compute the second order partial derivatives: fxx(x; y) = 2e−y2; fxy(x; y) = −4xye−y2; fyy(x; y) = (4x2y2 − 10y2 + 4y4 − 22 + 2)e−y2: Use the second derivative test. For this compute the determinant D(x; y) = fxxfyy − fxy 2 . For the critical point (0; 0) we have: D(0; 0) = 4 > 0. Since fxx(0; 0) = 2 > 0, the point (0; 0) is a local minimum. For the critical points (0; ±1) we have: D(0; ±1) = −8e−2 < 0. Hence, (0; ±1) are saddle points. [Show More]

Last updated: 3 years ago

Preview 1 out of 6 pages

Buy Now

Instant download

We Accept: