Northeastern University - EECE 56262019FA-EECE5626_HW1_Solutions Image Processing & Pattern Recognition FALL-2019 ( 100 % COMPLETE AND CORRECT SOLUTIONS )

Document Content and Description Below

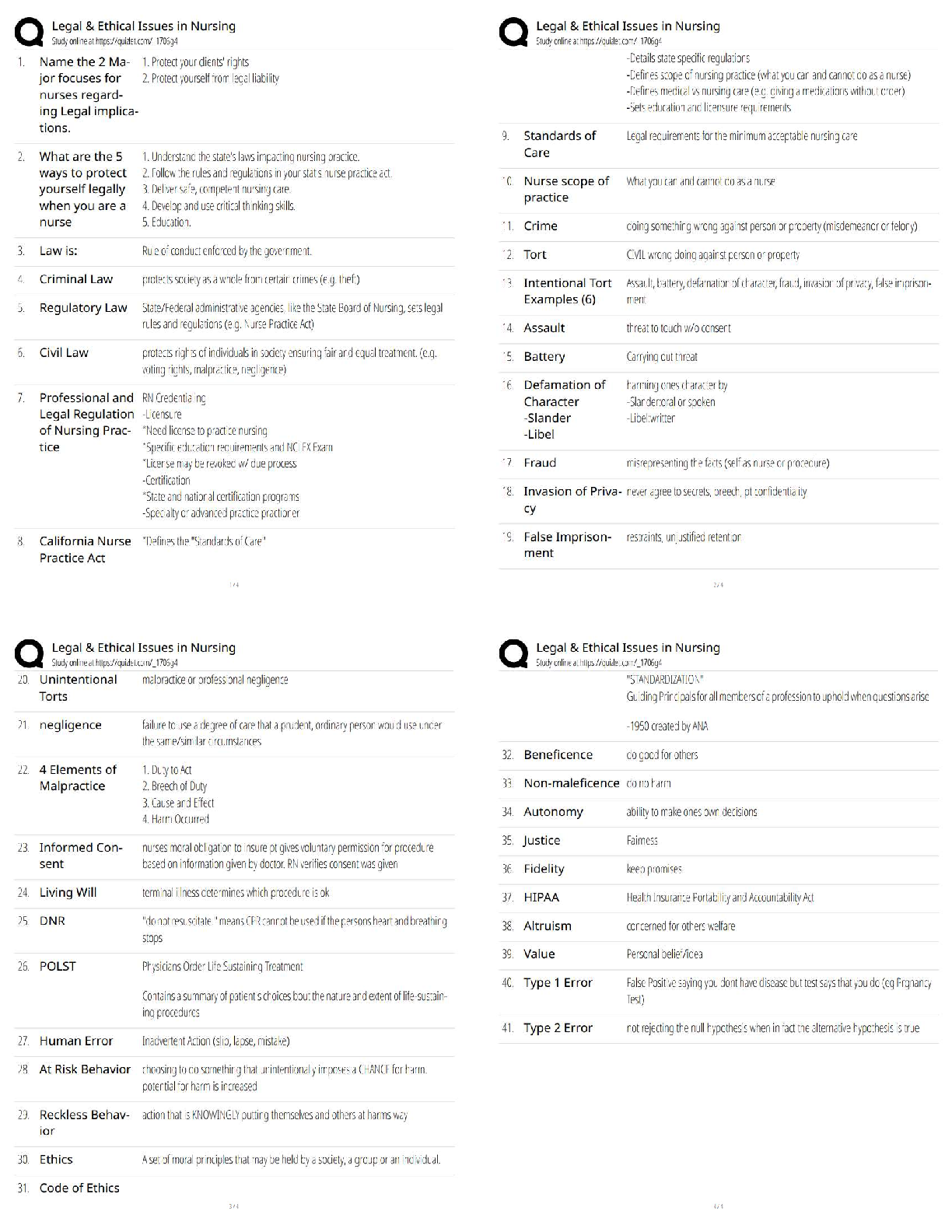
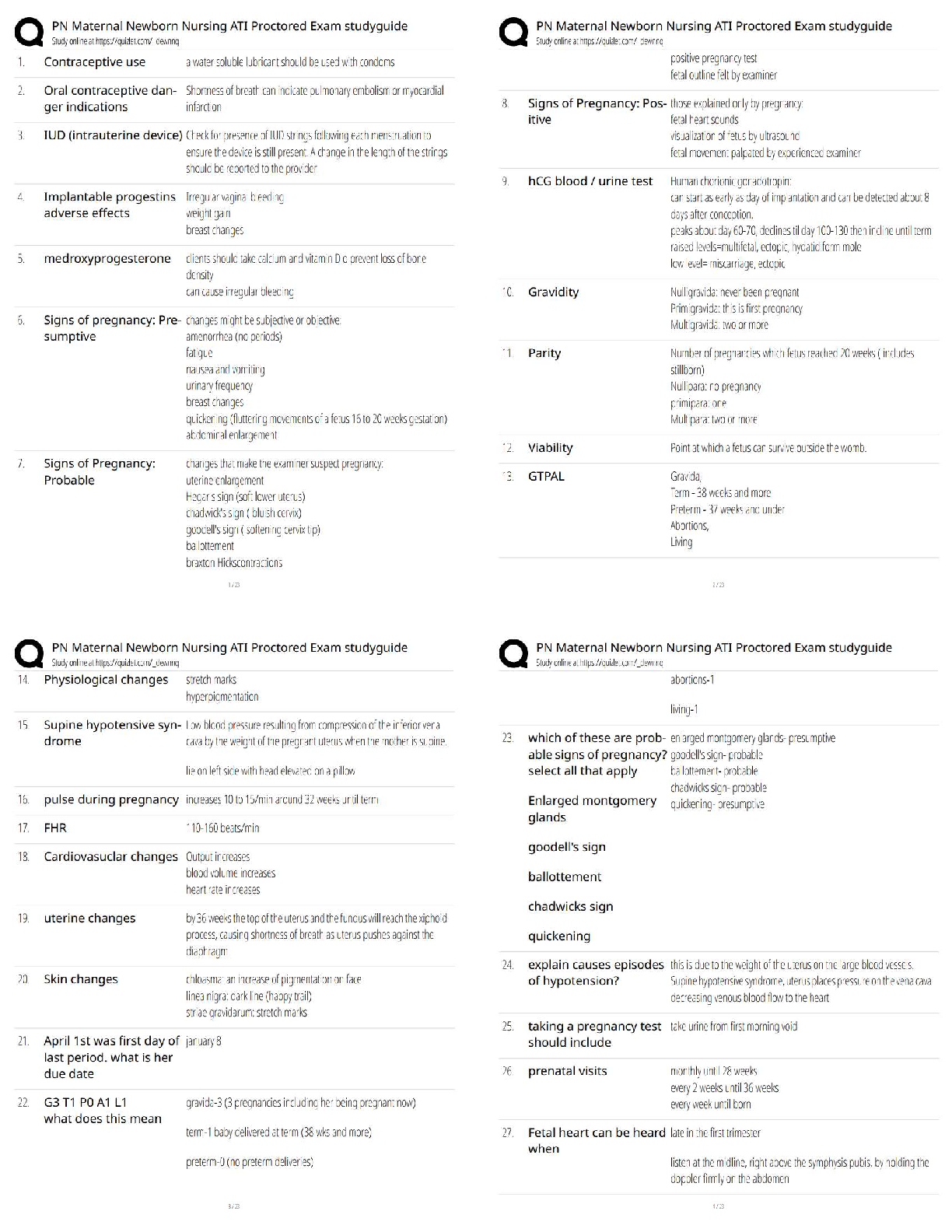
EECE-5626 Image Processing & Pattern Recognition FALL-2019 Homework-1 Solutions P1.1 Text Problem 2.8 (Page 123) A CCD camera chip of dimensions 7£7 mm and 1024£1024 sensing elements, is focused ... on a square, flat area, located 0.5 m away. The camera is equipped with a 35-mm lens. How many line pairs per mm will this camera be able to resolve? (Hint: Model the imaging process as in Fig. 2.3, with the focal length of the camera lens substituting for the focal length of the eye.) Solution: From the geometry of Fig. 2.3 in the textbook, 7 mm/35 mm ˘ z/500 mm, or z ˘ 100 mm. So the target size is 100 mm on the side. We have a total of 1024 elements per line, so the resolution of 1 line is 1024/100 ˘ 10 elements/mm. For line pairs we divide by 2, giving an answer of 5 lp/mm. P1.2 Text Problem 2.10 (Page 124). An automobile manufacturer is automating the placement of certain components on the bumpers of a limited-edition line of sports cars. The components are color-coordinated, so the assembly robots need to know the color of each car in order to select the appropriate bumper component. Models come in only four colors: blue, green, red, and white. You are hired to propose a solution based on imaging. How would you solve the problem of determining the color of each car, keeping in mind that cost is the most important consideration in your choice of components? Solution: One possible solution is to equip a monochrome camera with a mechanical device that sequentially places a red, a green, and a blue pass filter in front of the lens. The strongest camera response determines the color. If all three responses are approximately equal, the object is white. A faster system would utilize three different cameras, each equipped with an individual filter. The analysis then would be based on polling the response of each camera. This system would be a little more expensive, but it would be faster and more reliable. Yet another alternative would be to use a color camera directly, and then use software algorithms to determine the color being seen by the camera. In order to determine if this solution is cheaper than the the 3-camera approach we would have to know the cost of the hardware and software needed to implement the detection algorithm. Note that all solutions assume that the field of view of the camera(s) is such that it is completely filled-in by a uniform color [i.e., the camera(s) is (are) focused on a part of the vehicle where only its color is seen. Otherwise further analysis would be required to isolate the region of uniform color, which is all that is of interest in solving this problem. Illumination should be such that there are no reflections, so that all images are uniform to make color detection easier and faster (and less expensive).2 FALL-2019: HOMEWORK-1 SOLUTIONS : EECE-5626 P1.3 Text Problem 2.16 parts (b) and (c) (Page 124). Consider the two image subsets, S1 and S2 in Figure 1(a): (a) (b) Figure 1: Image subsets in Problem P1.3 With reference to Section 2.5, and assuming that V ˘ {1}, determine whether these two subsets are: (a) 4-adjacent. Solution: Let p and q be as shown in Figure 1(b). Then, S1 and S2 are not 4-connected because q is not in the set N4(p). (b) 8-adjacent. Solution: Subsets S1 and S2 are 8-connected because q is in the set N8(p). (c) m-adjacent. Solution: Subsets S1 and S2 are m-connected because (i) q is in ND(p), and (ii) the set N4(p)\ N4(q) is empty. P1.4 Text Problem 2.20 (Page 125). Consider the image segment shown in the following figure: 3 1 2 1 (q) 2 2 0 2 1 2 1 1 (p) 1 0 1 2 (a) As in Section 2.5, let V ˘ {0,1} be the set of intensity values used to define adjacency. Compute the lengths of the shortest 4-, 8-, and m-path between p and q in the following image. If a particular path does not exist between these two points, explain why. Solution: When V ˘ {0,1} a 4-path does not exist between p and q because it is impossible to get from p to q by traveling along points that arc both 4-adjacent and also have values from V . Figure 2(a) shows this condition; it is not possible to get to q. The shortest 8-path is shown in Figure 2(b); its length is 4. The length of the shortest m-path (shown in magenta) is 5. Both of these shortest paths are unique in this case. (b) Repeat (a) but using V ˘ {1,2}. Solution: One possibility for the shortest 4-path when V ˘ {1,2} is shown in Figure 2(c); its length is 6. It is easily verified that another 4-path of the same length exists between p and q. One possibility for the shortest 8-path (it is not unique) is shown in Figure 2(d); its length is 4. The length of a shortest m-path (shown in magenta) is 6. This path is not unique. [Show More]

Last updated: 2 years ago

Preview 1 out of 13 pages