Stanford UniversityCS 103410 Problem Set 8.

Document Content and Description Below

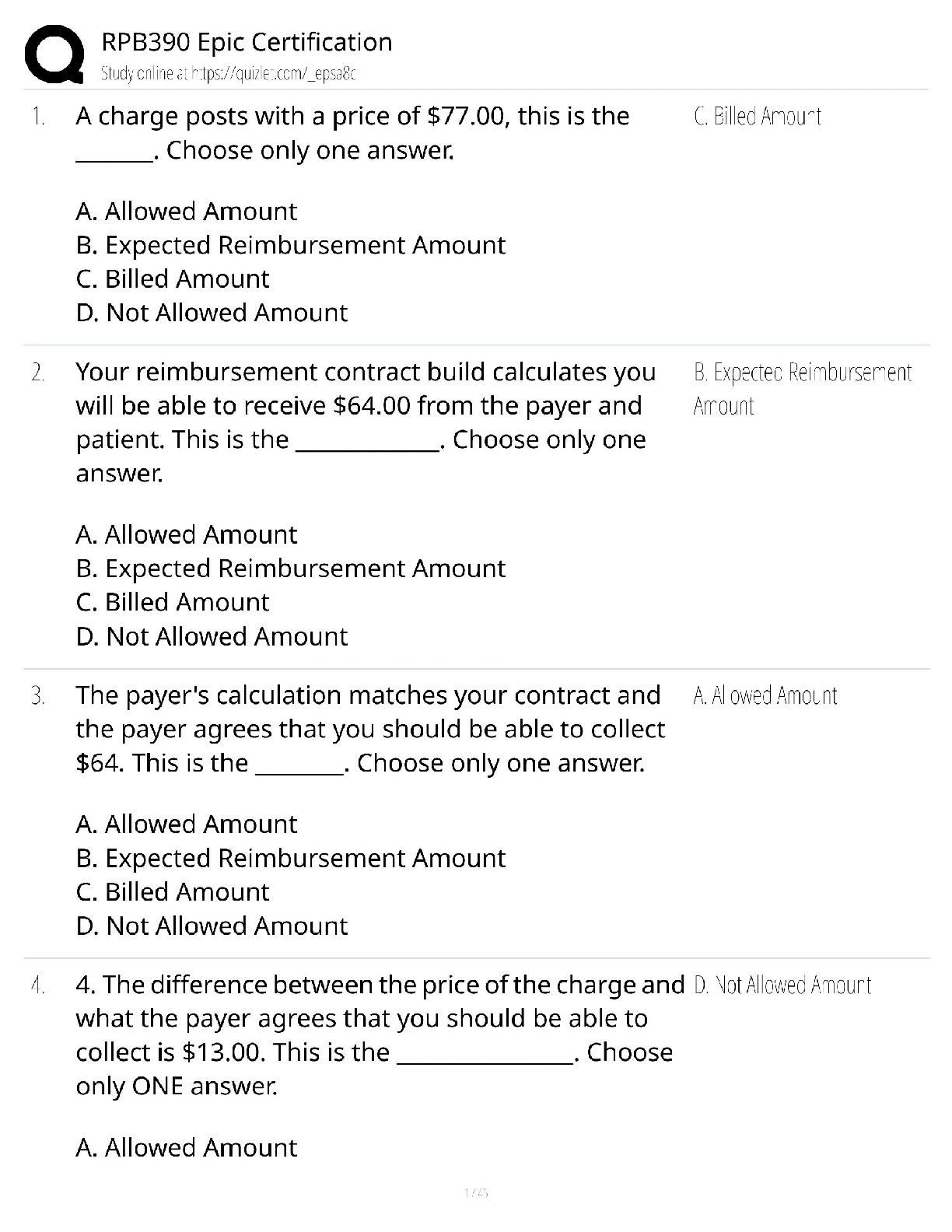
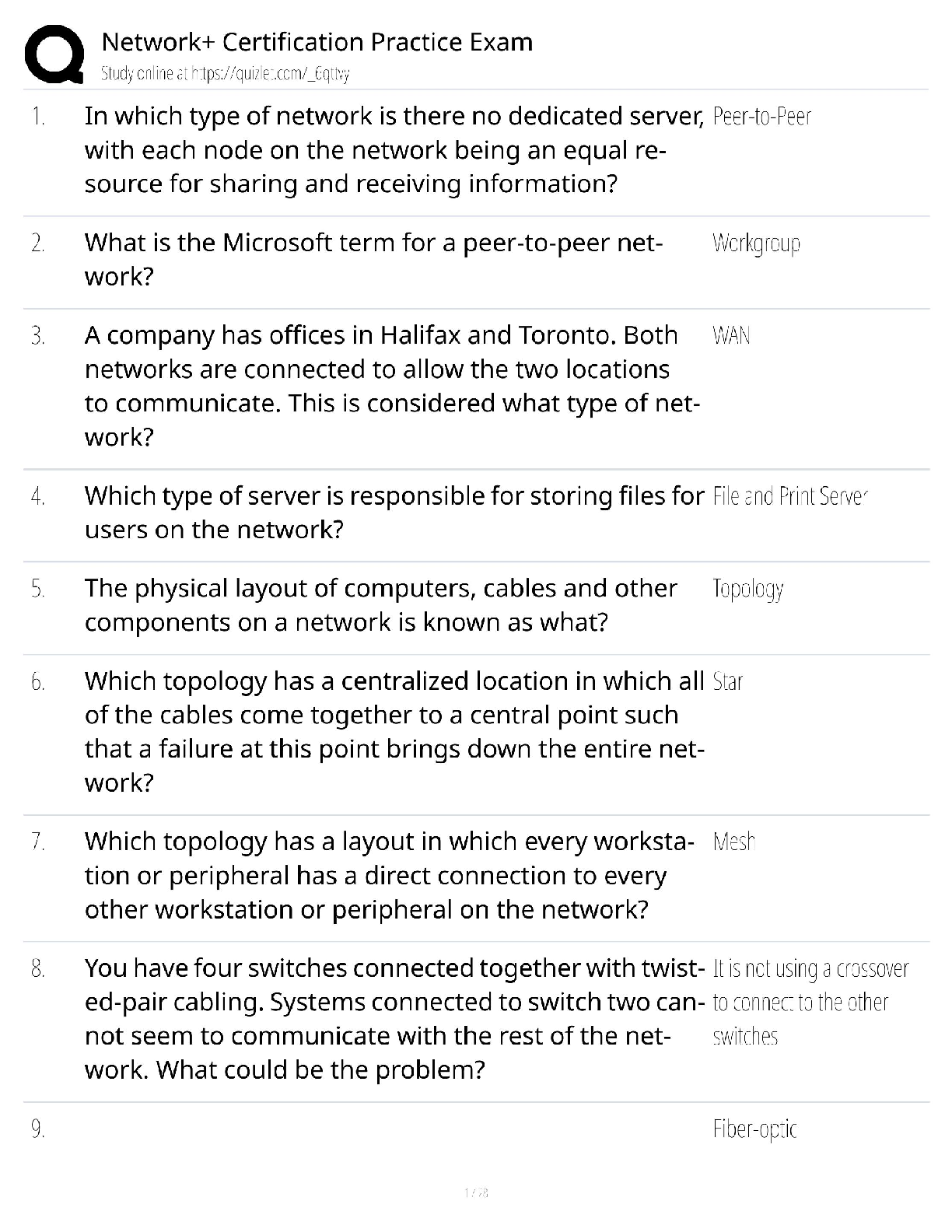
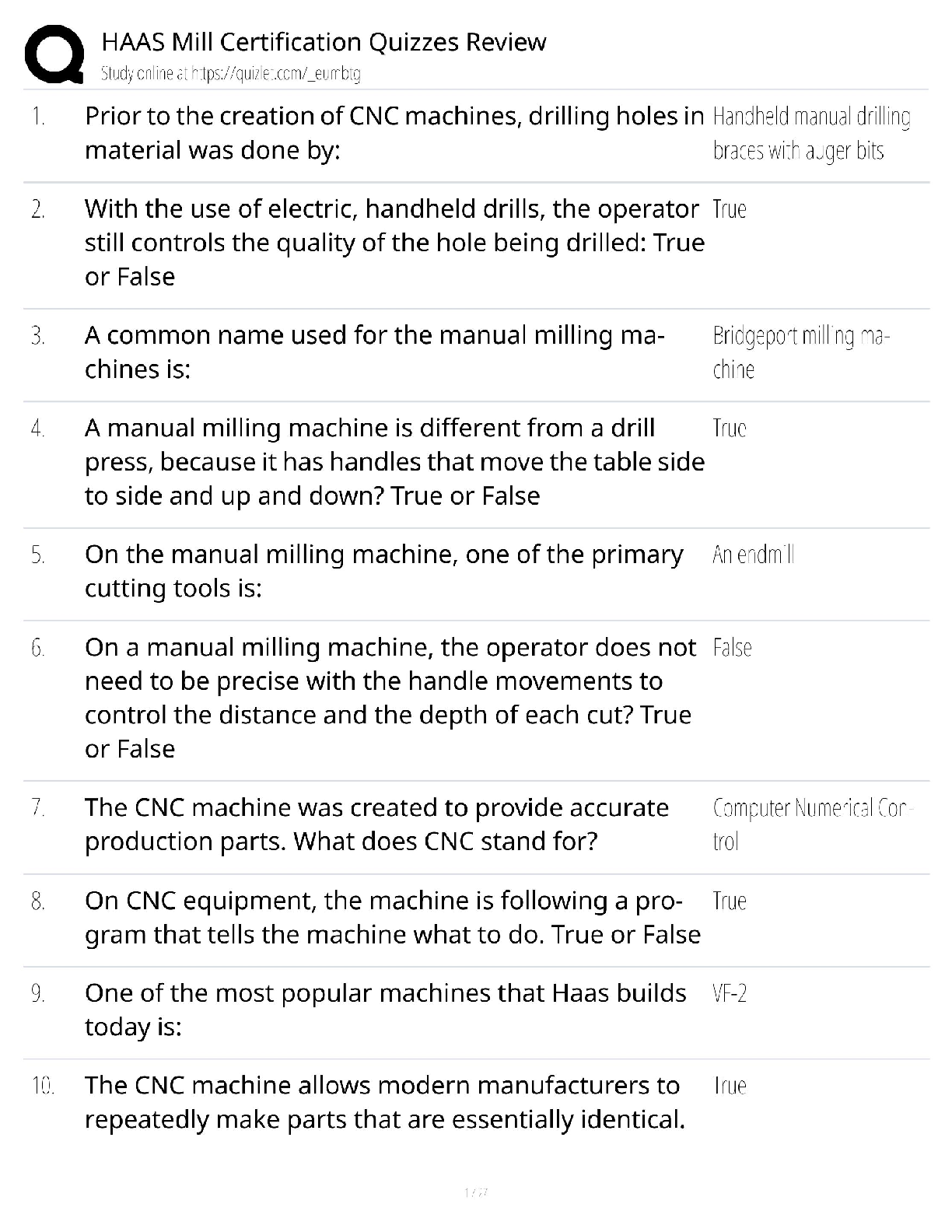
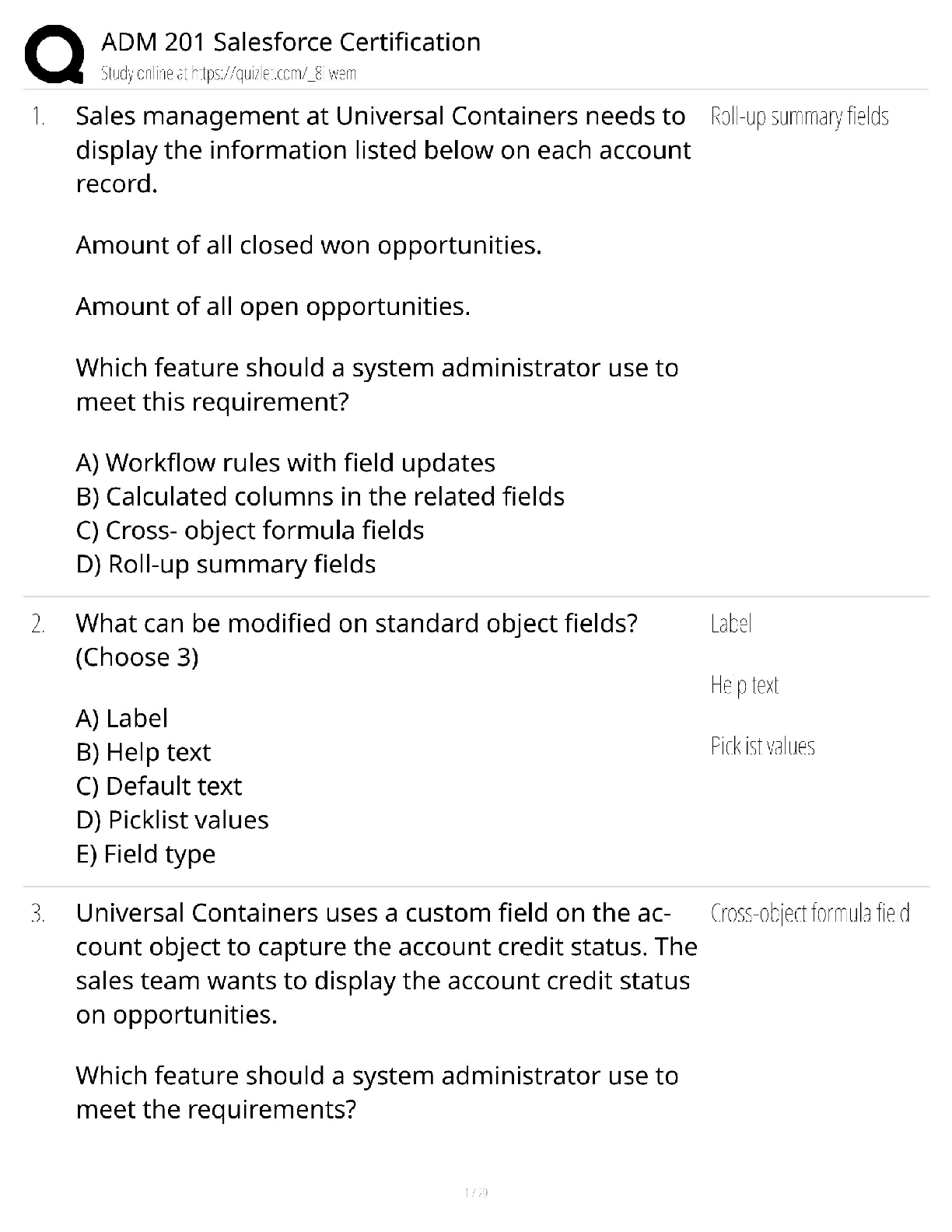
CS103 Handout 41 Spring 2018 Problem Set 8 In this problem set, you’ll transition away from the regular languages to the context-free languages and to the realm of Turing machines. This will be ... your first foray beyond the limits of what computers can over hope to accomplish, and we hope that you find this as exciting as we do! As always, please feel free to drop by office hours or ask on Piazza if you have any questions. We'd be happy to help out. Good luck, and have fun! Due Friday, June 1st at 2:30PM.2 / 10 Problem One: Designing CFGs For each of the following languages, design a CFG for that language. Please use our online tool to design, test, and submit the CFGs in this problem. To use it, visit the CS103 website and click the “CFG Editor” link under the “Resources” header. You should only have one member from each team submit your grammars; tell us who this person is when you submit the rest of the problems through GradeScope. i. Given Σ = {a, b, c}, write a CFG for the language { w Σ* | ∈ w contains aa as a substring }. For example, the strings aa, baac, and ccaabb are all in the language, but aba is not. ii. Given Σ = {a, b}, write a CFG for the language { w Σ* | ∈ w is not a palindrome }, the language of strings that are not the same when read forwards and backwards. For example, aab ∈ L and baabab ∈ L, but aba ∉ L, bb ∉ L, and ε ∉ L. Don’t try solving this one by starting with the CFG for palindromes and making modifications to it. In general, there’s no way to mechanically turn a CFG for a language L into a CFG for the language L, since the context-free languages aren’t closed under complementation. However, the idea of looking at the first and last characters of a given string might be a good idea. iii. Let Σ be an alphabet containing these symbols: Ø ℕ { } , ∪ We can form strings from these symbols which represent sets. Here's some examples: Ø {{ℕ, Ø} {Ø}} ∪ {Ø, {Ø, {Ø}}} {Ø, ℕ} ℕ Ø ∪ ∪ ℕ {ℕ, Ø} ∪ {{{{ℕ}}}} {Ø} ℕ {ℕ} ∪ ∪ {} ℕ {Ø, Ø, Ø} {ℕ} {Ø, {}} Notice that some of these sets, like {Ø, Ø} are syntactically valid but redundant, and others like {} are syntactically valid but not the cleanest way of writing things. Here's some examples of strings that don't represent sets or aren't syntactically valid: ε ℕ, Ø, {Ø} {Ø }Ø{ {, ℕ} }} ℕ Ø{ℕ} { ℕ Ø }, { Ø, Ø, Ø, } {{} {,} {ℕ, , , Ø} Write a CFG for the language { w Σ* | ∈ w is a syntactically valid string representing a set }. When using the CFG tool, please use the letters n, u, and o in place of ℕ, , and Ø, ∪ respectively. Fun fact: The starter files for Problem Set One contain a parser that’s designed to take as input a string representing a set and to reconstruct what set that is. The logic we wrote to do that parsing was based on a CFG we wrote for sets and set theory. Take CS143 if you’re curious how to go from a grammar to a parser! Test your CFG thoroughly! In Fall 2017, a quarter of the submissions we received weren’t able to derive the string {Ø, Ø, Ø}.3 / 10 Problem Two: The Complexity of Addition This problem explores the following question: How hard is it to add two numbers? Suppose that we want to check whether x + y = z, where x, y, and z are all natural numbers. If we want to phrase this as a problem as a question of strings and languages, we will need to find some way to standardize our notation. In this problem, we will be using the unary number system, a number system in which the number n is represented by writing out n 1's. For example, the number 5 would be written as 11111, the number 7 as 1111111, and the number 12 as 111111111111. Given the alphabet Σ = {1, +, =}, we can consider strings encoding x + y = z by writing out x, y, and z in unary [Show More]

Last updated: 3 years ago

Preview 1 out of 10 pages