Mathematics > QUESTIONS & ANSWERS > Week 7 Assignment Hypothesis Test for the mean (All)

Week 7 Assignment Hypothesis Test for the mean

Document Content and Description Below

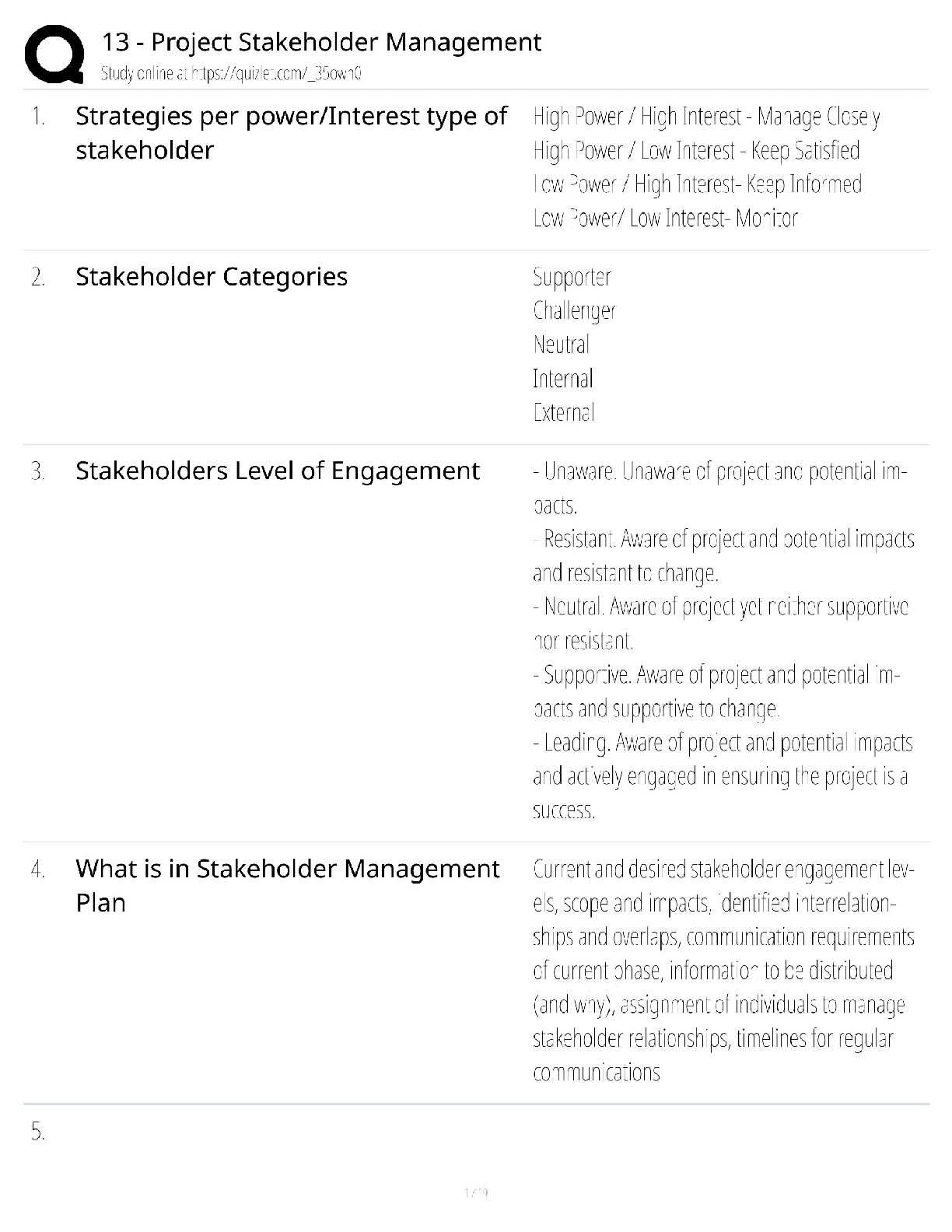
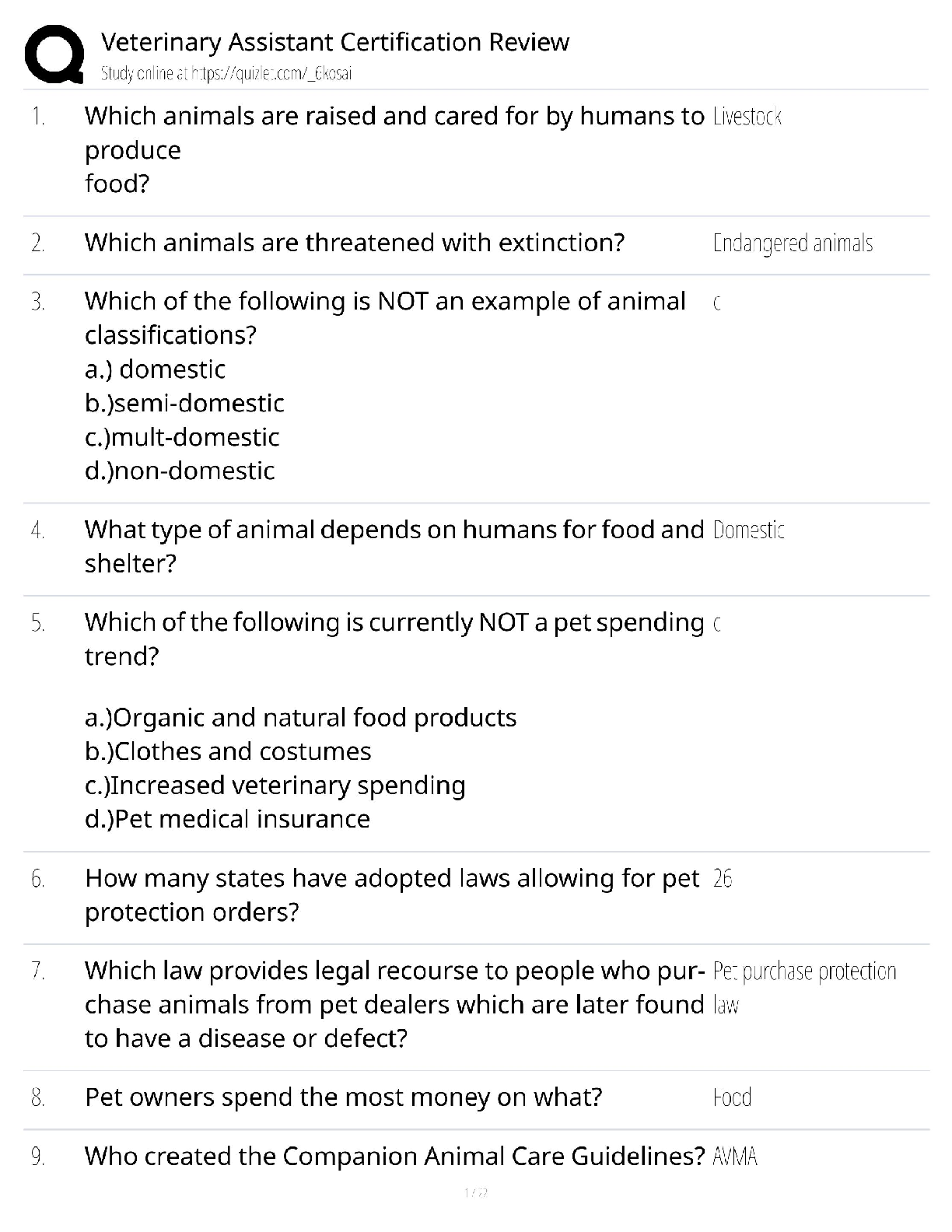
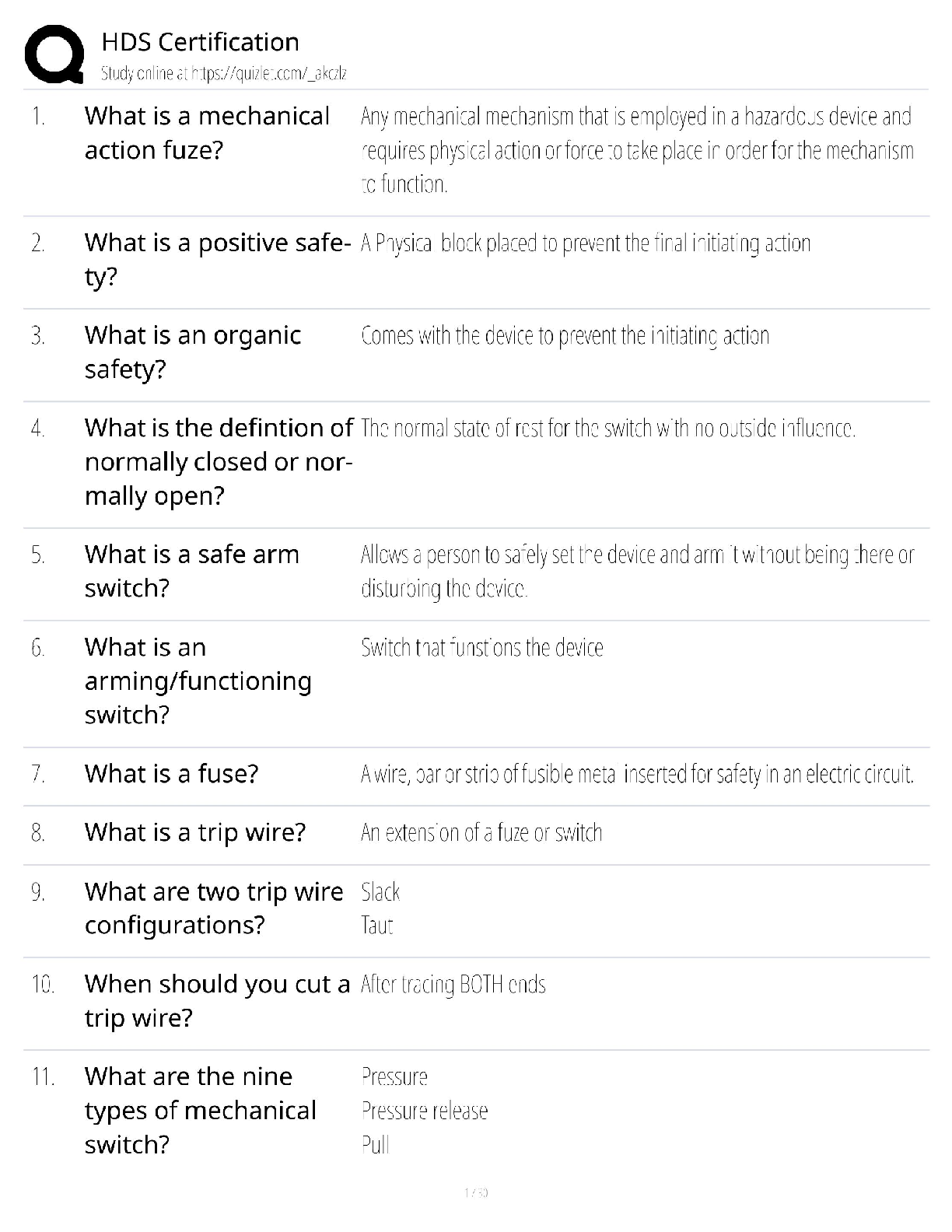
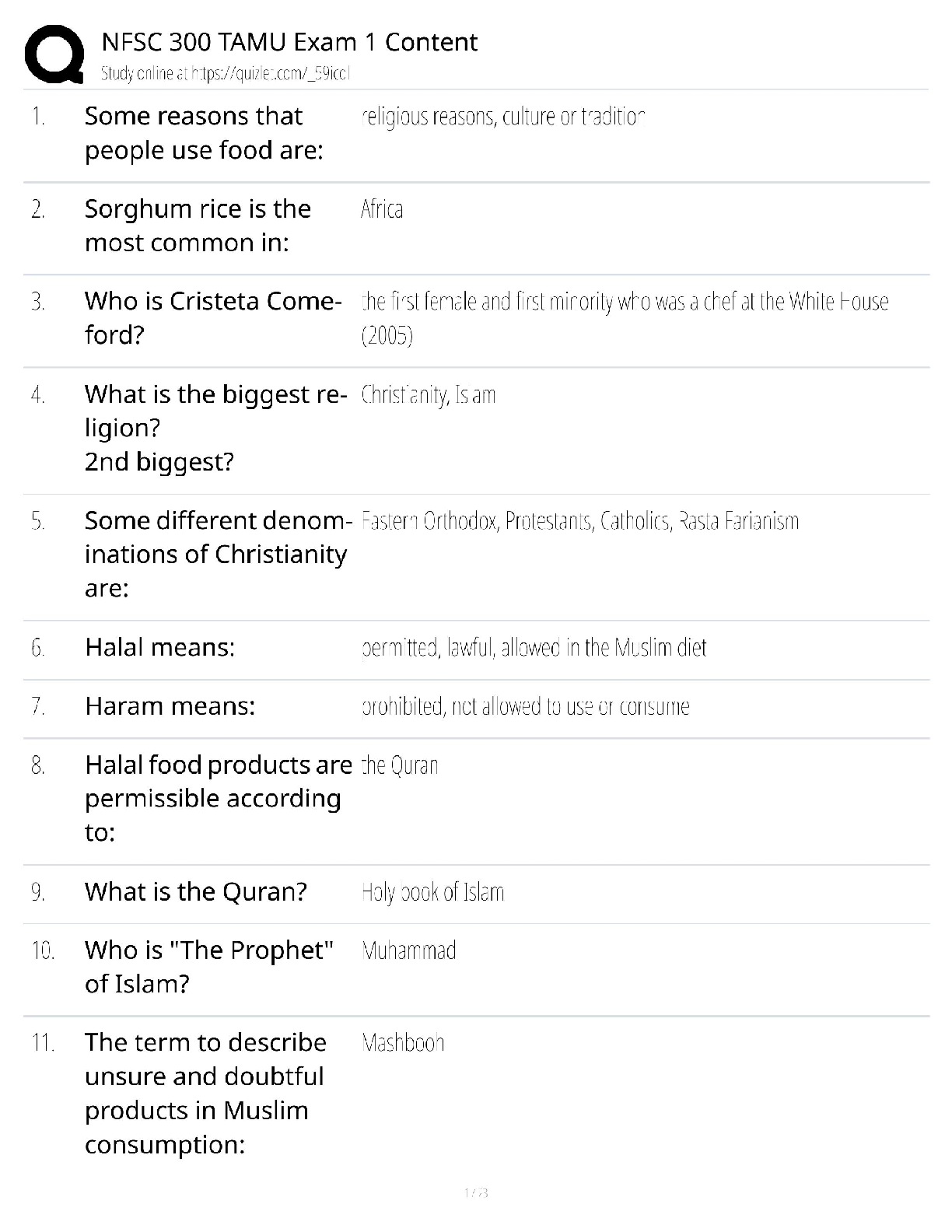
Compute the value of the test statistic (z-value) for a hypothesis test for one population mean with a known standard deviation Question Jamie, a bowler, claims that her bowling score is less than 1... 68 points, on average. Several of her teammates do not believe her, so she decides to do a hypothesis test, at a 1% significance level, to persuade them. She bowls 17 games. The mean score of the sample games is 155 points. Jamie knows from experience that the standard deviation for her bowling score is 19 points. • H0: μ≥168; Ha: μ<168 • α=0.01 (significance level) What is the test statistic (z-score) of this one-mean hypothesis test, rounded to two decimal places? Provide your answer: Test statistic = -2.82 Correct answers: The hypotheses were chosen, and the significance level was decided on, so the next step in hypothesis testing is to compute the test statistic. In this scenario, the sample mean score, x¯=155. The sample the bowler uses is 17 games, so n=17. She knows the standard deviation of the games, σ=19. Lastly, the bowler is comparing the population mean score to 168points. So, this value (found in the null and alternative hypotheses) is μ0. Now we will substitute the values into the formula to compute the test statistic: z0=x¯−μ0σn√=155−1681917√≈−134.608≈−2.82 So, the test statistic for this hypothesis test is z0=−2.82. Distinguish between one- and two-tailed hypotheses tests and understand possible conclusions Question Which graph below corresponds to the following hypothesis test? H0:μ≥5.9, Ha:μ<5.9 Answer Explanation ...................................................CONTINUED............................................ [Show More]

Last updated: 2 years ago

Preview 1 out of 19 pages

Buy Now

Instant download

We Accept: