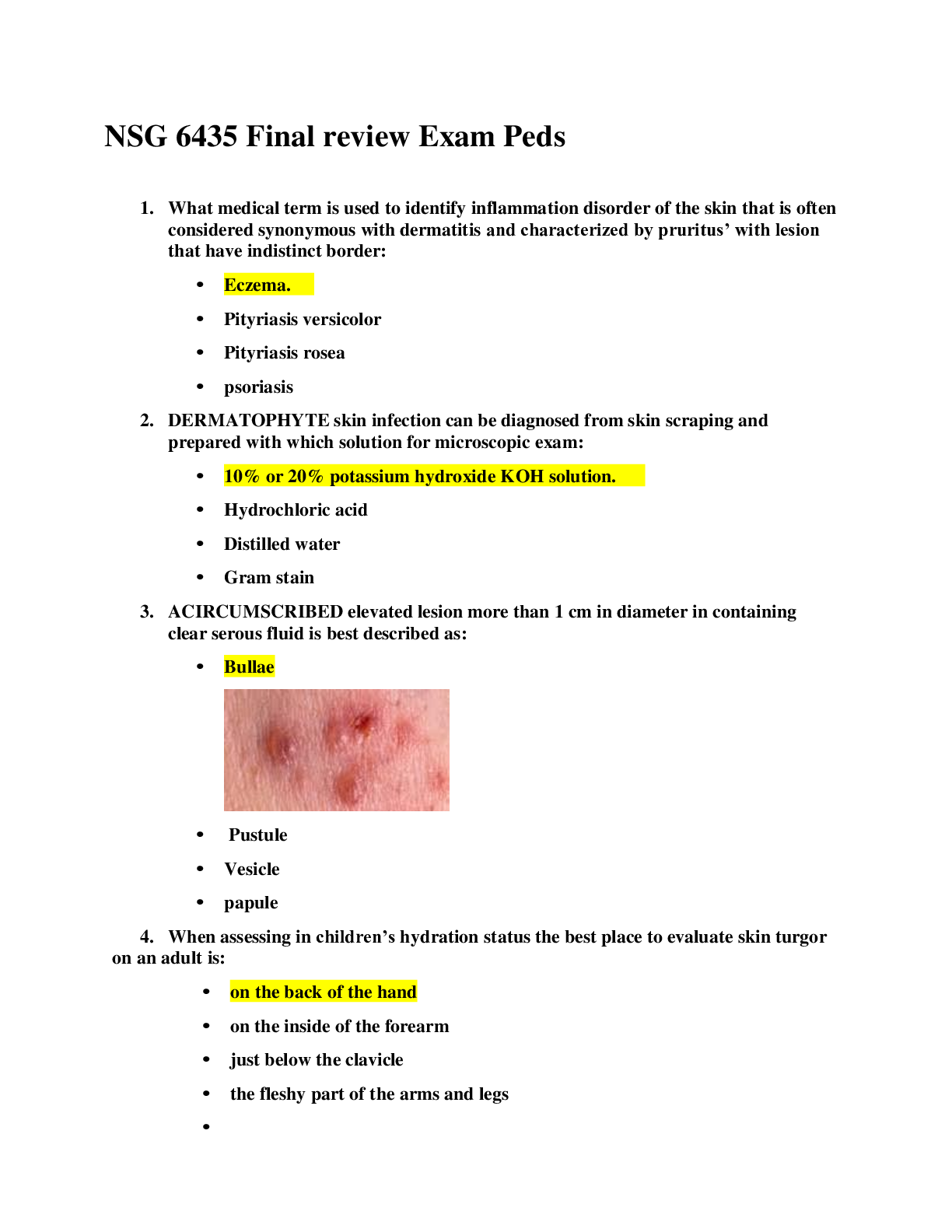
eBook Aristophanes: Cavalry 1st Edition By Robert Tordoff

$ 30

ACCT 301 Quiz 1 complete solution

$ 13.5

NR 325 MedSurg 2 Exam 1 Completed A

$ 10

Chapter 27: Female Genitourinary System_Jarvis Test Bank_Complete Solution

$ 16

Maryland CMIT 369 Discussion Questions Week 1

$ 11

Mathematics > QUESTIONS & ANSWERS > Collins Pure Maths 2 & 3 (All)

Collins Pure Maths 2 & 3

Document Content and Description Below

2 a (x + 1)(x + 2) = x2 + 3x + 2 b (x − 3)(x + 4) = x2 + x − 12 c (x − 2)(x − 3) = x2 − 5x + 6 d (x − 3)2 = x2 − 6x + 9 e (2x + 1)(x + 2) = 2x2 + 5x + 2 f (x + 1)(x + 2)(x + 3) = x3 ... + 6x2 + 11x + 6 3 a b a n a b n a b n a b 1 2 3 ... ( ) + = n n n +  1 2 n n 2 3 3    +   +   − − − + a b a n a b n a b n a b 1 2 3 ... ( ) + = n n n +  1 2 n n 2 3 3    +   +   − − − + x3 term = = 6 3 3 ! ! ! 23 3 x x 160 3 so the coeffi cient is 160 Using the factor theorem: Substitute x = − 2 into denominator 8 + 12 − 8 − 12 = 0 So (x + 2) is a factor. Using the factor theorem: Substitute x = 3 into denominator −27 + 27 + 12 − 12 = 0 So (3 − x) is a factor as coefficient of x3 is negative. Express the expression as partial fractions. The two different methods to split a rational function with linear factors in its denominator into partial fractions are substitution and equating coefficients. For partial fractions without repeated terms, the substitution method relies only on basic mathematical operations without the need for any algebraic manipulation, whereas the equating coefficients method results in the solving of simultaneous equations. For partial fractions with repeated terms, the substitution method relies on a combination of basic mathematical operations and the solving of simultaneous equations, whereas the equating coefficients method results in the solving of simultaneous equations with three unknowns [Show More]

Last updated: 3 years ago

Preview 1 out of 154 pages

Buy Now

Instant download

We Accept: