Georgia Institute Of Technology MGT 6203 Graded Homework 1 Solutions-verified A+

Document Content and Description Below

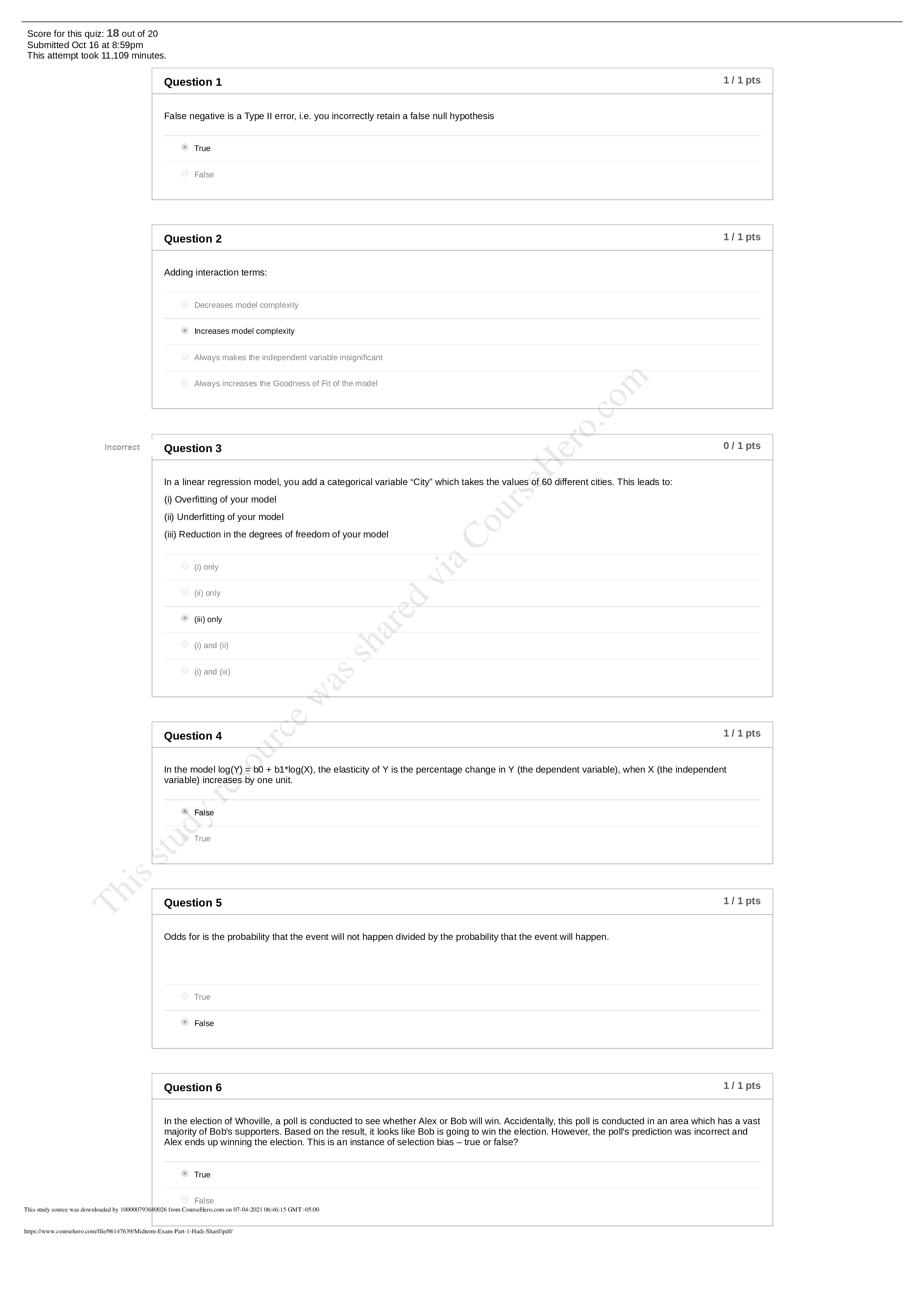
Graded Homework 1 Solution Manual Question 1. Choose the correct statement regarding the sum of residuals calculated using Ordinary Least Squares (OLS). Answer 1. (B) The sum of residuals will alw... ays be equal to zero if you include intercept term in your model and you are using OLS to estimate the coefficients. When an intercept is included in multiple linear regression for a data set with p points, the line is of the form: In OLS (Ordinary Least Square) Regression, the objective is to minimize the SSE (Sum of Squared Errors) to 0, which is obtained as follows: And to find all the betas, we differentiate all the above equation against all of betas individually including β0. We obtain ‘p+1’ equations to solve for all the ‘p+1’ betas. Differentiating against β0, we get: The above equation is responsible for ensuring that the sum of residuals is 0. Therefore, C and D are incorrect options. We now must decide between A and B. One form of regression under consideration is “Regression passing through Origin” (which is ideally not considered to be True OLS) which is a special case. Absence of intercept still means that the SSE is minimized, but it does not guarantee that SSE = 0. It is only when the intercept is included that the residuals sum up to 0. Thus, B is the correct option. One can think of the intercept as the catchall term, which provides for shifting the line of regression closer to or away from the X-axis (say the response terms are of the order 1000s, and thus the β0 value helps move the line of regression the said order, providing for finer tuned remaining betas). We understand that some ambiguity was observed regarding the forms of regression. Here, the question was designed keeping in mind the concept of the importance of the intercept term. While thetrue answer should be (B), we shall consider both (A) and (B) as the right choice. Question 2. Consider a simple linear regression model. Y ~ X. A fit for this model will be a line in the X-Y plane. Now suppose we fit a model for the opposite relationship: X ~ Y (that is, X dependent, and Y independent). This new model yields a new regression line in the X-Y plane. Which of the following statements are true about these two lines? Answer 2. (B) These lines will always intersect at the mean (Xmean, Ymean) If we have that y is a dependent variable on x, (and for their respective means ´ y and ´ x ), then the least squares regression Y ~ X line is given as: ( y−´ y)=CoV (x , y ) Var (x ) (x−x´ ) Similarly, the line for X ~ Y is given as: (x−´ x)=CoV (x , y ) Var ( y ) ( y−´ y) Clearly, these two lines meet at the means ´ y and ´ x . The above equation is obtained using the least square estimator method for estimating the values a and b while minimizing the residuals: The final line is y=a+bx and we find a and b using equations obtained by placing ∂ D(a , b) ∂ a = ∂ D(a ,b) ∂ b =0 which gives us a=´ y−b ´ x and b=CoV Var(x (x,)y ) We can also write a small piece of code to check the same: > mydata = read.csv(‘EDSAL.csv') > YregX <- lm(Salary~Experience, mydata) > summary(YregX) Call: lm(formula = Salary ~ Experience, data = mydata) Residuals: Min 1Q Median 3Q Max -73.00 -12.82 -1.18 13.32 60.85 2Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 29.4679 2.5673 11.48 <2e-16 *** Experience 3.0959 0.1113 27.81 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 24.05 on 298 degrees of freedom Multiple R-squared: 0.7218, Adjusted R-squared: 0.7209 F-statistic: 773.2 on 1 and 298 DF, p-value: < 2.2e-16 > XregY <- lm(Experience~Salary, mydata) > summary(XregY) Call: lm(formula = Experience ~ Salary, data = mydata) Residuals: Min 1Q Median 3Q Max -11.430 -4.867 -1.787 3.489 20.805 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -1.475177 0.841711 -1.753 0.0807 . Salary 0.233146 0.008385 27.806 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 6.601 on 298 degrees of freedom Multiple R-squared: 0.7218, Adjusted R-squared: 0.7209 F-statistic: 773.2 on 1 and 298 DF, p-value: < 2.2e-16 > plot(mydata$Experience, mydata$Salary) > abline(29.4679, 3.0959) > abline(1.475177/0.233146, 1/0.233146) > > mean(mydata$Experience) [1] 19.39333 > mean(mydata$Salary) [1] 89.50846 The graph produced is as follows (which meets at the mean of the Xs and Ys)> abline(29.4679, 3.0959) > abline(1.475177/0.233146, 1/0.233146) Kindly note that while plotting the two line on the same axis, the line from X ~ Y needs to be transformed to X-Y co-ordinate as shown above in the second line of code. Another point to n [Show More]

Last updated: 2 years ago

Preview 1 out of 19 pages