Data 100, Fall 2020
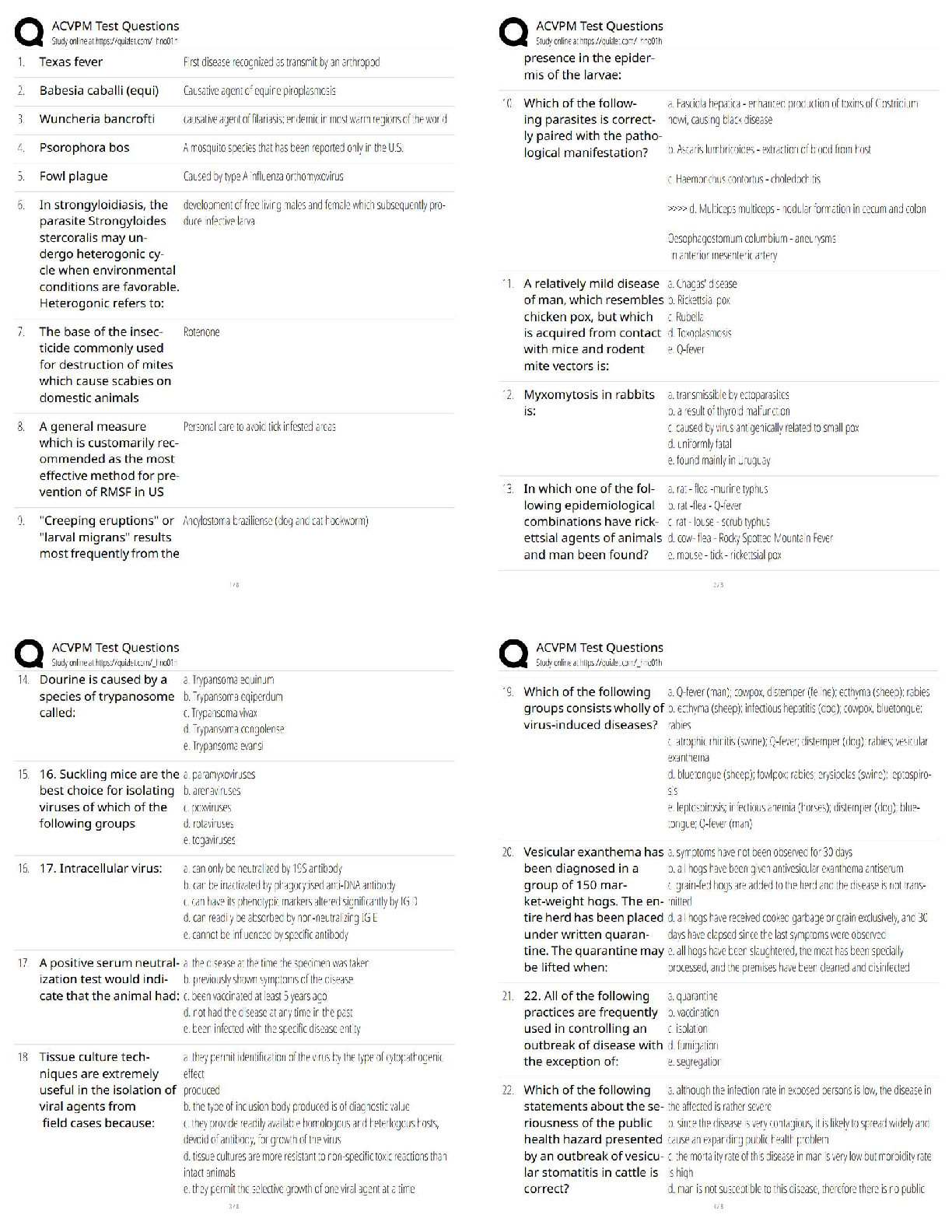
Homework 1
Due Date: Thursday, September 3, 11:59PM
Total Points: 24
Submission Instructions
You must submit this assignment to Gradescope by Thursday, September 3rd, at
11:59 PM. While Gradesco
...
Data 100, Fall 2020
Homework 1
Due Date: Thursday, September 3, 11:59PM
Total Points: 24
Submission Instructions
You must submit this assignment to Gradescope by Thursday, September 3rd, at
11:59 PM. While Gradescope accepts late submissions, you will not receive any credit for
a late submission if you do not have prior accommodations (e.g. DSP).
You can work on this assignment in any way you like.
• One way is to download this PDF, print it out, and write directly on these pages (we’ve
provided enough space for you to do so). Alternatively, if you have a tablet, you could
save this PDF and write directly on it.
• Another way is to use some form of LaTeX. Overleaf is a great tool.
• You could also write your answers on a blank sheet of paper.
Regardless of what method you choose, the end result needs to end up on Gradescope,
as a PDF. If you wrote something on physical paper (like options 1 and 3 above), you will
need to use a scanning application (e.g. CamScanner) in order to submit your work.
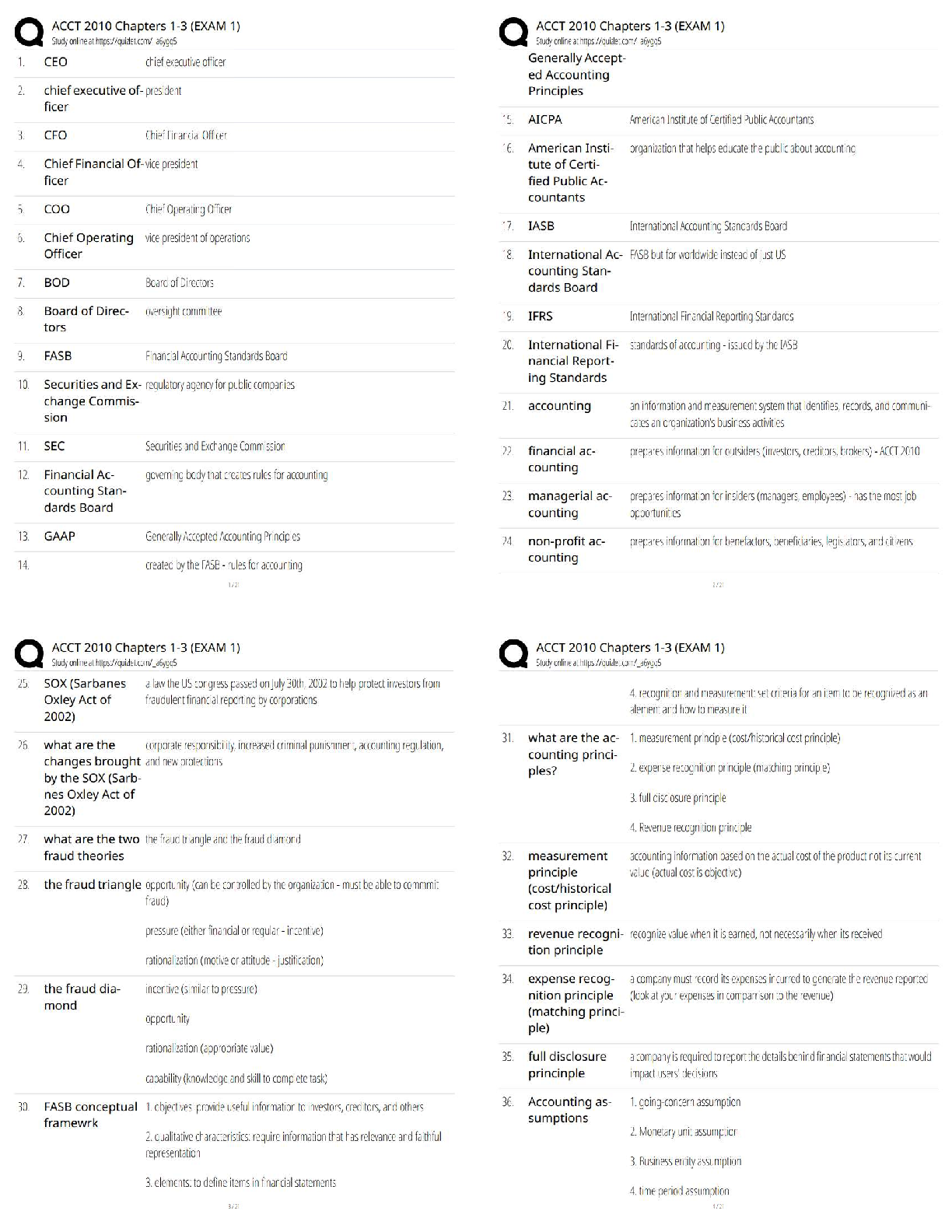
When submitting on Gradescope, you must assign pages to each question correctly (it
prompts you to do this after submitting your work). This significantly streamlines the
grading process for our tutors. Failure to do this may result in a score of 0 for any questions
that you didn’t correctly assign pages to. If you have any questions about the submission
process, please don’t hesitate to ask on Piazza.
Collaborators
Data science is a collaborative activity. While you may talk with others about the homework, we ask that you write your solutions individually. If you do discuss the assignments
with others please include their names at the top of your submission.
1
Homework 1 2
Preliminary: Sums
Here’s a recap of some basic algebra written in sigma notation. The facts are all just
applications of the ordinary associative and distributive properties of addition and multiplication, written compactly and without the possibly ambiguous ”...”. But if you are ever
unsure of whether you’re working correctly with a sum, you can always try writing Pn i=1 ai
as a1 + a2 + · · · + an and see if that helps.
• You can use any reasonable notation for the index over which you are summing, just
as in Python you can use any reasonable name in ‘for name in list‘. Thus Pn i=1 ai =
Pn k=1 ak.
• Pn i=1(ai + bi) = Pn i=1 ai + Pn i=1 bi
• Pn i=1 d = nd
• Pn i=1(cai + d) = c Pn i=1 ai + nd
We commonly use sigma notation to compactly write the definition of the arithmetic
mean (commonly known as the average): ¯ x = 1
n
(x1 + x2 + ... + xn) = 1
n
Pn i=1 xi.
Summations
1. (6 points) For each of the statements below, either prove that it is true by using the definitions above, or show that it is false by providing a counterexample. For our purposes,
each ai and xi is a real number. Hint: One way to prove something is to start with one
side of the equation, and manipulate it through a valid series of steps until it looks like
the other side of the equation.
(a)
Pn i=1 aixi
Pn i=1 ai = Pn i=1 xi (Assume Pn i=1 ai 6= 0)
(b) Pn i=1 a3xi = na3x¯
(c) Pn i=1 aixi = na¯x¯
qf ai xi E ai I i Xi True
E ai E ai
asXi a E I Yi recast EI ti
T
has5 True
E E aix Ei aiE xi nlklEI iailnlt.LI ixi
a
n
x
n a n 5 False
Homework 1 3
Calculus
2. (4 points) Let !(x) = 1
1 + e!x
.
(a) Show that !("x) = 1 " !(x).
(b) Show that the derivative can be written as:
d
dx!(x) = !(x)(1 " !(x))
Minimization
3. (3 points) Consider the function f(c) = n1 Pn i=1(xi " c)2. In this scenario, suppose that
our data points x1, x2, ..., xn are fixed, and that c is the only variable.
Using calculus, determine the value of c that minimizes f(c). You must justify that this
is indeed a minimum, and not a maximum.
OC x 1
ex
out e
e
OC H I 1 HI ext
e x Lte Y t Gex l o Cx
I Cite Y Y e
e
x l Te x
e
x e
ex it Ee x
e x
te x 2
of
L E 2CXi c
f c ht Enie Cy c 2 2C
y f y f
Jo f E 2C Yi 4 C Y JE 2
o E Xi C 270
O In E F Xi thE El C min
I c
Homework 1 4
Probability and Statistics
4. (4 points) Much of data analysis involves interpreting proportions – lots and lots of
related proportions. So let’s recall the basics. It might help to start by reviewing the
main rules from Data 8, with particular attention to what’s being multiplied in the
multiplication rule.
(a) The Pew Research Foundation publishes the results of numerous surveys, one of
which is about the trust that Americans have in groups such as the military, scientists, and elected o!cials to act in the public interest. A table in the article
summarizes the results.
Pick one of the options (1) or (2) to answer the question below; if you pick (1), tell
us what p is. Then, explain your choice.
The percent of surveyed U.S. adults who had a great deal of confidence in both
scientists and religious leaders
1. is equal to p%.
2. cannot be found with the information in the article.
(b) Toyota is one of most commonly owned makes of cars in our county (Alameda).
A car heading from Berkeley to San Francisco is pulled over on the freeway for
speeding. Suppose I tell you that the car is either a Toyota or a Lamborghini, and
you have to guess which of the two is more likely.
What would you guess, and why? Make some reasonable assumptions and explain
them (data scientists often have to do this), and justify your answer.
0
The percent who have a great deal of
confidence in scientists was 39 To
1740 for religious leaders Without more
info we cannot assume an overlap in
the two
groups
The Toyota is more likely bio first
of all as aforementioned the Toyota
is one of the most common cars On
the other hand the Lamborghini is
uncommon Therefore from the
numerous cars if one was parted over
it is more likely to be a Toyota
Homework 1 5
5. (3 points) Consider the following scenario:
Only 1% of 40-year-old women who participate in a routine mammography test have
breast cancer. 80% of women who have breast cancer will test positive, but 9.6% of
women who don’t have breast cancer will also get positive tests.
Suppose we know that a woman of this age tested positive in a routine screening. What
is the probability that she actually has breast cancer? (Note: You must show all of your
work, and also simplify your final answer to 3 decimal places.)
PC cancer pos
PCpost cancer P cancer
p pos
PCpost cancer P cancer t PC post no Peno
O 8 Co 01
O 8C O Ol t o 096 Co 99
O O 78
7 87
Homework 1 6
6. (2 points) Suppose we collected a sample of 200 students at UC Berkeley, and 150 of
them happened to be Canadian (so, if we were to select a student uniformly at random
from our sample, there is a 0.75 chance that they are Canadian).
For inferential purposes, we choose to bootstrap this sample 500,000 times. That is,
we simulate the act of re-sampling (with replacement) 200 students from our observed
sample, and each time we record the number of Canadians in our re-sample.
We provide a histogram of the sampling distribution below.
What is the standard deviation of the sampling distribution shown above? Select the
closest option below, and explain your answer.
A. 1.5
B. 6.1
C. 12.4
D. 10.1
Hint: While it is possible to calculate the answer, the histogram has all of the information
you need.
0
Looking at the histogram we can assume
normality and therefore apply the
68 95 99 7 rule which gives us the
Homework 1 7
Welcome Survey
7. (2 points) In order for the teaching sta↵ to best ensure you have a stellar Data 100
experience, we’ve put together a short welcome survey for us to get to know more about
you. When you have finished the survey, you will receive a codeword. Please
write this codeword as your answer to question 7.
I
Central beef overview
[Show More]





.png)

.png)
.png)
.png)


.png)