Mathematics > QUESTIONS & ANSWERS > Mid-Unit Assignment_ Dragon's Den - Virtual High School/Kells Academy - Advanced Functions MHF4U (All)

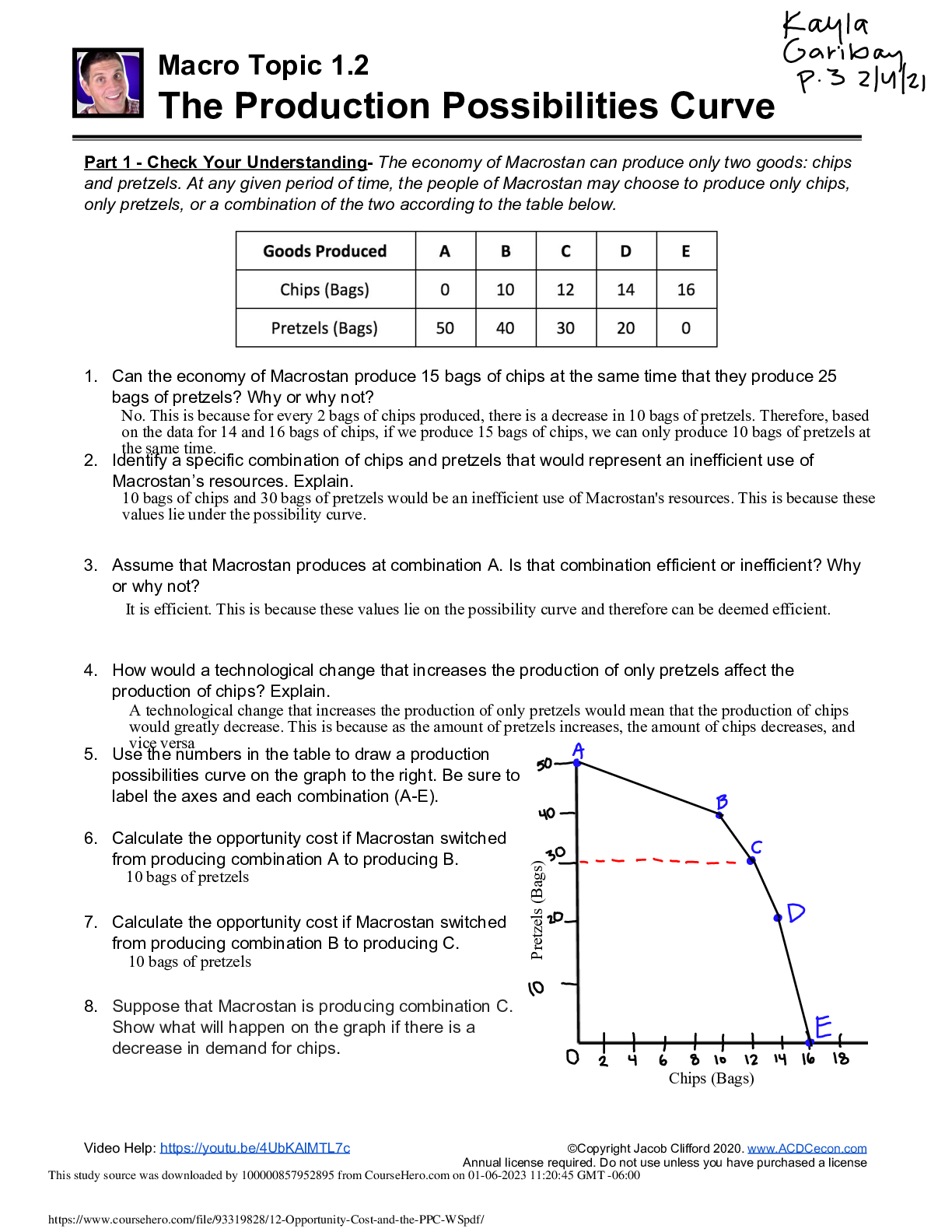
Mid-Unit Assignment_ Dragon's Den - Virtual High School/Kells Academy - Advanced Functions MHF4U

Document Content and Description Below

Virtual High School/Kells Academy Mr. Ken Stewart Advanced Functions MHF4U 01/16/2020 Question 2. The product that I am presenting to dragons is a new type of dry shampoo with new ingredients tha... t will make your hair look shinier and cleaner than the dry shampoos currently being produced. It is also an all organic shampoo, free of any harmful chemicals that will appeal to a larger group of consumers compared to the products currently being sold. Question 3. The dry shampoos are being produced currently at the cost of $4.5 in my laboratory. In other words, I am producing these products from home and I avoid paying more money on the rent. The function that represents the cost of producing dry shampoos is C(x)=mx which is C(x)=4.5x Question 4. Revenue is the amount of money that is made from the products sold without taking expenses into consideration. R(x) is the function used to calculate the amount of revenue for 500 Dry shampoos with a price of $9 per unit per month. R(x)= (price)*(number of products sold) R(x)= 9x a. If we consider that for every $0.15 increase in price for Dry Shampoos, 10 fewer units will be sold, we have to write R(x) with respect to that. The number of Dry shampoos sold is represented by (500-10x) and the price of the Dry shampoo is represented by (9+0.15x). Therefore R(x) is shown by: R(x)=(500-10x)(9+0.15x) b. c. According to the calculations shown below, the x-intercepts are x=-60 and x=50. The values obtained represent by how much the price has to increase so that the revenue will be zero. According to the last sentence, we need a valid (positive) number for price increase, which means x=-60 cannot be the price increase because the increase has to be a positive value. Therefore, x=50 is the only valid number that is left. This means that if the increase in the price of the product is 50 cents the profit that I make will be zero. Any value of x (increase in the price of my product) that is lower than 50, would mean that I make some profit. d. Maximum: the vertex of the function occurred at (-5,4537.5). Therefore, the maximum value that y can have is 4537.5. Which means I will have the maximum amount of revenue if the product is sold 5 cents cheaper than the curre [Show More]

Last updated: 2 years ago

Preview 1 out of 5 pages

Buy Now

Instant download

We Accept: