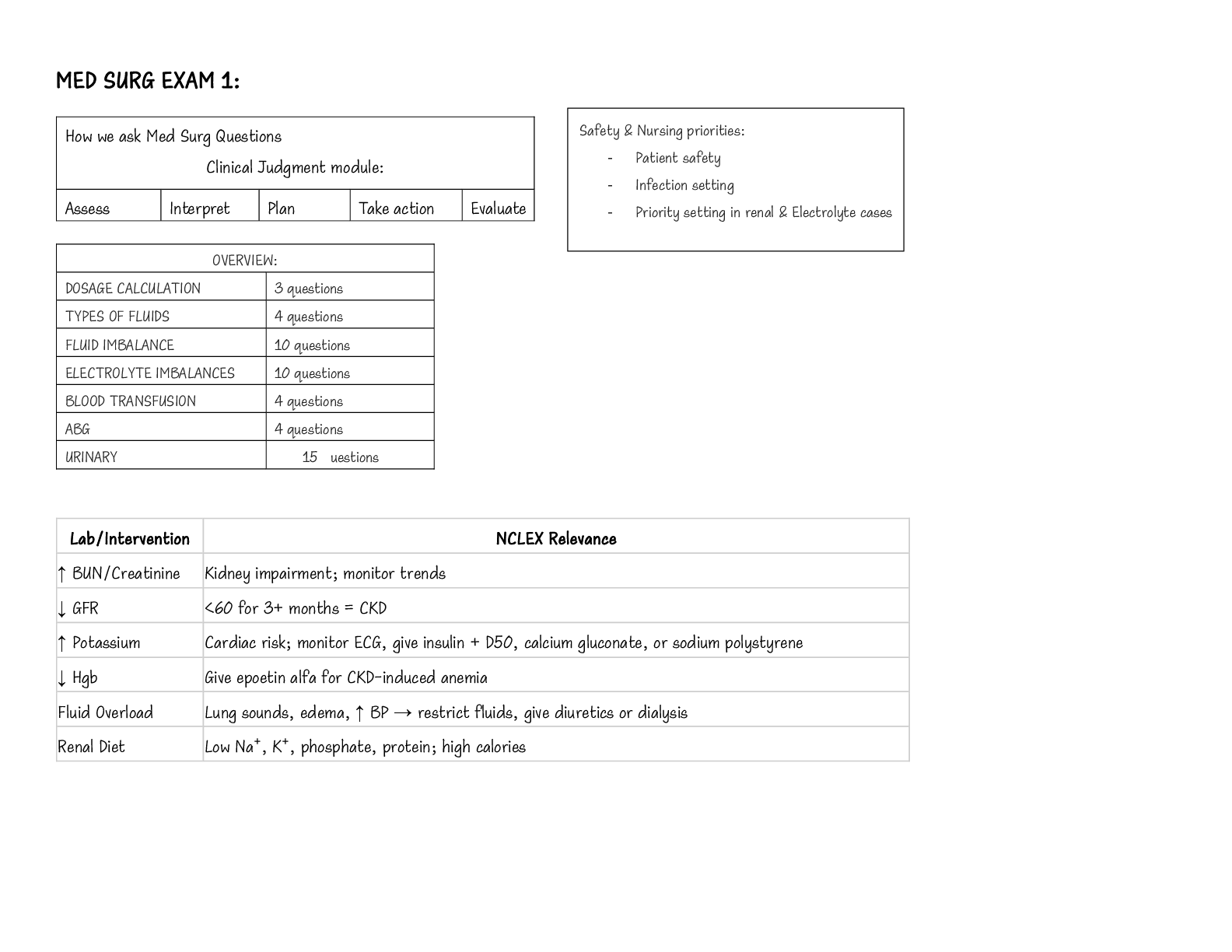
CONTENTS
UNIT – II
TWO DIMENSIONAL RANDOM VARIABLES
CHAPTER – I
• Definition of Two dimensional random variables
• Joint Distributions
� Distribution function
� Probability mass function
� Probability density fun
...
CONTENTS
UNIT – II
TWO DIMENSIONAL RANDOM VARIABLES
CHAPTER – I
• Definition of Two dimensional random variables
• Joint Distributions
� Distribution function
� Probability mass function
� Probability density function
• Marginal and Conditional Distributions
CHAPTER – II
• Covariance
• Correlation
• Regression
CHAPTER – III
• Transformation of Random VariablesTWO DIMENSIONAL RANDOM VARIABLES 2
UNIT – III
TWO DIMENSIONAL RANDOM VARIABLES
CHAPTER – I
INTRODUCTION TWO DIMENSIONAL RANDOM VARIABLES
In the last unit, we introduced the concept of a single random variable.We observed
that the various statistical averages or moments of the random variable like mean,
variance, standard deviation, skewness give an idea about the characteristics of the random
variable.But in many practical problems several random variables interact with each other
and frequently we are interested in the joint behaviour of these random variables.
For example, to know the health condition of a person, doctors measure many parameters
like height, weight, blood pressure, sugar level etc. We should now introduce techniques
that help us to determine the joint statistical properties of several random variables.The
concepts like distribution function, density function and moments that we defined for
single random variable can be extended to multiple random variables also.
Two Dimensional Random Variable
Let S be the sample space associated with a random experiment E.Let X=X(s) and
Y=Y(s) be two functions each assigning a real number to each outcomes s Є S. Then (X , Y) is
called a two dimensional random variable.
Note
(i)If the possible values of (X , Y) are finite or countable infinite, (X ,Y) is called a two
dimensional discrete random variable.
(ii)If (X , Y) can assume all values in a specified region R in the xy-plane, (X ,Y) is called a
two dimensional continuous random variable.TWO DIMENSIONAL RANDOM VARIABLES 3
Joint probability Mass Function (Discrete Case)
If (X,Y) is a two-dimensional discrete RV such that
P(X = xi , Y = yj) = pij , then pij is called the probability mass function of (X , Y) provided
pij ≥ 0 for all i and j.
(ii) p 1 ∑∑ ij =
i j
Joint probability Density Function (Continuous Case)
If (X,Y) is a two-dimensional continuous RV such that
x- ( , )
2 2 2 2
, f(x,y) is called the joint pdf of (X,Y),provided f(x,y)
satisfies the following conditions.
dx dx dy dy
p X x and y y f x y
dx dy then
≤ ≤ + − ≤ + =
(i) f (x , y) ≥ 0, for all (x , y) ∈ R, where R is the range space
( ) ( , ) d y = 1 .
R
i i f x y d x ∫∫
Note
{( ) D}= ( , ) . In particular
D
P X Y f x y dx dy < ∈ ∫∫
{ , } ( , )
d b
c a
P a X b c Y d f x y dx dy ≤ ≤ ≤ ≤ = ∫∫
Cumulative Distribution Function
If ( X , Y) is a two-dimensional RV (discrete or continuous ),
then F(x , y) = P{ X ≤ x and Y ≤ y } is called the cdf of (X,Y).
In the discrete case,TWO DIMENSIONAL RANDOM VARIABLES 4
( , ) = ∑∑
j i
F x y pij
In the continuous case,
( , ) ( , ) dy
y x
F x y f x y dx
−∞ −∞
= ∫ ∫
Properties of F (x , y)
[Show More]











.png)