Chamberlain College of Nursing Week 7 Math 225N Statistics Quiz Latest 2022

Document Content and Description Below

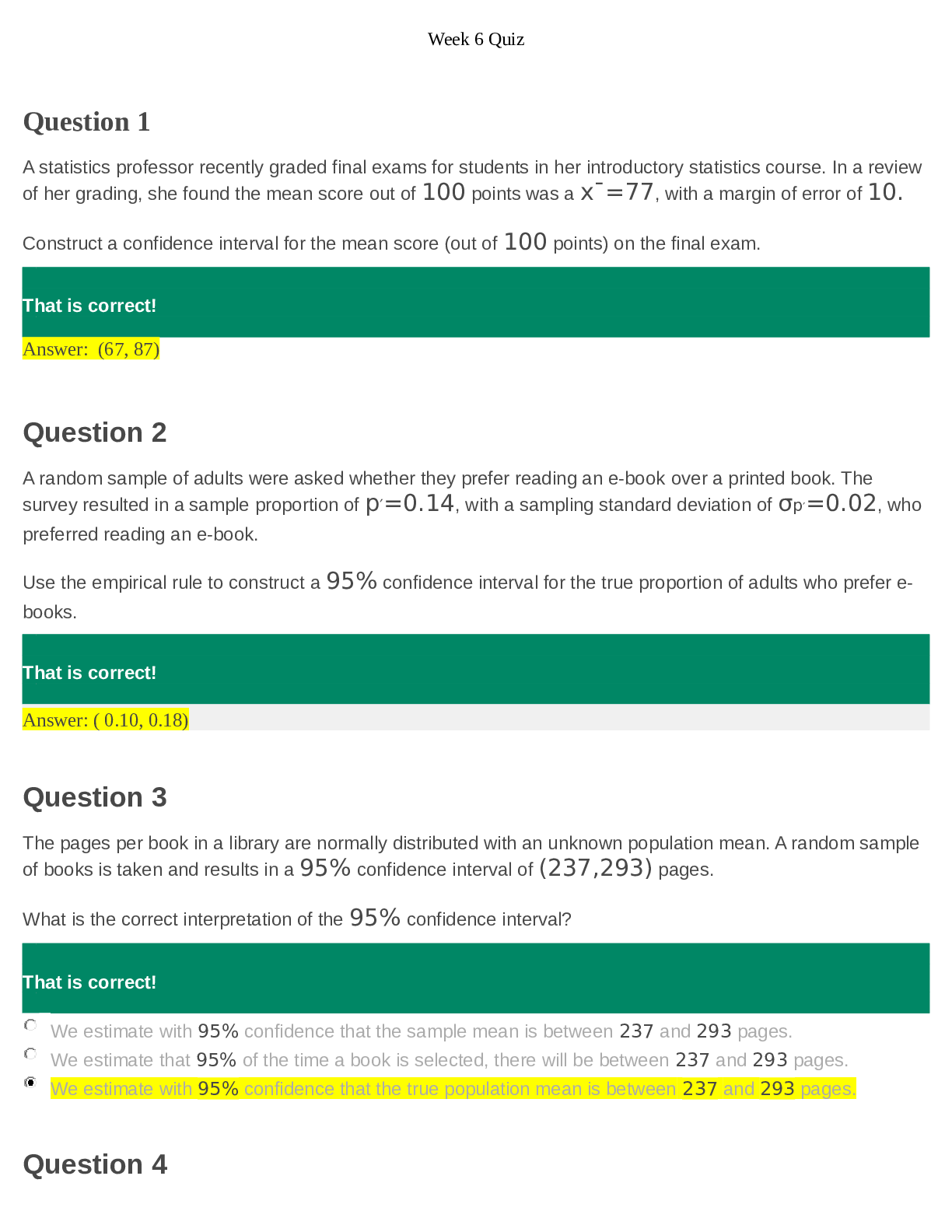
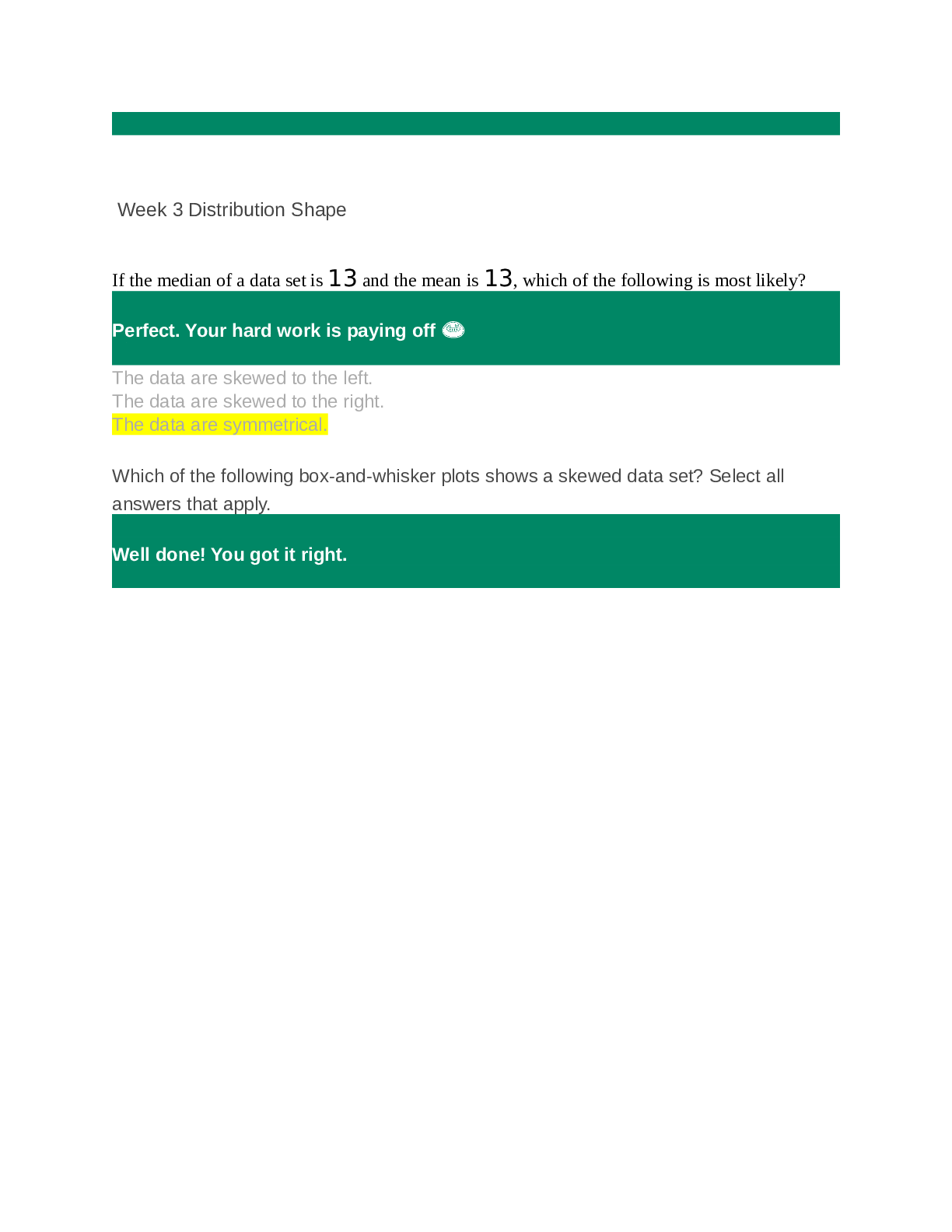
Week7 Assisgnment- Conducting a hypothesis test P-Value Approach Determine the p-value for a hypothesis test for the mean (population standard deviation known) Question What is the p-value of a two... -tailed one-mean hypothesis test, with a test statistic of z0=−1.73? (Do not round your answer; compute your answer using a value from the table below.) z−1.8−1.7−1.6−1.5−1.4 ....... Great work! That's correct. 0.084 Answer Explanation Correct answers:  0.084 The p-value is the probability of an observed value of z=1.73 or greater in magnitude if the null hypothesis is true, because this hypothesis test is two-tailed. This means that the p-value could be less than z=−1.73, or greater than z=1.73. This probability is equal to the area under the Standard Normal curve that lies either to the left of z=−1.73, or to the right of z=1.73. A normal curve is over a horizontal axis and is centered on 0. Two points are labeled negative 1.73 and 1.72 The area to the right of 1.73 and to the left of negative 1.73 is shaded. Using the Standard Normal Table given, we can see that the p-value that corresponds with z=−1.73 is 0.042, which is just the area to the left of z=−1.73. Since the Standard Normal curve is symmetric, the area to the right of z=1.73 is 0.042 as well. So, the p-value of this two-tailed one-mean hypothesis test is (2)(0.042)=0.084 Make a conclusion and interpret the results of a one-mean hypothesis test (population standard deviation known) using the P-Value Approach Question Mary, a javelin thrower, claims that her average throw is 61 meters. During a practice session, Mary has a sample throw mean of 55.5 meters based on 12 throws. At the 1% significance level, does the data provide sufficient evidence to conclude that Mary's mean throw is less than 61 meters? Accept or reject the hypothesis given the sample data below.  H0:μ=61 meters; Ha:μ<61 meters  α=0.01 (significance level)  z0=−1.99  p=0.0233 Great work! That's correct. Reject the null hypothesis because |−1.99|>0.01. Do not reject the null hypothesis because |−1.99|>0.01. Reject the null hypothesis because the p-value 0.0233 is greater than the significance level α=0.01. Do not reject the null hypothesis because the value of z is negative. Do not reject the null hypothesis because the p-value 0.0233 is greater than the significance level α=0.01. Answer Explanation Correct answer: Do not reject the null hypothesis because the p-value 0.0233 is greater than the significance level α=0.01. In making the decision to reject or not reject H0, if α>p-value, reject H0 because the results of the sample data are significant. There is sufficient evidence to conclude that H0 is an incorrect belief and that the alternative hypothesis, Ha, may be correct. If α≤p-value, do not reject H0. The results of the sample data are not significant, so there is not sufficient evidence to conclude that the alternative hypothesis, Ha, may be correct. In this case, α=0.01 is less than or equal to p=0.0233, so the decision is to not reject the null hypothesis. Make a conclusion and interpret the results of a one-mean hypothesis test (population standard deviation known) using the P-Value Approach Question Marty, a typist, claims that his average typing speed is 72 words per minute. During a practice session, Marty has a sample typing speed mean of 84 words per minute based on 12 trials. At the 5% significance level, does the data provide sufficient evidence to conclude that his mean typing speed is greater than 72 words per minute? Accept or reject the hypothesis given the sample data below. H0:μ≤72 words per minute; Ha:μ>72 words per minute α=0.05 (significance level) z0=2.1 p=0.018 Select the correct answer below: Do not reject the null hypothesis because 2.1>0.05. Do not reject the null hypothesis because the value of z is positive. Reject the null hypothesis because 2.75>0.05. Reject the null hypothesis because the p-value 0.018 is less than the significance level α=0.05. Do not reject the null hypothesis because the p-value 0.018 is less than the significance level α=0.05. Perfect. Your hard work is paying off � Determine the p-value for a hypothesis test for the mean (population standard deviation known) Question What is the p-value of a two-tailed one-mean hypothesis test, with a test statistic of z0=0.27? (Do not round your answer; compute your answer using a value from the table below.) z0.10.20.30.40.5............ Well done! You got it right. 0.788 The p-value is the probability of an observed value of z=0.27 or greater in magnitude if the null hypothesis is true, because this hypothesis test is two-tailed. This means that the p-value could be less than z=−0.27, or greater than z=0.27. This probability is equal to the area under the Standard Normal curve that lies either to the left of z=−0.27, or to the right of z=0.27 [Show More]

Last updated: 2 years ago

Preview 1 out of 10 pages