CES EduPack – Design Problem 2
Using Level 2, with ‘Metric Units’ and ‘Use Display Units for Temperature’:
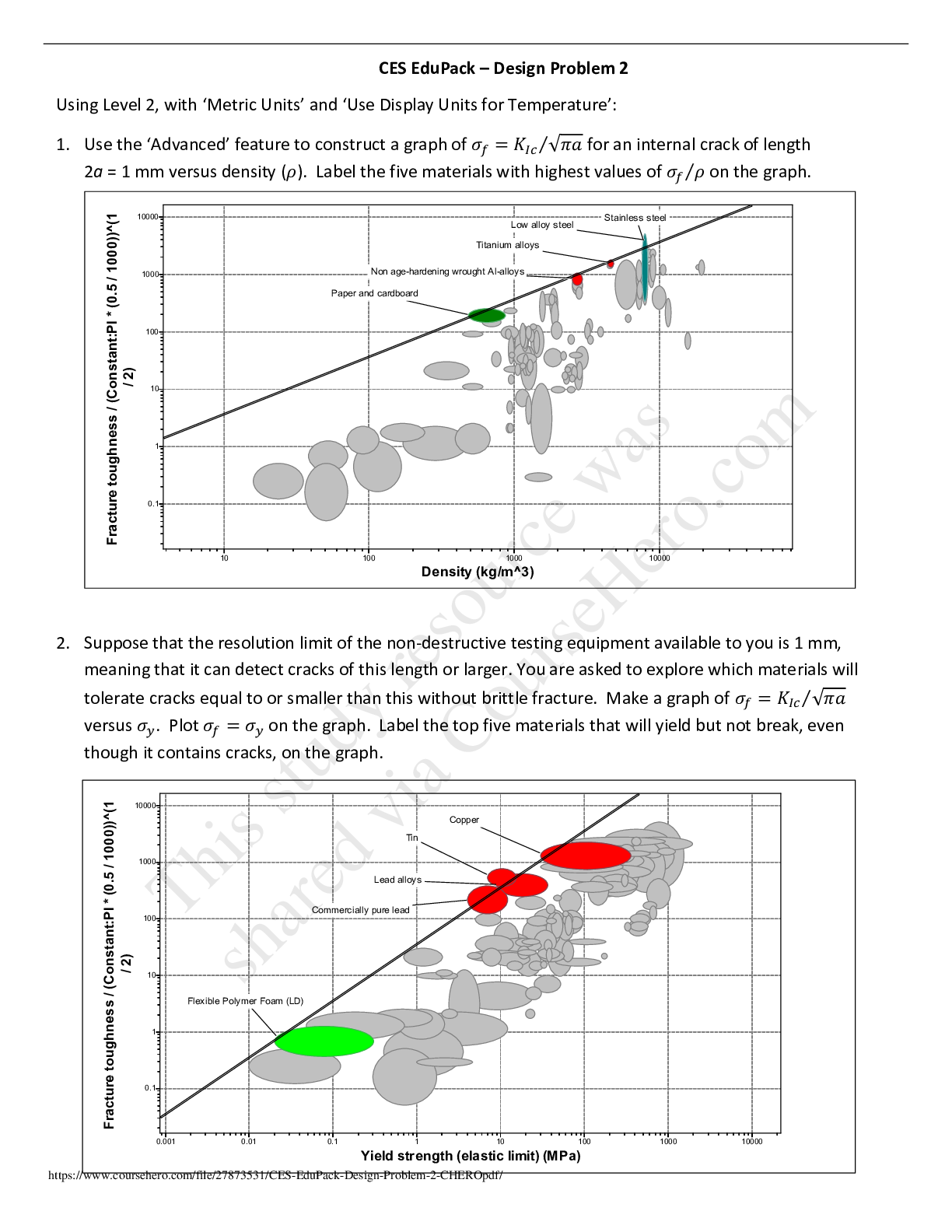
1. Use the ‘Advanced’ feature to construct a graph of ? = ?ூ⁄√?? for an internal crack of length
2a = 1 mm v
...
CES EduPack – Design Problem 2
Using Level 2, with ‘Metric Units’ and ‘Use Display Units for Temperature’:
1. Use the ‘Advanced’ feature to construct a graph of ? = ?ூ⁄√?? for an internal crack of length
2a = 1 mm versus density (?). Label the five materials with highest values of ?⁄? on the graph.
2. Suppose that the resolution limit of the non-destructive testing equipment available to you is 1 mm,
meaning that it can detect cracks of this length or larger. You are asked to explore which materials will
tolerate cracks equal to or smaller than this without brittle fracture. Make a graph of ? = ?ூ⁄√??
versus ?
௬. Plot ? = ?௬ on the graph. Label the top five materials that will yield but not break, even
though it contains cracks, on the graph.
Density (kg/m^3)
10 100 1000 10000
Fracture toughness / (Constant:PI * (0.5 / 1000))^(1
/ 2)
0.1
1
10
100
1000
10000
Paper and cardboard
Non age-hardening wrought Al-alloys
Titanium alloys
Low alloy steel
Stainless steel
Yield strength (elastic limit) (MPa)
0.001 0.01 0.1 1 10 100 1000 10000
Fracture toughness / (Constant:PI * (0.5 / 1000))^(1
Flexible Polymer Foam (LD)
Copper
Commercially pure lead
Tin
Lead alloys
This study resource was
shared via CourseHero.com3. Create a Yield Strength v. Density graph. Apply the following Limits: Yield Strength greater than 300 MPa,
minimum elongation of 5%, and Density less than 3,000 kg/m3. Then use the ‘Properties’ button to modify
the axes so that the x-axis has a range of 1,000 – 10,000 kg/m3 and the y-axis has a range of 10 – 1,000
MPa. Finally, label the remaining materials on the graph.
4. Valve springs for high performance automobile engines must be light to minimize inertial loads, since part
of their mass moves with the valves. At high engine speeds the valves, if heavy, bounce out of contact with
the valve itself (‘valve bounce’), impeding the flow of gas into and out of the combustion chamber. The
energy stored per unit volume is equivalent to modulus of resilience of a material, i.e., ? = ?௬ଶ⁄(2?). The
energy stored per unit weight is then, ? = ?௬ଶ⁄(2??). So the best choices are materials with the highest
value of ? = ?
ଶ௬
⁄(2??). Make a bar graph with this quantity on the y-axis, and label the top five ‘best’
materials on the graph. NOTE: In order for the material to be stiff enough, it must have E > 20 GPa. In
addition, engine operation temperatures can reach 200°C. Therefore, use a Limit of E > GPa, and a Limit of
Maximum Service Temperature minimum of 200°C.
Density (kg/m^3)
1000 2000 5000 10000
Yield strength (elastic limit) (MPa)
10
100
1000
Cast Al-alloys
Wrought magnesium alloys
Age-hardening wrought Al-alloys
Aluminum/Silicon carbide composite
(Yield strength (elastic limit)^2) / (2 * Density * Young's
modulus)
CFRP, epoxy matrix (isotropic)
Titanium alloys
Wrought magnesium alloys
Age-hardening wrought Al-alloys
Nickel-based superalloys
[Show More]