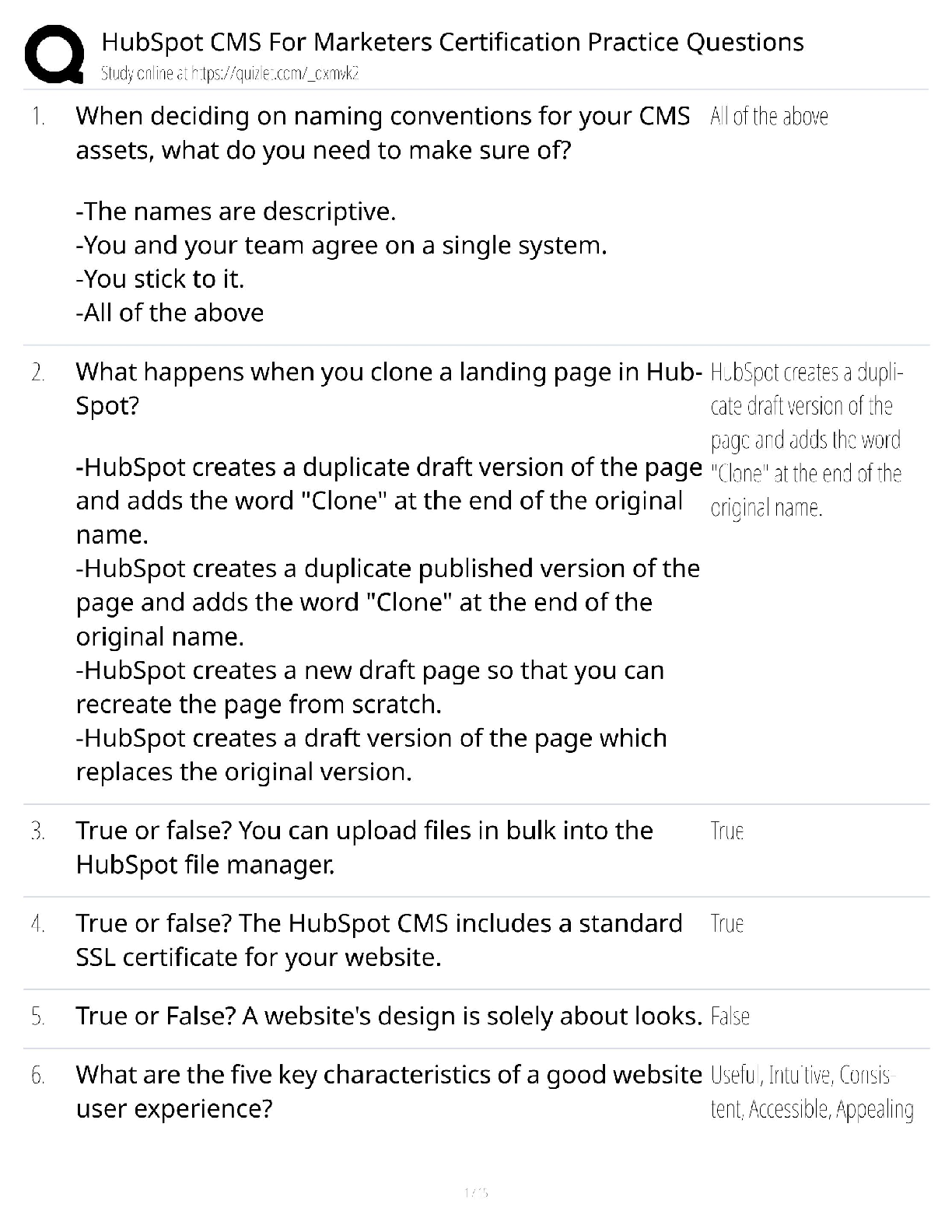
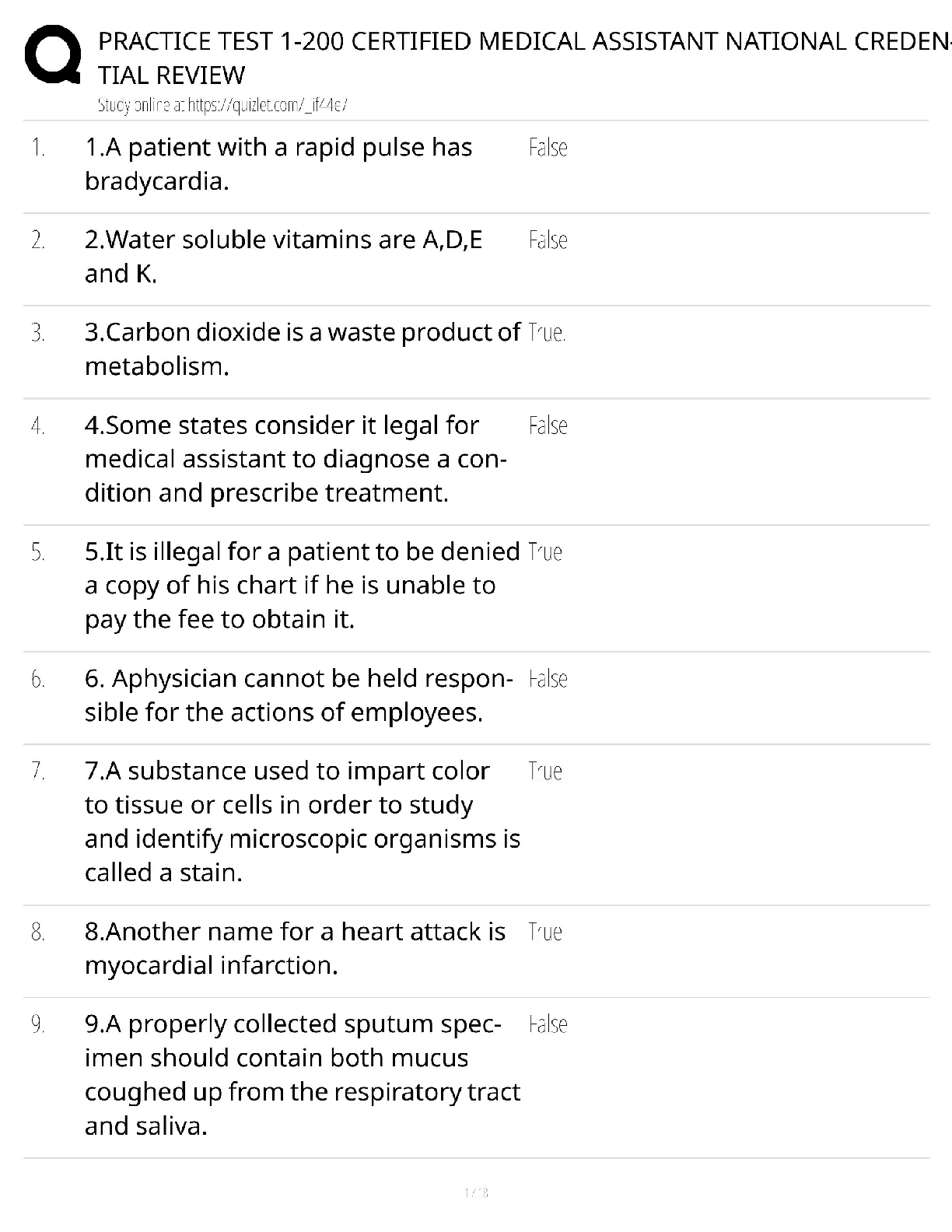
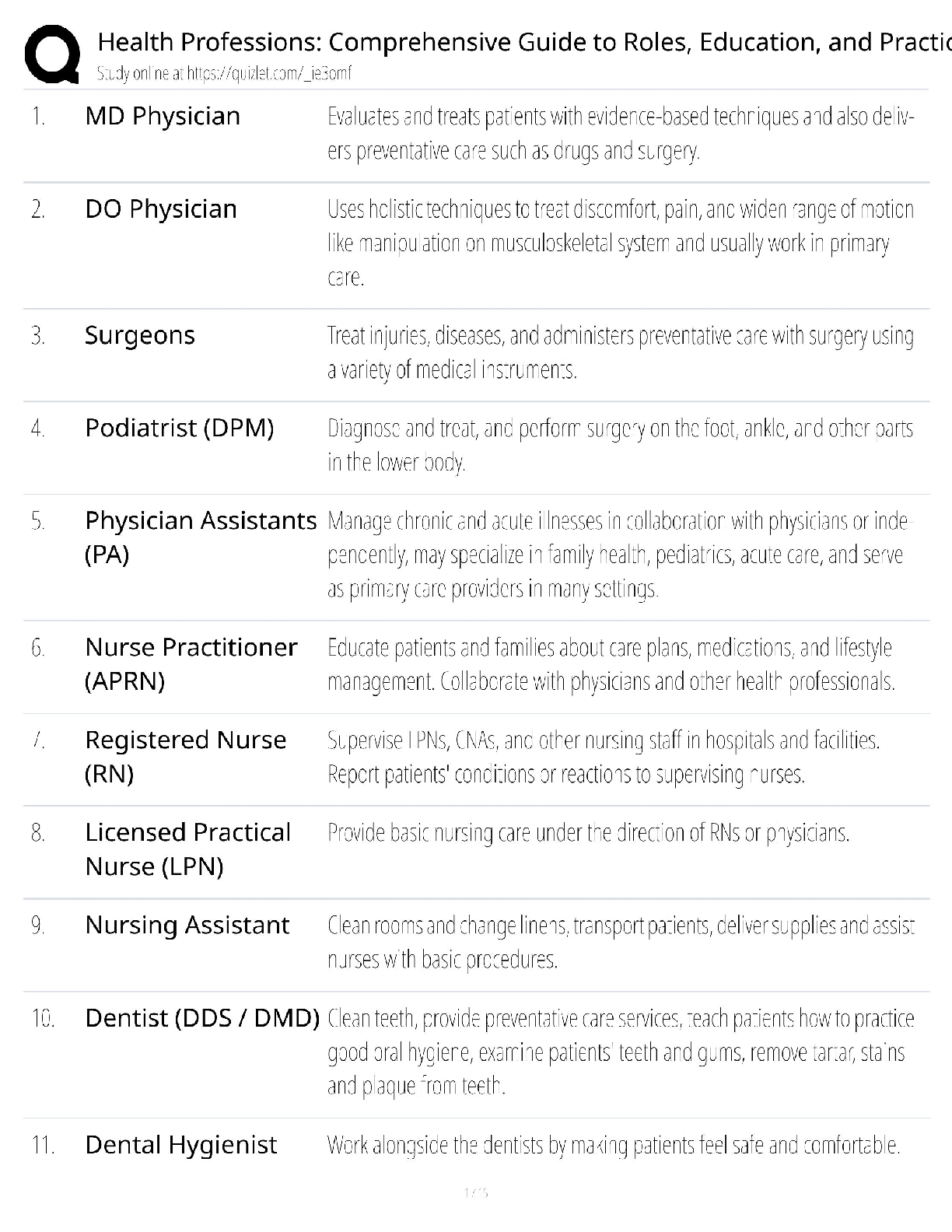
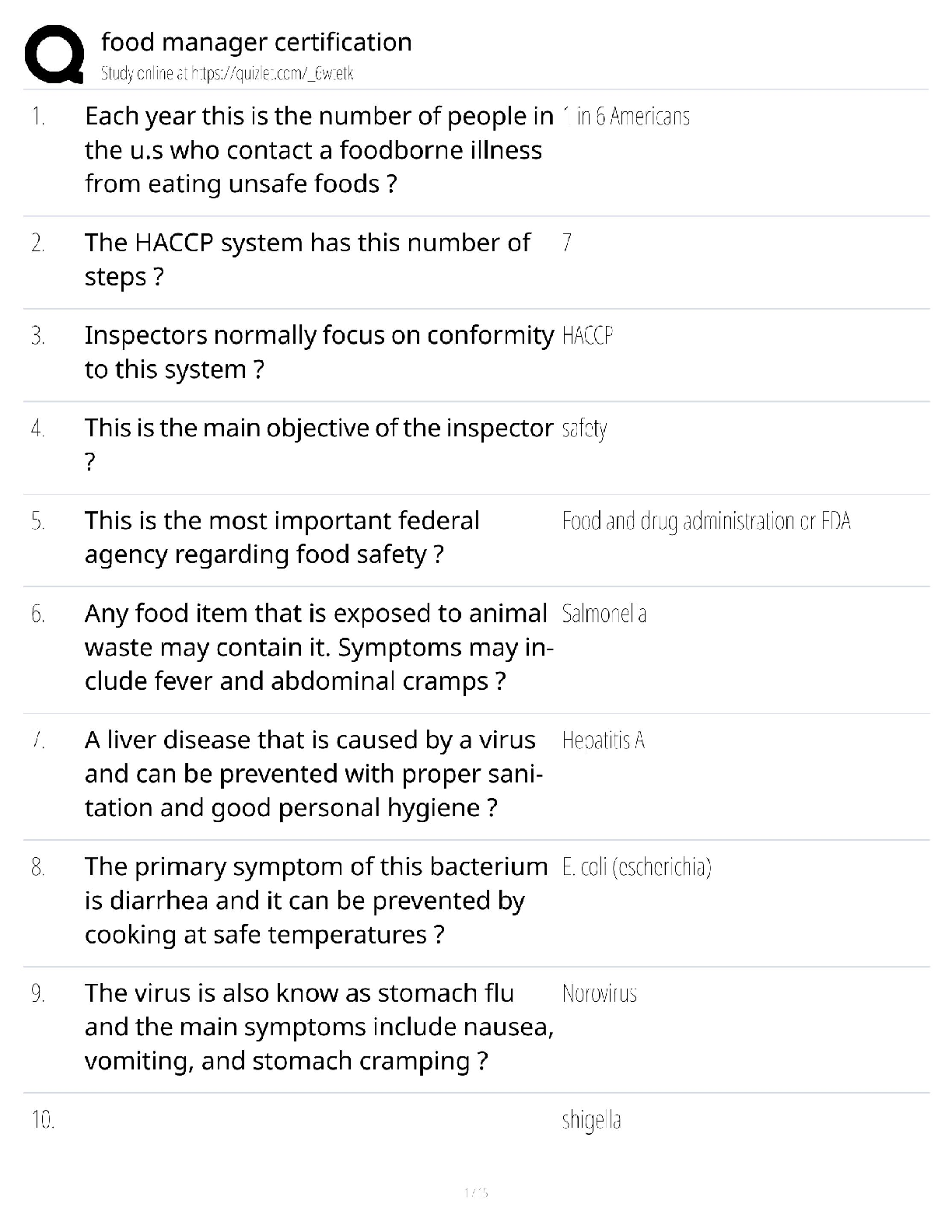
Information Technology > QUESTIONS & ANSWERS > Georgia Tech Homework 2 Question 3.1, 100% Graded A+ (All)
Georgia Tech Homework 2 Question 3.1, 100% Graded A+
Document Content and Description Below
Homework 2 Question 3.1 Using the same data set (credit_card_data.txt or credit_card_data-headers.txt) as in Question 2.2, use the ksvm or kknn function to find a good classifier: (a) using cross- ... validation (do this for the k-nearest-neighbors model; SVM is optional); and Using leave-one-out crossvalidation with different kernel for classification data <- read.csv("credit_card_data-headers.txt", header = TRUE, sep = "") # Splitting data for training (70%) and validating (30%) number_of_data_points <- nrow(data) training_sample <- sample(number_of_data_points, size = round(number_of_data_points * 0.7)) training_data <- data[training_sample,] validating_data <- data[-training_sample,] kmax <- 100 model <- train.kknn(R1~., training_data, kmax = kmax, scale = TRUE, kernel = c("rectangular", "triangular", "epanechnikov", "gaussian", "rank", "optimal")) model ## ## Call: ## train.kknn(formula = R1 ~ ., data = training_data, kmax = kmax, kernel = c("rectangular", "triang ## ## Type of response variable: continuous ## minimal mean absolute error: 0.1957787 ## Minimal mean squared error: 0.107393 ## Best kernel: gaussian ## Best k: 41 pred <- predict(model, validating_data[,-11]) accuracy <- sum(as.integer(round(pred) == validating_data[,11])) / nrow(validating_data) # Accuracy on validation data cat("Best accuracy for validation data is", accuracy, " for K value of", model$best.parameters$k, "\n\n") ## Best accuracy for validation data is 0.8469388 for K value of 41 (b) splitting the data into training, validation, and test data sets (pick either KNN or SVM; the other is optional). data <- read.csv("credit_card_data-headers.txt", header = TRUE, sep = "") # spliting data into training: 60%, validating: 20% and testing: 20% 1number_of_data_points <- nrow(data) training_sample <- sample(number_of_data_points, size = round(number_of_data_points * 0.6)) training_data <- data[training_sample,] non_training_data <- data[-training_sample,] number_of_non_training_data_points = nrow(non_training_data) validating_sample <- sample(number_of_non_training_data_points, size = round(number_of_non_training_data_points * 0.5)) validating_data <- non_training_data[validating_sample,] testing_data <- non_training_data[-validating_sample,] # Using kknn for crossvalidation Ks <- seq(1, 100) bestK <- 0 bestAcuracy <- 0 bestModel <- NULL for(k in Ks) { model <- kknn(R1~., training_data, validating_data, k = k, scale = TRUE) pred <- round(predict(model)) accuracy <- sum(pred == validating_data[,11]) / nrow(validating_data) # Keeping the best accuracy data for later use if(accuracy > bestAcuracy) { bestAcuracy <- accuracy bestK <- k bestModel <- model } } # Best K and it accuracy on validation data cat("Best K value is", bestK, "with accuracy of", bestAcuracy, "\n\n") ## Best K value is 11 with accuracy of 0.870229 # Running the test data with best K value model <- kknn(R1~., training_data, testing_data, k = bestK, scale = TRUE) pred <- round(predict(model)) accuracy <- sum(pred == testing_data[,11]) / nrow(testing_data) # Accuracy of test data with best K cat("Acuracy with K value of", bestK, "on test data is", accuracy, "\n\n") ## Acuracy with K value of 11 on test data is 0.8549618 Question 4.1 Describe a situation or problem from your job, everyday life, current events, etc., for which a clustering model would be appropriate. List some (up to 5) predictors that you might use. One of the key revenue generator for our e-commerce business is the recommendation based online sales. In order to make product recommendation, we need to group our online visitors and returing customers into various groups. Some of the common predictors we use are: 21. Average money spent on each transaction by returning customers through our website helps us to understand customer budget. An >example is to group customers into $1-$25, $26-$100, $101-$200, etc. 2. Search history helps us to group our online visitors based on the keywords they use to search our inventory. 3. Customer location is another important predictor. A good use case is when a customer shopping from New York city, NY vs someone from Miami, FL in January, only one of them is more likely to buy snow gear. 4. Previously purchased product brands gives us a good idea about quality and brand our various customers may prefer. 5. Age group is also a major predictor for different product selection. Question 4.2 The iris data set iris.txt contains 150 data points, each with four predictor variables and one categorical response. The predictors are the width and length of the sepal and petal of flowers and the response is the type of flower. The data is available from the R library datasets and can be accessed with iris once the library is loaded. It is also available at the UCI Machine Learning Repository (https://archive.ics.uci.edu/ml/datasets/Iris ). The response values are only given to see how well a specific method performed and should not be used to build the model. Use the R function kmeans to cluster the points as well as possible. Report the best combination of predictors, your suggested value of k, and how well your best clustering predicts flower type. iris <- read.csv("iris.txt", header = TRUE, sep = "") # extract all columns except last one data <- scale(iris[,-5]) # Using elbow method find to best number of clusters Ks = 1:20 wss <- rep(0, length(Ks)) for(k in Ks) { wss[k] <- kmeans(data, centers=k, nstart = 10)$tot.withinss } plot(Ks, wss, type="b", xlab="Number of clusters", ylab="Total WSS") 35 10 15 20 100 200 300 400 500 600 Number of clusters Total WSS From the plot we can see that the optimal K is 3 Now lets run kmeans with K=3 on all the combinations of predictors to find the best combination for clustering data_for_sepal_dim <- data[, c("Sepal.Length", "Sepal.Width")] cluster_for_sepal_dim <- kmeans(data_for_sepal_dim, 3, nstart = 10) table(cluster_for_sepal_dim$cluster, iris$Species) ## ## setosa versicolor virginica ## 1 1 36 19 ## 2 49 0 0 ## 3 0 14 31 data_for_sepal_length_petal_length <- data[, c("Sepal.Length", "Petal.Length")] cluster_for_sepal_length_petal_length <- kmeans(data_for_sepal_length_petal_length, 3, nstart = 10) table(cluster_for_sepal_length_petal_length$cluster, iris$Species) ## [Show More]
Last updated: 3 years ago
Preview 1 out of 7 pages

Buy this document to get the full access instantly
Instant Download Access after purchase
Buy NowInstant download
We Accept:

Also available in bundle (1)
Click Below to Access Bundle(s)

GEORGIA TECH BUNDLE, ALL ISYE 6501 EXAMS, HOMEWORKS, QUESTIONS AND ANSWERS, NOTES AND SUMMARIIES, ALL YOU NEED
GEORGIA TECH BUNDLE, ALL ISYE 6501 EXAMS, HOMEWORKS, QUESTIONS AND ANSWERS, NOTES AND SUMMARIIES, ALL YOU NEED
By bundleHub Solution guider 3 years ago
$60
59
Reviews( 0 )
$6.00
Can't find what you want? Try our AI powered Search
Document information
Connected school, study & course
About the document
Uploaded On
Sep 03, 2022
Number of pages
7
Written in
All
Seller

Reviews Received
Additional information
This document has been written for:
Uploaded
Sep 03, 2022
Downloads
0
Views
179