ISYE 6501
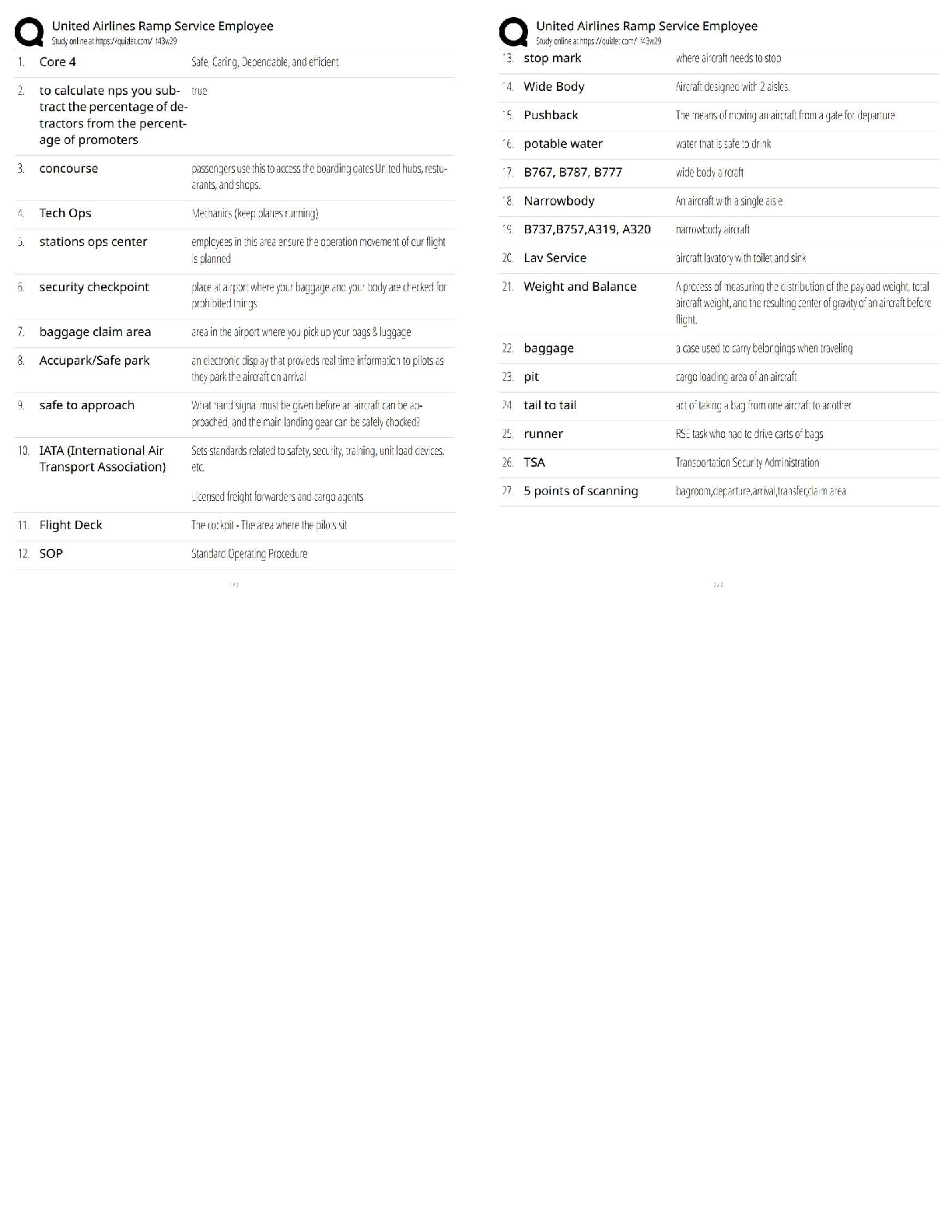
9/5/2019
Homework 2
Question 3.1: Using the same data set (credit_card_data.txt or credit_card_data-headers.txt)
as in Question 2.2, use the ksvm or kknn function to find a good classifier:
(a) using cross
...
ISYE 6501
9/5/2019
Homework 2
Question 3.1: Using the same data set (credit_card_data.txt or credit_card_data-headers.txt)
as in Question 2.2, use the ksvm or kknn function to find a good classifier:
(a) using cross-validation (do this for the k-nearest-neighbors model; SVM is optional);
Answer:
To approach cross-validation for the KNN model, I attempted to leverage the kknn’s built-in
cross-validation function: train.knn. This function uses leave-one-out cross-validation which
means that every data point has a model fit to all other data points. LOOCV is essentially doing
cross-validation X number of times where X is the number of data points. In my approach, I
decided to test 20 values of K (just as in week 1) except this time I introduced a Kmax variable
for robustness of code (easy to change to test more values). I once again scaled the data for a
better fit. The total number of correctly predicted data points, were divided by the total number
of data points to give a percentage of correct points for each K value.
The results indicated that low values of K performed the worst (i.e K=1 is only 81% accurate)
and that K>5 tends to produce fairly similar results with peaks around K=12 and K=15-17 at
85.3% accuracy. It is important to note that despite a decently high predictive value here, our
model quality might not necessarily be high and we would need extraneous data outside of our
train/validation set to confirm.
To approach cross-validation for the SVM model, I simply found the argument parameter cross
to include at the end of my line call for the KSVM function from last week’s homework and set
that equal to 20 to do 20x cross validation of the data. I also found the call: model@cross which
shows the error measured by cross-validation, and hence could use that to determine the
accuracy of this model. Finally I used a for loop with various values of C in order to test the
accuracy of each one (I tested 10 values from 0.000001 to 1000 by magnitudes of 10). As noted
in last week’s homework, larger values of C tend to give better results but reaching a saturation
point around C=0.01 of about 86.2% accuracy.
Code:
KNN
rm(list = ls())
install.packages("kknn")
library(kknn)
data <- read.table("/Users/Vikram/Downloads/credit_card_data.txt", stringsAsFactors = FALSE,
header = FALSE)
head(data)
set.seed(1)
kmax <- 20
model <- train.kknn(V11~.,data,kmax=kmax,scale=TRUE)
accuracy <- rep(0,kmax)
for (k in 1:kmax) {
This study source was downloaded by 100000842525582 from CourseHero.com on 05-13-2022 05:04:36 GMT -05:00
https://www.coursehero.com/file/50101369/GTech-Homework-2/ISYE 6501
9/5/2019
predicted <- as.integer(fitted(model)[[k]][1:nrow(data)] + 0.5)
accuracy[k] <- sum(predicted == data$V11) / nrow(data)
}
accuracy
SVM
library(kernlab)
data <- read.table("/Users/Vikram/Downloads/credit_card_data.txt", stringsAsFactors = FALSE,
header = FALSE)
head(data)
set.seed(1)
acc<-c(0,0,0,0,0,0,0,0,0,0)
C <- c(0.000001,0.00001, 0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000)
for (i in 1:10) {
model <- ksvm(as.matrix(data[,1 :10]),as.factor(data[,11 ]), type = "C-svc", kernel = "vanilladot",
C = C[i], scaled=TRUE, cross=20)
acc[i]<-1-model@cross
}
acc[1:10]
OUTPUT
KNN
[1] 0.8149847 0.8149847 0.8149847 0.8149847 0.8516820 0.8455657 0.8470948
[8] 0.8486239 0.8470948 0.8516820 0.8516820 0.8532110 0.8516820 0.8516820
[15] 0.8532110 0.8532110 0.8532110 0.8516820 0.8501529 0.8501529
SVM
[1] 0.5478693 0.5473485 0.5476326 0.8319602 0.8625000 0.8624527 0.8627841
[8] 0.8621212 0.8623106 0.8623106
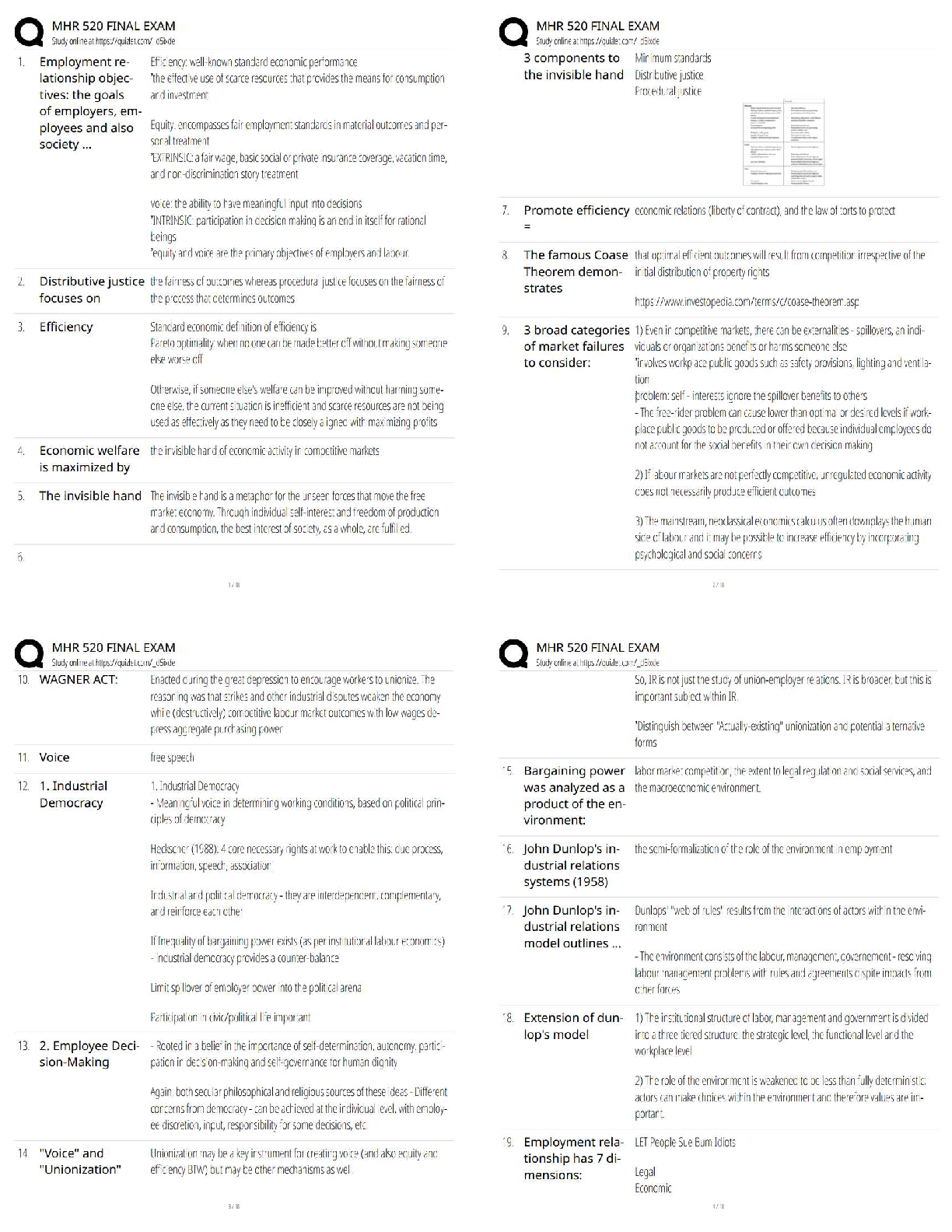
(b) splitting the data into training, validation, and test data sets (pick either KNN or SVM;
the other is optional).
Answer:
I elected to test both methods (KNN and SVM). My methodology was to first split the data into
the three different sets stated in the question: training, validation, and test sets. I chose an
arbitrary split of 70%, 15%, 15% for the data (A near limitless number of different splits could
have been used here that would produce slightly different answers, if I had more time I would
elect to try to write code that would compare all different splits and use recursive analysis to
further optimize cross validation through the use of the optimal split.) Next, I fit all of the models
I have been experimenting with both in this week and last week’s homework assignments to the
training data.This includes 10 SVM models (0.000001 to 1000 by magnitudes of 10) ad 20 KNN
models (K=1 to K=20) for a total of 30 models. Then, I evaluated these models on the validation
This study source was downloaded by 100000842525582 from CourseHero.com on 05-13-2022 05:04:36 GMT -05:00
https://www.coursehero.com/file/50101369/GTech-Homework-2/ISYE 6501
9/5/2019
data. C=0.01 was the best SVM model and K=17 was the best KNN model.
It should be noted that several values were close and hence the selection of best is minute and
slightly arbitrary, the general principle is that K>5 and C>0.01 are the best models. The final
step of the code is a conditional evaluation to check and report whether the SVM or the KNN
model is better overall. This is included so that this generalized code could be applied to other
broader sets where there might be a different solution. For this assignment the SVM 0.01
model was best with a 0.867 test accuracy. It should be noted that several KNN models
actually outperformed this SVM model on the test set, but that they fell short in validation. Using
the test data to validate instead of the validation data would defeat the entire purpose of this
exercise and introduce selection bias.
Code:
rm(list = ls())
library(kernlab)
install.packages("kknn")
library(kknn)
data <- read.table("/Users/Vikram/Downloads/credit_card_data.txt", stringsAsFactors = FALSE,
header = FALSE)
head(data)
set.seed(1)
filter = sample(nrow(data), size = floor(nrow(data) * 0.7))
train_set= data[filter,]
non_train = data[-filter, ]
filter_val = sample(nrow(non_train), size = floor(nrow(non_train)/2))
val_set = non_train[filter_val,]
test_set = non_train[-filter_val, ]
acc <- rep(0,30)
C <- c(0.000001,0.00001, 0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000)
for (i in 1:10)
{model <- ksvm(as.matrix(train_set[,1 :10]),as.factor(train_set[,11 ]), type = "C-svc", kernel =
"vanilladot", C
= C[i], scaled=TRUE)
pred <- predict(model,val_set[,1:10])
acc[i] = sum(pred == val_set$V11) / nrow(val_set)
}
acc[1:10]
cat("The Best SVM Model is ", C[which.max(acc[1:10])], " with ", max(acc[1:10]))
model <- ksvm(as.matrix(train_set[,1 :10]),as.factor(train_set[,11 ]), type = "C-svc", kernel
[Show More]