19.9
a.) Using the .01 level of significance, test the null hypothesis that in the
underlying population, crimes are equally likely to be committed on any day
of the week.
Response:
H0=Psun=Pmon=Ptues=Pwed=Pthurs=Pf
...
19.9
a.) Using the .01 level of significance, test the null hypothesis that in the
underlying population, crimes are equally likely to be committed on any day
of the week.
Response:
H0=Psun=Pmon=Ptues=Pwed=Pthurs=Pfri=Psat=
1
7
H1
: H0
isfalse
Decision Rule: Reject H0 at the 0.01 level of significance is x
2
≥16.81
Calculations:
totalsample¿ ¿
f e=( expected proportion) ¿
Frequen
cy
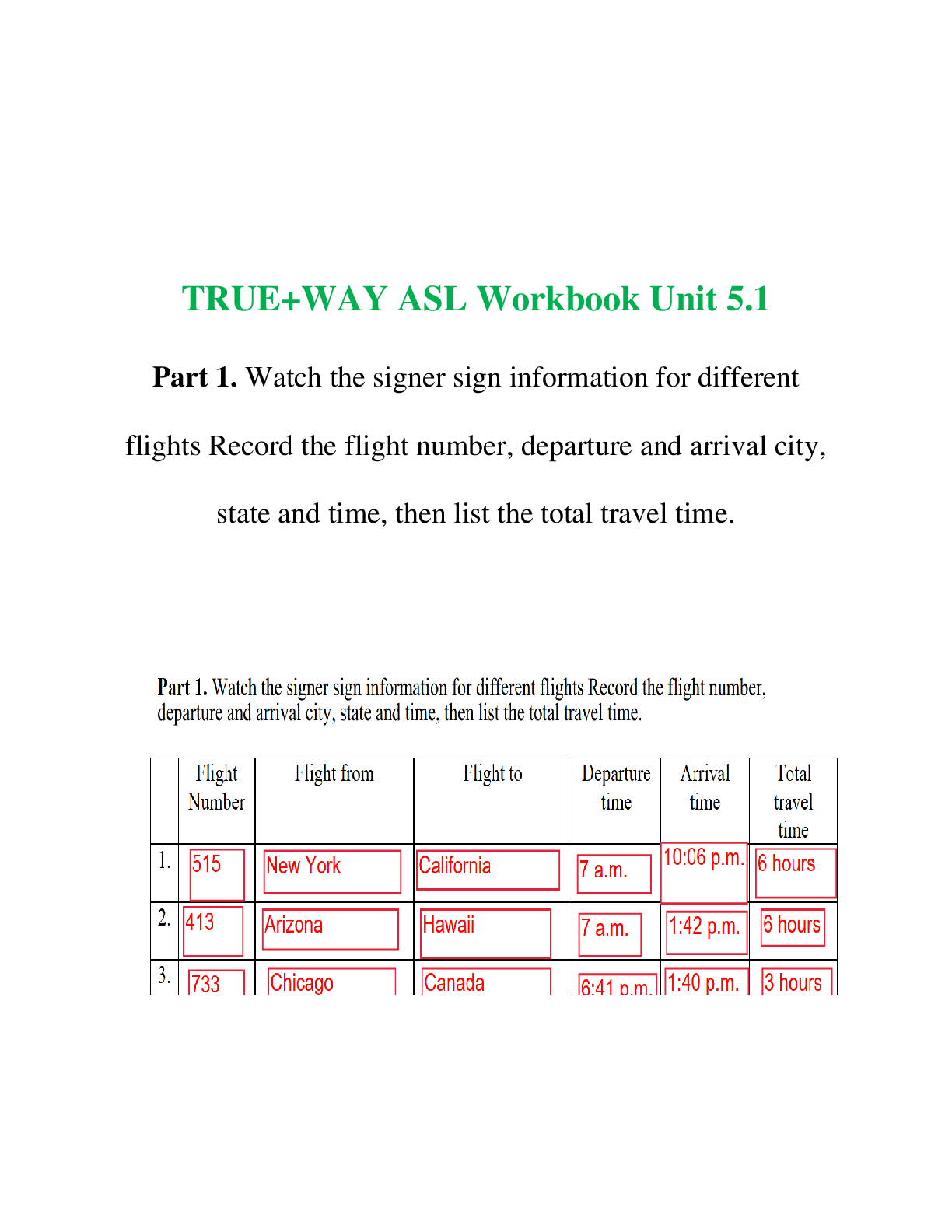
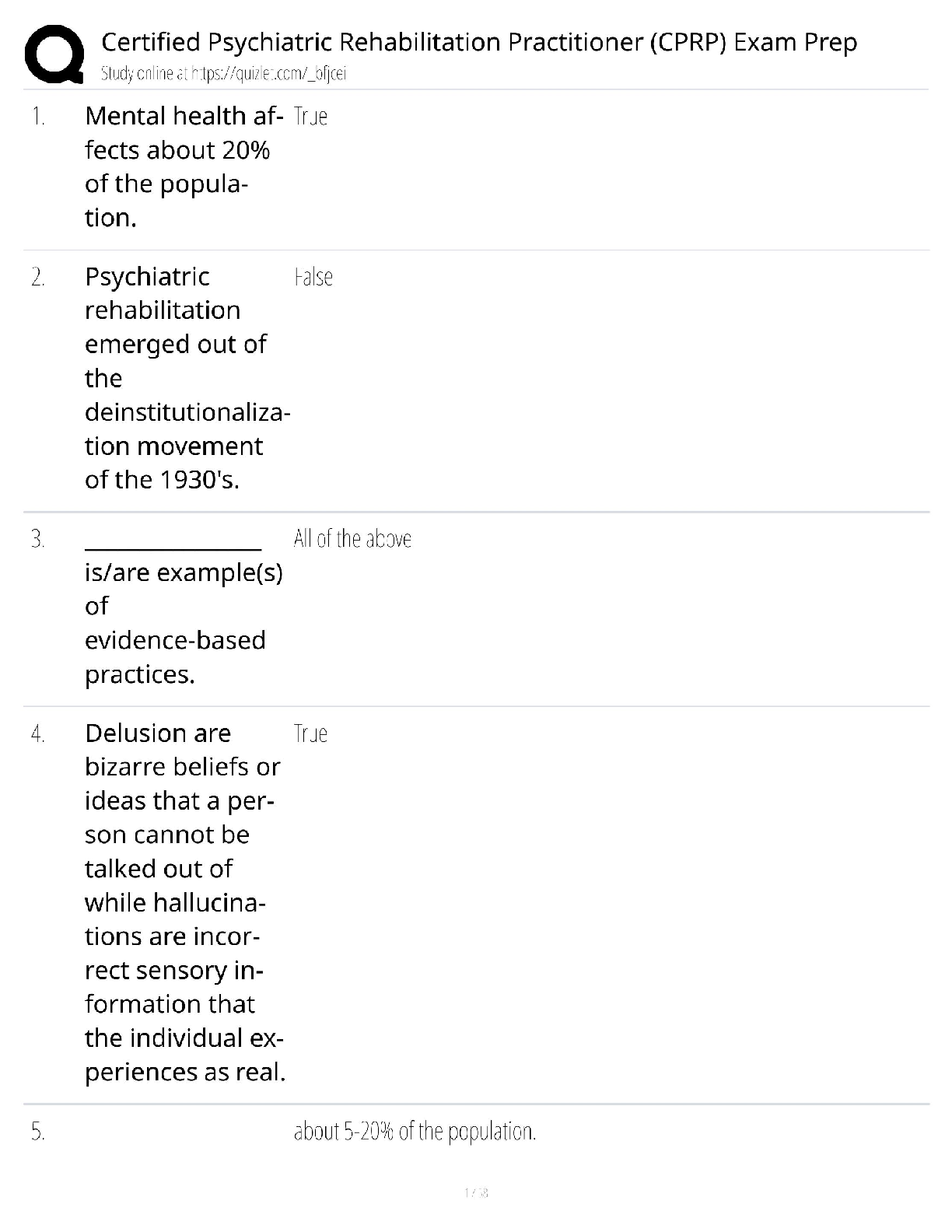
Mon Tues Wed Thurs Fri Sat Sun Total
f
o 17 21 22 18 23 24 15 140
f
e 20 20 20 20 20 20 20 140
Null hypothesis:
x
2=∑
(f o−f e
)2
f
e
¿ {
(17−20)
2
20
+
(21−20)
2
20
+
(22−20)
2
20
+
(18−20)
2
20
+
(23−20)
2
20
+
(24−20)
2
20
+
(15−20)
2
20 }
=
9
20
+
1
20
+
4
20
+
4
20
+
9
20
+
16
20
+
25
20
=
68
20
= 3.4
Return the null hypothesis at 0.01 level because the observed x
2
of 3.4 is
smaller than the critical x
2
of 16.81. Crimes are likely to be committed on
any day of the week.
b.) Specify the approximate p -value for this test result.
At 1% level significance, we return the null hypothesis H0 indicates the pvalue is greater than 0.01, that is, p>0.01. In the x
2
table values we
observe the value 12.6 at 0.05 level and degrees of freedom = 6. We can
retain the null hypothesis at 5% level too. Therefore p>0.05.
c.) How might this result be reported in literature?
There is evidence that the crimes are equally likely to take place on any day
of the week [ x
2
(6,n=200)=3.4, p>0.05] .
We are unable to calculate ∅c
2
, since
non-significant x
2
at 0.01 level. The parenthetical statement indicates that
a x
2
based on 6 degrees of freedom and a sample size of 140 was found to
equal 3.4. The test result has an approximate p-value greater than 0.05,
because the null hypothesis was retained.
19.10
a.) Test the null hypothesis that this coin is unbiased, that is, that heads and tails are
equally likely to appear in the long run.
Null hypothesis
H0
: Pheads=Ptails=
1
248
Decision rule: Reject H0 at the 0.05 level of significance; if x2 ≥3.84 ,
given that the degrees of freedom equals to
=c-1
=2-1
=1
Calculations:
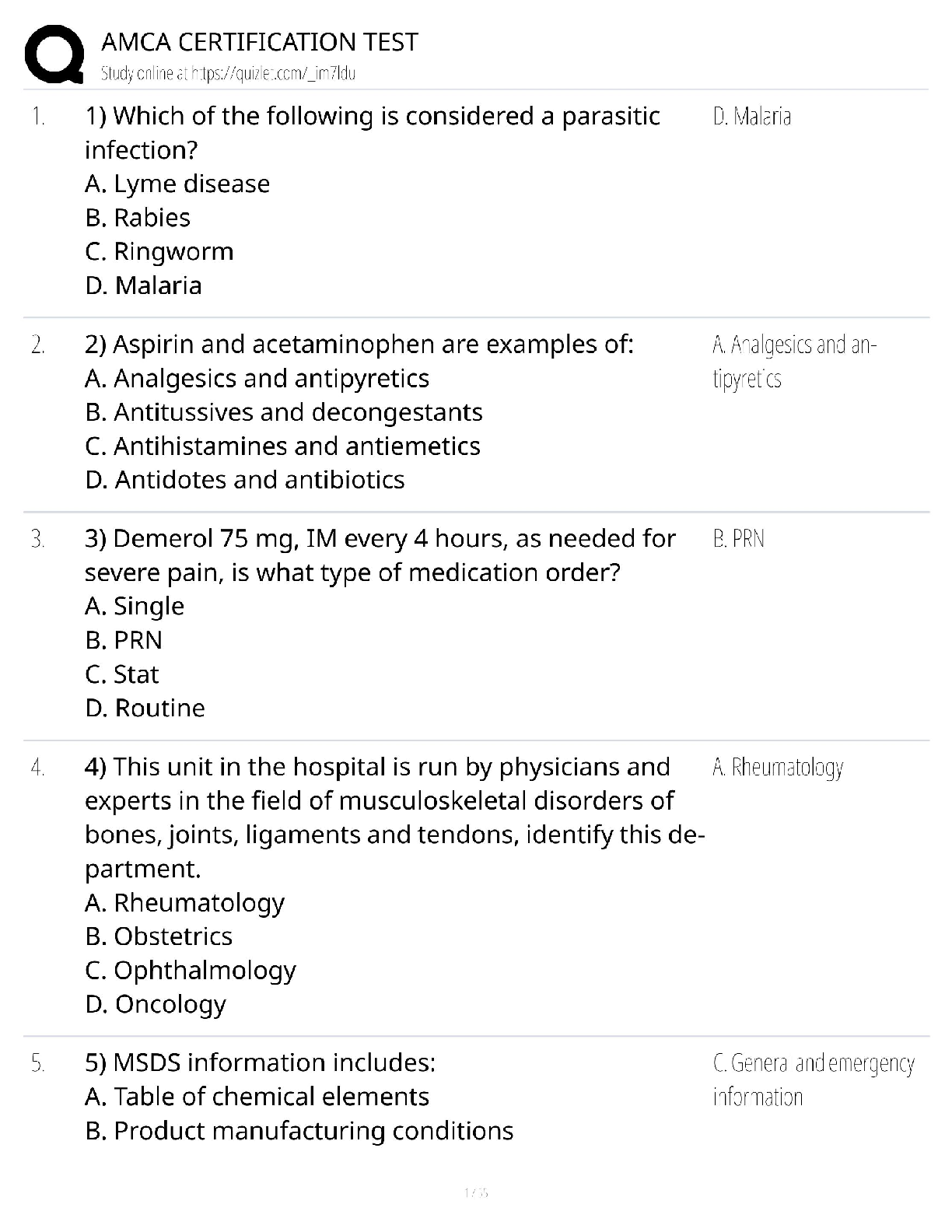
Frequency Heads Tails Total
f
o 30 20 50
f
e 25 25 50
Null hypothesis:
x
2=∑
(f o−f e
)2
f
e
¿ {
(30−25)
2
25
+
(20−25)
2
25 }
=
25
25
+
25
25
= 1+1
= 2
Retain because x
2
of 2 is less than critical x
2
of 3.84.
b.) Specify the approximate p-value for this test result.
p-value is the smallest level of significance that would lead to the rejection
of H0 . Acceptance of it would lead to a greater p-value than significance
level. At the 5% level, we retain H0 implies that the p-value is greater than
a = 0.05.
19.13
a.) Using the .05 level of significance test the null hypothesis that survival
rates are independent of the passengers’ accommodations (cabin or
steerage).
H0 : type of accommodations and survival rates are independent
H1
: H0
isfalse
Decision Rule: Reject the null hypothesis at 0.05 level of significance, if
x
2
≥3.84 , given that the degrees of freedom.
=(c-1)(r-1)
=(2-1)(2-1)
=1
Calculations:
f e=
( columntotal)(rowtotal)
grandtotal
f e
( cabin,survived)=
(579)(485)
1291 =
280815
1291 =217.52
f e
(steerage ,survived)=
(712) (485)
1291 =
345320
1291 =276.48
f e
( cabin, not survived)=
(579)(806)
1291 =
466674
1291 =361.48
f e
(steerage ,notsurvived)=
(712)(806)
1291 =
573872
1291 =444.52
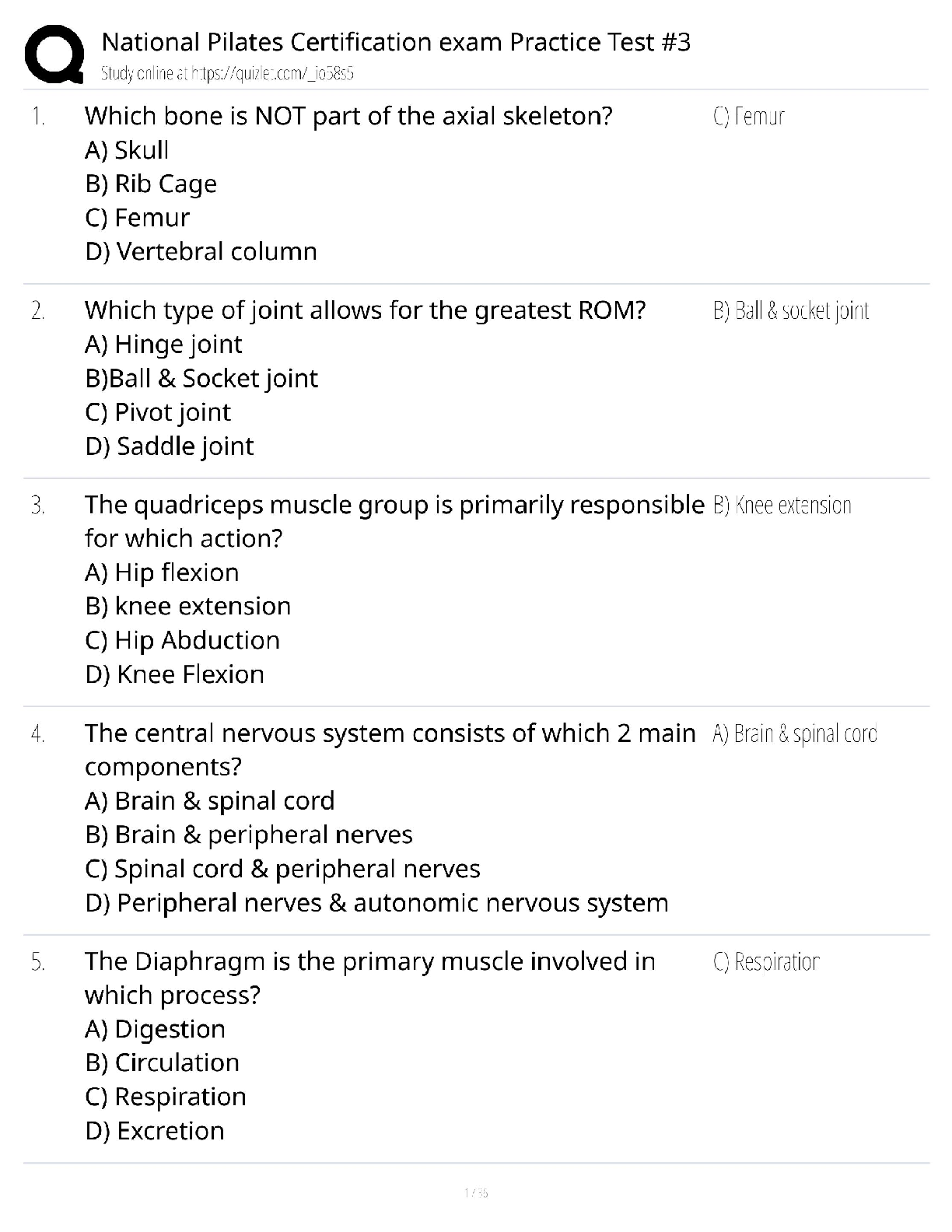
Survived/Accomoda
tion
Cabin Steerage Total
f
o 299 186
485
Yes
f
e
217.52 276.48
f
o
No
f
e
280
361.48
526
444.52
806
Total 579 712 1291
x
2=
(299−217.52)
2
217.52
+
(186−267.48)
2
267.48
+
(280−361.48)
2
361.48
+
(526−444.52)
2
444.52
¿
6638.99
217.52
+
6638.99
267.48
+
6638.99
361.48
+
6638.99
444.52
¿30.52+24.82+18.37+14.94
¿88.65
x
2
of 88.65 is much larger than critical x
2
of 3.84 so the null hypothesis
should be rejected
There is a connection between the type of accommodation in the titanic-ship
and the survival rate
b.)Assuming a significant x
2
, estimates the strength of the relationship.
∅c
2=
88.65
1291(2−1)
=
88.65
1291
=0.07
The strength of the relationship is medium
c.) To more fully appreciate the importance of this relationship, calculate
an odds ratio to determine how much more likely a cabin passenger is
to have survived than a steerage passenger.
[Show More]
.png)