University of Pennsylvania MATH MISC sixthsense24

Document Content and Description Below

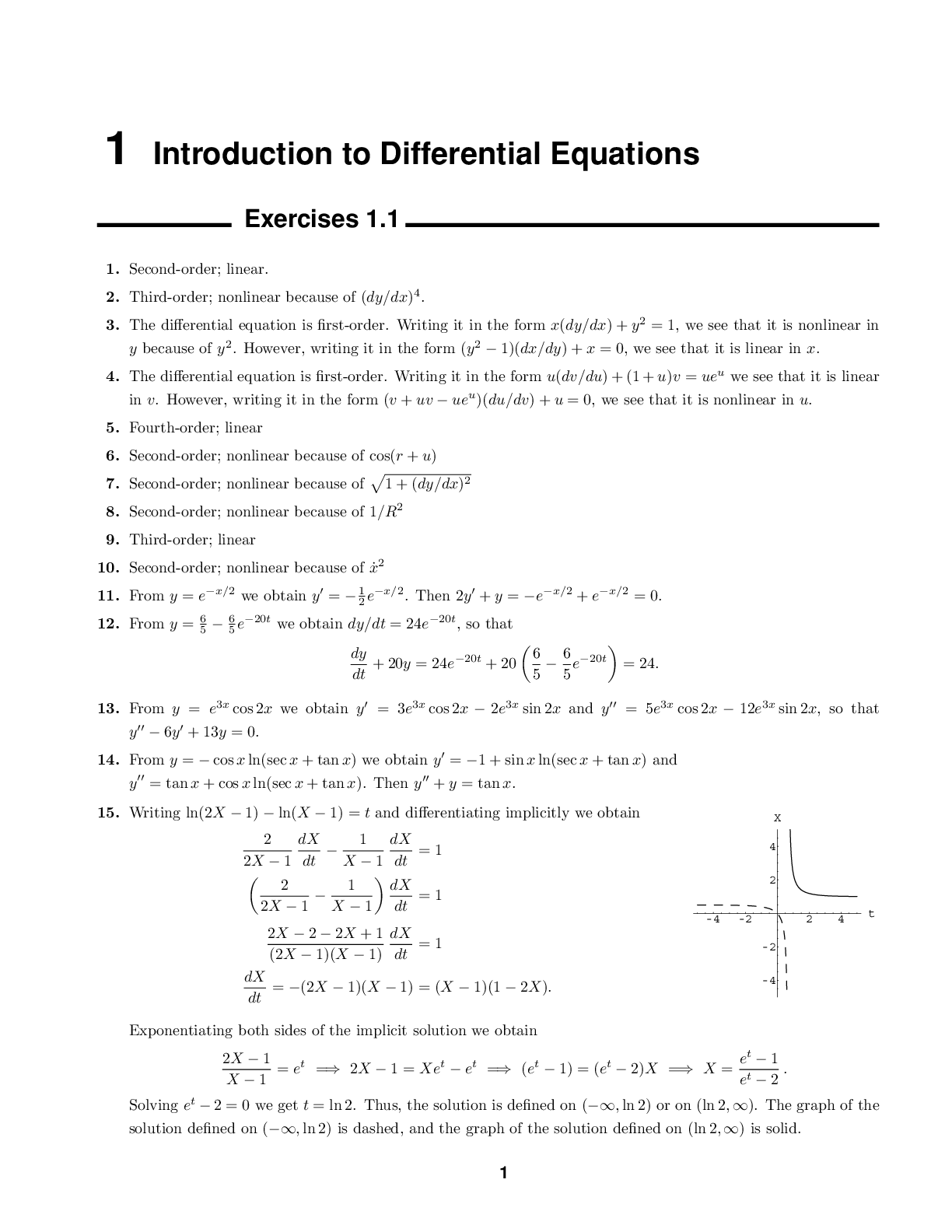
1 Introduction to Differential Equations Exercises 1.1 1. Second-order; linear. 2. Third-order; nonlinear because of (dy/dx)4. 3. The differential equation is first-order. Writing it in the form x... (dy/dx) + y2 = 1, we see that it is nonlinear in y because of y2. However, writing it in the form (y2 − 1)(dx/dy) + x = 0, we see that it is linear in x. 4. The differential equation is first-order. Writing it in the form u(dv/du) + (1 + u)v = ueu we see that it is linear in v. However, writing it in the form (v + uv − ueu)(du/dv) + u = 0, we see that it is nonlinear in u. 5. Fourth-order; linear 6. Second-order; nonlinear because of cos(r + u) 7. Second-order; nonlinear because of !1+(dy/dx)2 8. Second-order; nonlinear because of 1/R2 9. Third-order; linear 10. Second-order; nonlinear because of ˙x2 11. From y = e−x/2 we obtain y" = −1 2 e−x/2. Then 2y" + y = −e−x/2 + e−x/2 = 0. 12. From y = 6 5 − 6 5 e−20t we obtain dy/dt = 24e−20t , so that dy dt + 20y = 24e−20t + 20 "6 5 − 6 5 e−20t # = 24. 13. From y = e3x cos 2x we obtain y" = 3e3x cos 2x − 2e3x sin 2x and y"" = 5e3x cos 2x − 12e3x sin 2x, so that y"" − 6y" + 13y = 0. 14. From y = − cos x ln(sec x + tan x) we obtain y" = −1 + sin x ln(sec x + tan x) and y"" = tan x + cos x ln(sec x + tan x). Then y"" + y = tan x. 15. Writing ln(2X − 1) − ln(X − 1) = t and differentiating implicitly we obtain 2 2X − 1 dX dt − 1 X − 1 dX dt = 1 " 2 2X − 1 − 1 X − 1 # dX dt = 1 2X − 2 − 2X + 1 (2X − 1)(X − 1) dX dt = 1 dX dt = −(2X − 1)(X − 1) = (X − 1)(1 − 2X). Exponentiating both sides of the implicit solution we obtain 2X − 1 X − 1 = et =⇒ 2X − 1 = Xet − et =⇒ (et − 1) = (et − 2)X =⇒ X = et − 1 et − 2 . Solving et − 2 = 0 we get t = ln 2. Thus, the solution is defined on (−∞, ln 2) or on (ln 2,∞). The graph of the solution defined on (−∞, ln 2) is dashed, and the graph of the solution defined on (ln 2,∞) is solid. 1 -4 -2 2 4 x -4 -2 2 4 y Exercises 1.1 16. Implicitly differentiating the solution we obtain −2x2 dy dx − 4xy + 2y dy dx =0 =⇒ −x2 dy − 2xy dx + y dy = 0 =⇒ 2xy dx + (x2 − y)dy = 0. Using the quadratic formula to solve y2 − 2x2y − 1 = 0 for y, we get y = $ 2x2 ± √4x4 + 4 % /2 = x2 ± √x4 + 1 . Thus, two explicit solutions are y1 = x2 + √x4 + 1 and y2 = x2 − √x4 + 1 . Both solutions are defined on (−∞,∞). The graph of y1(x) is solid and the graph of y2 is dashed. 17. Differentiating P = c1et / (1 + c1et ) we obtain dP dt = (1 + c1et ) c1et − c1et · c1et (1 + c1et) 2 = c1et 1 + c1et [(1 + c1et ) − c1et ] 1 + c1et = P(1 − P). 18. Differentiating y = e−x2 & x 0 et2 dt + c1e−x2 we obtain y" = e−x2 ex2 − 2xe−x2 & x 0 et2 dt − 2c1xe−x2 = 1 − 2xe−x2 & x 0 et2 dt − 2c1xe−x2 . Substituting into the differential equation, we have y" + 2xy = 1 − 2xe−x2 & x 0 et2 dt − 2c1xe−x2 + 2xe−x2 & x 0 et2 dt + 2c1xe−x2 = 1. 19. From y = c1e2x + c2xe2x we obtain dy dx = (2c1 + c2)e2x + 2c2xe2x and d2y dx2 = (4c1 + 4c2)e2x + 4c2xe2x, so that d2y dx2 − 4 dy dx + 4y = (4c1 + 4c2 − 8c1 − 4c2 + 4c1)e2x + (4c2 − 8c2 + 4c2)xe2x = 0. 20. From y = c1x−1 + c2x + c3x ln x + 4x2 we obtain dy dx = −c1x−2 + c2 + c3 + c3 ln x + 8x, d2y dx2 = 2c1x−3 + c3x−1 + 8, and d3y dx3 = −6c1x−4 − c3x−2, so that x3 d3y dx3 + 2x2 d2y dx2 − x dy dx + y = (−6c1 + 4c1 + c1 + c1)x−1 + (−c3 + 2c3 − c2 − c3 + c2)x + (−c3 + c3)x ln x + (16 − 8 + 4)x2 = 12x2. 21. From y = ' −x2, x< 0 x2, x ≥ 0 we obtain y" = ' −2x, x < 0 2x, x ≥ 0 so that xy" − 2y = 0. 2 Exercises 1.1 22. The function y(x) is not continuous at x = 0 since lim x→0− y(x) = 5 and limx→0+ y(x) = −5. Thus, y" (x) does not exist at x = 0. 23. From x = e−2t + 3e6t and y = −e−2t + 5e6t we obtain dx dt = −2e−2t + 18e6t and dy dt = 2e−2t + 30e6t . Then x + 3y = (e−2t + 3e6t ) + 3(−e−2t + 5e6t ) = −2e−2t + 18e6t = dx dt and 5x + 3y = 5(e−2t + 3e6t ) + 3(−e−2t + 5e6t ) = 2e−2t + 30e6t = dy dt . 24. From x = cos 2t + sin 2t + 1 5 et and y = − cos 2t − sin 2t − 1 5 et we obtain dx dt = −2 sin 2t + 2 cos 2t + 1 5 et and dy dt = 2 sin 2t − 2 cos 2t − 1 5 et and d2x dt2 = −4 cos 2t − 4 sin 2t + 1 5 et and d2y dt2 = 4 cos 2t + 4 sin 2t − 1 5 et . Then 4y + et = 4(− cos 2t − sin 2t − 1 5 et ) + et = −4 cos 2t − 4 sin 2t + 1 5 et = d2x dt2 and 4x − et = 4(cos 2t + sin 2t + 1 5 et ) − et = 4 cos 2t + 4 sin 2t − 1 5 et = d2y dt2 . 25. An interval on which tan 5t is continuous is −π/2 < 5t < π/2, so 5 tan 5t will be a solution on (−π/10, π/10). 26. For (1 − sin t)−1/2 to be continuous we must have 1 − sin t > 0 or sin t < 1. Thus, (1 − sin t)−1/2 will be a solution on (π/2, 5π/2). 27. (y" )2 + 1 = 0 has no real solution. 28. The only solution of (y" )2 + y2 = 0 is y = 0, since if y &= 0, y2 > 0 and (y" )2 + y2 ≥ y2 > 0. 29. The first derivative of f(t) = et is et . The first derivative of f(t) = ekt is kekt. The differential equations are y" = y and y" = ky, respectively. 30. Any function of the form y = cet or y = ce−t is its own second derivative. The corresponding differential equation is y"" − y = 0. Functions of the form y = c sin t or y = c cost have second derivatives that are the negatives of themselves. The differential equation is y"" + y = 0. 31. Since the nth derivative of φ(x) must exist if φ(x) is a solution of the nth order differential equation, all lowerorder derivatives of φ(x) must exist and be continuous. [Recall that a differentiable function is continuous.] 32. Solving the system c1y1(0) + c2y2(0) = 2 c1y" 1(0) + c2y" 2(0) = 0 [Show More]

Last updated: 2 years ago

Preview 1 out of 841 pages