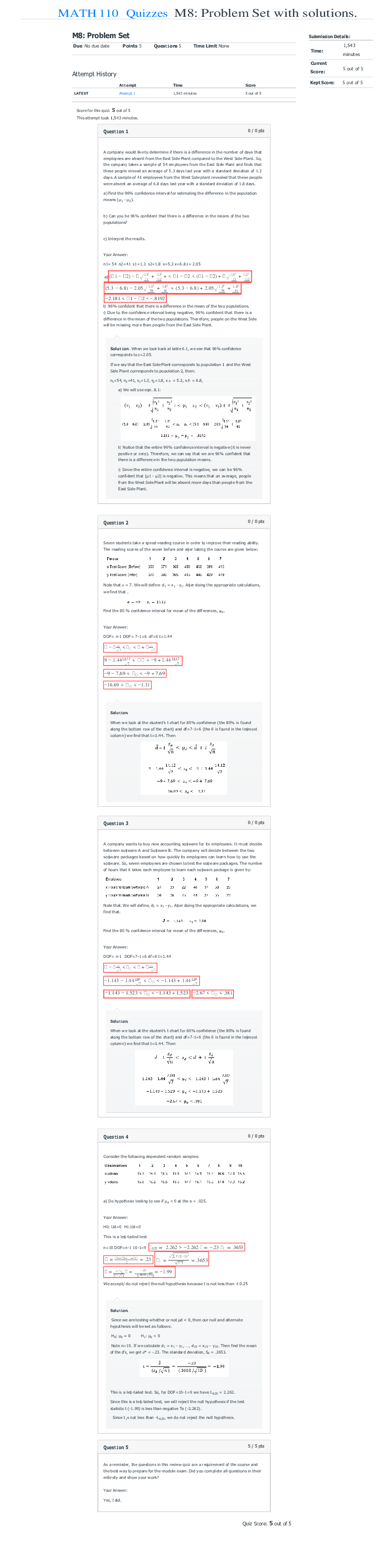
A company would like to determine if there is a difference in the number of days that
employees are absent from the East Side Plant compared to the West Side Plant. So,
the company takes a sample of 54 employees from t
...
A company would like to determine if there is a difference in the number of days that
employees are absent from the East Side Plant compared to the West Side Plant. So,
the company takes a sample of 54 employees from the East Side Plant and finds that
these people missed an average of 5.3 days last year with a standard deviation of 1.3
days. A sample of 41 employees from the West Side plant revealed that these people
were absent an average of 6.8 days last year with a standard deviation of 1.8 days.
a) Find the 96% confidence interval for estimating the difference in the population
means (µ1 - µ2).
b) Can you be 96% confident that there is a difference in the means of the two
populations?
c) Interpret the results.
Your Answer:
n1= 54 n2=41 s1=1.3 s2=1.8 x=5.3 x=6.8 z= 2.05
b) 96% confident that there is a difference in the mean of the two populations.
c) Due to the confidence interval being negative, 96% confident that there is a
difference in the mean of the two populations. Therefore, people on the West Side
will be missing more than people from the East Side Plant.
Solution. When we look back at table 6.1, we see that 96% confidence
corresponds to z=2.05.
If we say that the East Side Plant corresponds to population 1 and the West
Side Plant corresponds to population 2, then:
n1=54, n2=41, s1=1.3, s2=1.8, xぁ = 5.3, xあ = 6.8,
a) We will use eqn. 8.1:
b) Notice that the entire 96% confidence interval is negative (it is never
positive or zero). Therefore, we can say that we are 96% confident that
there is a difference in the two population means.
c) Since the entire confidence interval is negative, we can be 96%
confident that (µ1 - µ2) is negative. This means that on average, people
from the West Side Plant will be absent more days than people from the
East Side Plant.
[Show More]


.png)