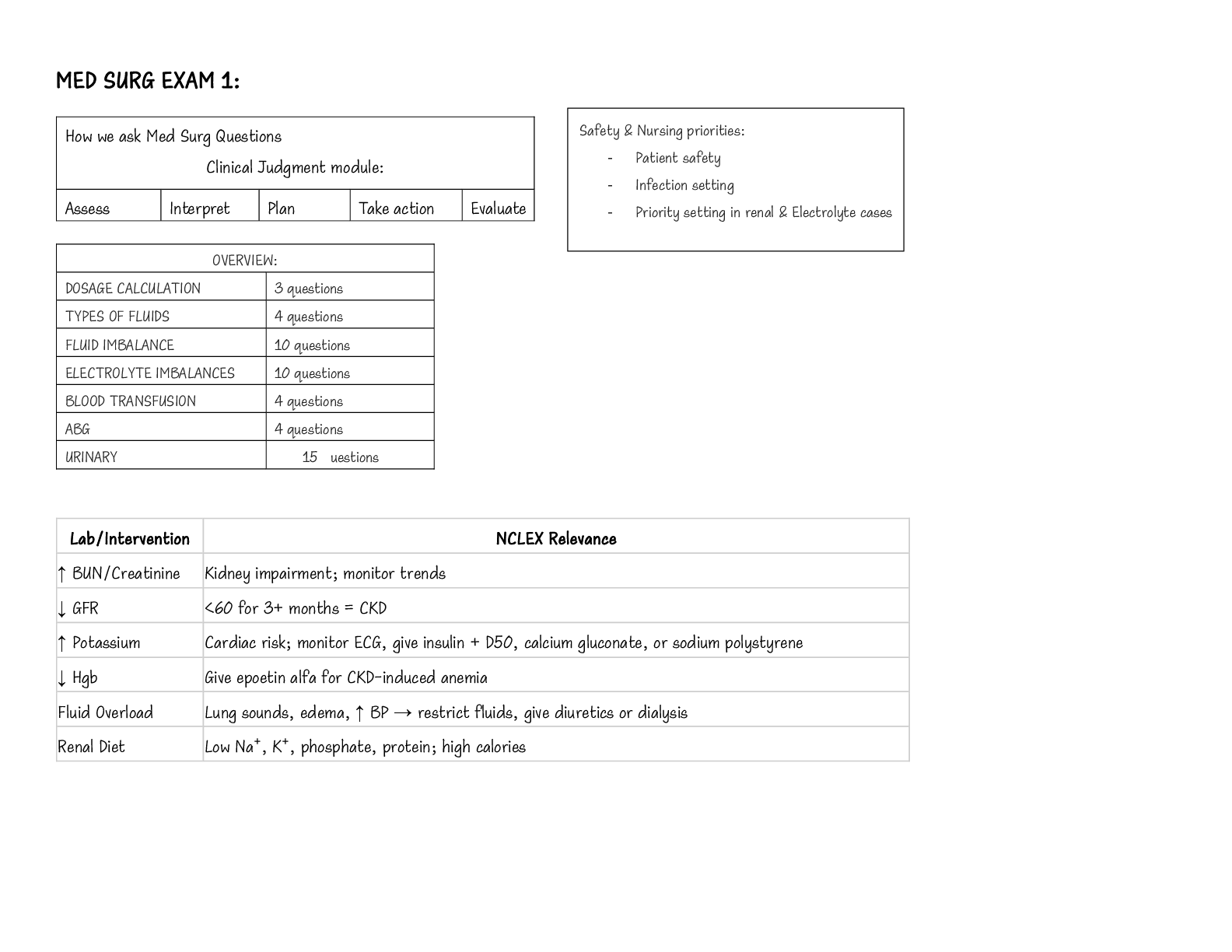
STAT 200 Week 6 Homework Problems
9.1.2
Many high school students take the AP tests in different subject areas. In 2007, of the 144,796 students
who took the biology exam 84,199 of them were female. In that same year,
...
STAT 200 Week 6 Homework Problems
9.1.2
Many high school students take the AP tests in different subject areas. In 2007, of the 144,796 students
who took the biology exam 84,199 of them were female. In that same year, of the 211,693 students who
took the calculus AB exam 102,598 of them were female ("AP exam scores," 2013). Estimate the
difference in the proportion of female students taking the biology exam and female students taking the
calculus AB exam using a 90% confidence level.
Difference in the proportion of female students taking the Biology exam and female students taking the
calculus AB exam using a 90% CI:
Here, we have it that:
n1 = 144,796 n2 = 211,693
x1 = 84,199 x2 = 102,598
C = 1 - α = 1 - 0.9 = 0.1
For this problem, we are to estimate a 90% confidence interval on the difference in proportion of female
students taking the biology and calculus AB exam.
This difference is given by: p1 – p2
Where;
x1 = number of female students taking the biology exam
x2 = number of female students taking the calculus AB exam
p1 = proportion of female students taking the biology exam
p2 = proportion of female students taking the calculus AB exam
x1 = 84,199
n1 - x1 = 144,796 - 84,199 = 60597
x2 = 102,598
n2 - x2 = 211,693 - 102,598 = 109095
are all greater than or equal to 5, we assume both sampling distributions of �̂1 and �̂2 can be
approximated with a normal distribution.
�̂1 = x1/n1 = 84199/144796 = 0.5815, �̂2 = x2/n2 = 102598/211693 = 0.4847
�̂1 = 1 − �̂1 = 1 − 84199/144796 = 0.4185, �̂2 = 1 − �̂2 = 1 − 102598/211693 = 0.5153
To calculate the z-value in excel, =NORM.S.INV (0.95) = 1.645, and use this to find the margin error:
E = 1.645*(sqrt (((0.5815*0.4185)/144796) + ((0.4847*0.5153)/211693))) = 0.0028
Then use it to compute the confidence interval on p1 - p2:
(�1 − �̂2) − � < (�1 − �2) < (�̂1 − �̂2) + �
(0.5815 − 0.4847) − 0.0028 < (�1 − �2) < (0.5815 − 0.4847) + 0.0028
�. �??� < (?� − ?�) < �. �??�
Statistical Interpretation: There is a 90% chance that �. �??� < (?� − ?�) < �. �??� contains the true
difference in proportions.
Conclusion: The proportion of female students taking the biology exam is anywhere from 9.41% to 9.96%
higher than the proportion of female students taking the calculus AB exam.
9.1.5
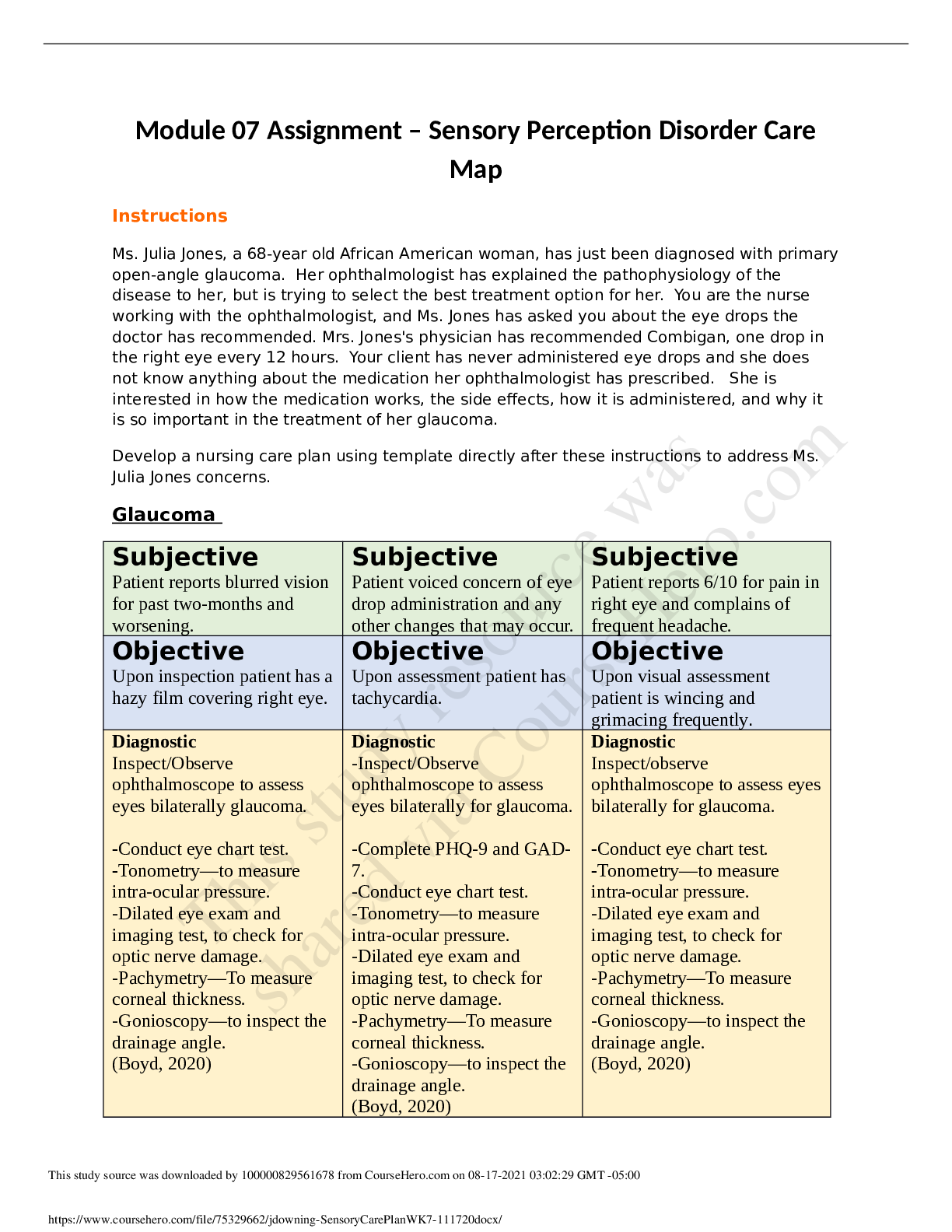
Are there more children diagnosed with Autism Spectrum Disorder (ASD) in states that have larger urban
areas over states that are mostly rural? In the state of Pennsylvania, a fairly urban state, there are 245
eight year olds diagnosed with ASD out of 18,440 eight year olds evaluated. In the state of Utah, a fairly
rural state, there are 45 eight year olds diagnosed with ASD out of 2,123 eight year olds evaluated
("Autism and developmental," 2008). Is there enough evidence to show that the proportion of children
diagnosed with ASD in Pennsylvania is more than the proportion in Utah? Test at the 1% level.
Testing at 1% level of significance:
Here, we have it that;
n1 = 18,440 n2 = 2,123
x1 = 245 x2 = 45
α = 0.01
For this problem, we are testing whether the proportion of children diagnosed with ADS in Pennsylvania
is more than that of Utah.
Where;
x1 = number of children diagnosed with Autism Spectrum Disorder (ASD) in Pennsylvania
x2 = number of children diagnosed with ASD in Utah
p1 = proportion of children diagnosed with ASD in Pennsylvania
p2 = proportion of children diagnosed with ASD in Utah
The hypothesis will be:
H0 : p1 = p2 Vs. H1 : p1 > p2
x1 = 245 n1 - x1 = 18440 -245 = 18195
x2 = 45 n2 - x2 = 2123 - 45 = 2078
are all greater than or equal to 5, we assume both sampling distributions of �̂1 and �̂2 can be
approximated with a normal distribution.
�̂1 = �1/�1 = 245/18144 = 0.0133, �̂2 = �2/�2 = 45/2123 = 0.0212
�̂1 = 1 − �̂1 = 1 − 245/18144 = 0.9867, �̂2 = 1 − �̂2 = 1 − 45/2123 = 0.9788
Then compute the pooled proportions,
�̅ = (245 + 45) / (18144 + 2123) = 0.0141
and �̅ = 1 – 0.0141 = 0.9859
the test statistic z = -2.927
Conclusion
Since the p-value is greater than the level of significance (i.e. [p-value = 0.9983] > [α = 0.01]), we fail to
reject ?�.
This is not enough evidence to show that the proportion of children diagnosed with ASD in Pennsylvania
is more than the proportion of children diagnosed with ASD in Utah.
9.2.3
All Fresh Seafood is a wholesale fish company based on the east coast of the U.S. Catalina Offshore
Products is a wholesale fish company based on the west coast of the U.S. Table #9.2.5 contains prices
from both companies for specific fish types ("Seafood online," 2013) ("Buy sushi grade," 2013). Do the
data provide enough evidence to show that a west coast fish wholesaler is more expensive than an east
coast wholesaler? Test at the 5% level.
Table #9.2.5: Wholesale Prices of Fish in Dollars
Fish
All Fresh
Seafood
Prices
Catalina
Offshore
Products Prices
Cod 19.99 17.99
Tilapi 6.00 13.99
Farmed Salmon 19.99 22.99
Organic Salmon 24.99 24.99
Grouper Fillet 29.99 19.99
Tuna 28.99 31.99
Swordfish 23.99 23.99
Sea Bass 32.99 23.99
Striped Bass 29.99 14.99
Testing at 5% level of significance:
We have that;
n = 9
α = 0.05
For this problem, we are testing whether a west coast fish wholesaler is more expensive than an east
coast wholesaler.
Where;
x1 = wholesale prices from west coast fishery
x2 = wholesale prices from east coast fishery
μ1 = mean wholesale prices from west coast fishery
μ2 = mean wholesale prices from east coast fishery
the hypothesis will be;
H0: �1 = �2 Vs. H1: �1 > �2 at � = 0.05
Thus �̅= $2.446 and s� = $7.399, where �̅ is the sum of the difference between x1 and x2 divided by n
and sd is the standard deviation of the difference.
Thus t = (2.446 – 0) / (7.399/ sqrt(9)) = 0.9915
We can get the p- value in excel by: =1 - T.DIST(
[Show More]



















.png)