Mathematics > CHEAT SHEET > AMS 301 Cheat Sheet – Midterm 1 (Sept. 29th) | Download for quality grades | (All)
AMS 301 Cheat Sheet – Midterm 1 (Sept. 29th) | Download for quality grades |
Document Content and Description Below
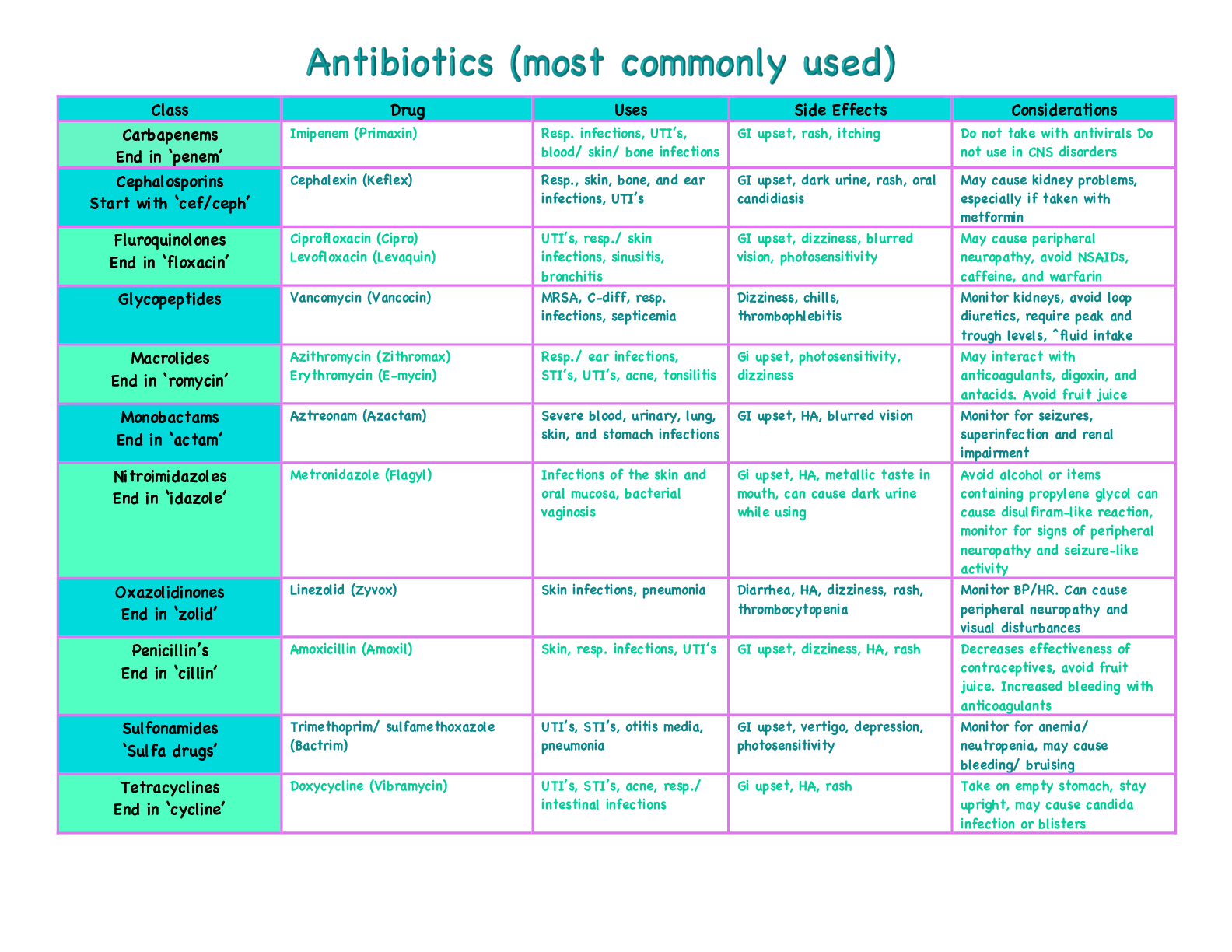
Terminology: 1. Connected Graph: There is a path (NOT edge) between every pair of vertices. 2. Isomorphism: There exists one-to-one correspondence in two isomorphic graphs. 3. Sub-graph: Formed by ... a subset of vertices and edges. 4. Complete Graph: Each vertex is adjacent to all other vertices. (Notation: Kn) 5. Graph Components: A component H of a graph G is a connected sub-graph of G. Besides, there is no path between any vertex in H and any vertex not in H. 6. Bipartite Graph: Every circuit in G has even length. Set of all vertices V can be divided into V1 and V2 such that every edge joins a vertex in V1 with vertex in V2. 7. Planar Graph: A graph can be drawn on a plane without edge crossing. 8. Euler Trail: A path with no repeated edges and contains all the edges in the graph. 9. Euler Cycle: a cycle that contains all edges in a graph. 10. Multi-graph: multiple edges connecting the same pair of vertices. 11. Hamilton Circuit: A circuit that visits each vertex exactly once. Theorem: 1. Edge Counting: In any graph, the sum of all vertices degree = 2 * (# of edges) 2. Kuratowski’s Theorem: A graph is planar if and only if it does not contain a sub-graph that is K5 or K3,3. 3. Euler’s Theorem 1: If G is a connected planar graph, then any plane depiction of G must have r = e – v + 2 regions. (e = # of edges, v = # of vertices) 4. Euler’s Theorem 2: A multi-graph has an Euler cycle if and only if it is connected and has all vertices of even degree. 5. Edge Vertices Rule: If G is a c [Show More]
Last updated: 2 years ago
Preview 1 out of 2 pages

Buy this document to get the full access instantly
Instant Download Access after purchase
Buy NowInstant download
We Accept:

Reviews( 0 )
$2.00
Can't find what you want? Try our AI powered Search
Document information
Connected school, study & course
About the document
Uploaded On
Feb 12, 2023
Number of pages
2
Written in
All
Additional information
This document has been written for:
Uploaded
Feb 12, 2023
Downloads
0
Views
144

.png)