
AMT2 KMM1 TASK 1.pdf AMT2 SERVICE LINE DEVELOPMENT WESTERN GOVERNORS UNIVERSITY AMT2 K
$ 10

Safely Preparing and Giving Drugs Workman & LaCharity:
$ 7
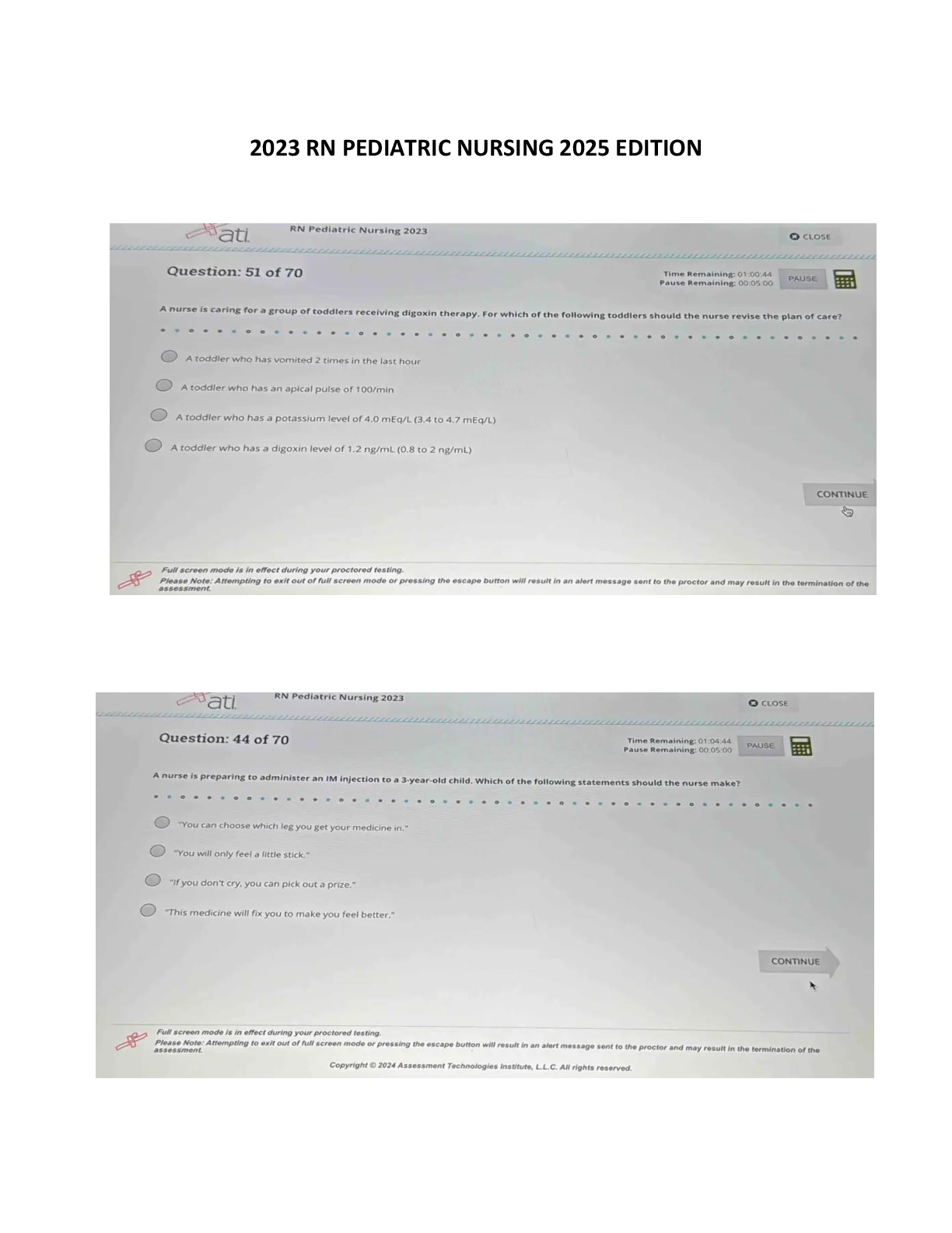
RN Pediatric Nursing Comprehensive Exam Study Guide
$ 20

CHE PHYSICAL- Amino acid and protein chemistry
$ 9

2022 AHIP FINAL EXAM_TEST.docx.docx.docx
$ 12

BUSN 311 Final Exam
$ 7

HIST 410N Final Exam Version 1 Questions with Answers GradeAplus
$ 20

ATI RN Leadership Management Proctored Exam.
$ 11

ATI Pharmacology Practice Version 3 | LATEST, Questions and Answers
$ 13

Latest Sophia - Human Biology - Unit 5 Challenge 4
$ 7

ATI Pharmacology Practice Questions Hematologic, Cardiovascular, Pain and Inflammation
$ 11.5

Strayer UniversitySOPHIA LEA DEVELOPINGsophia public speaking unit 1
$ 9
.png)
Human Resources Management (DECA) Questions and Answers Already Passed




























