EC 270 Midterm 1 Exam | Q & A (Complete Solutions)

Document Content and Description Below

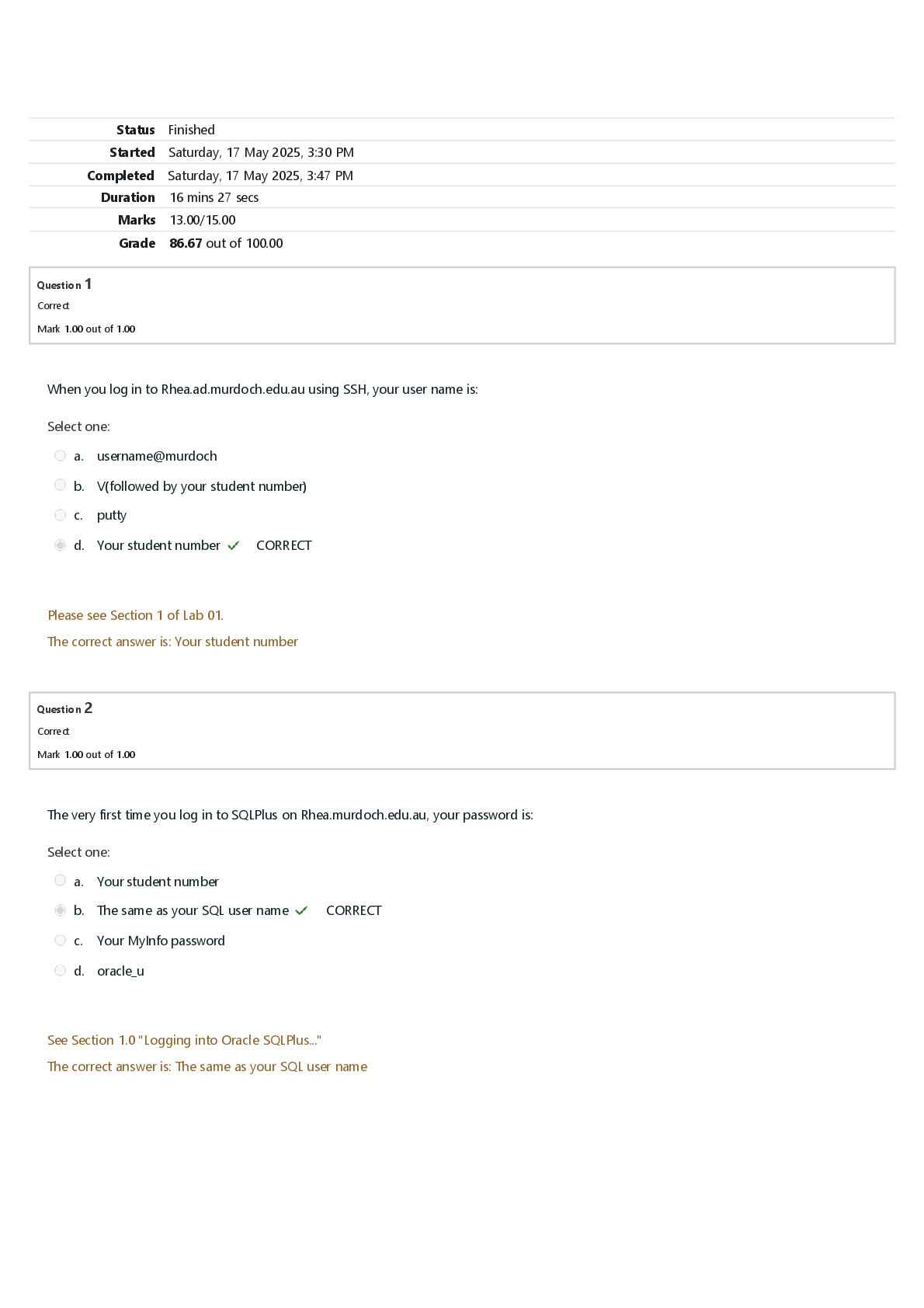
EC 270 Midterm 1 Exam | Q & A (Complete Solutions) Charlie has the utility function U(xA, xB) = xAxB. His indifference curve passing through 6 apples and 16 bananas will also pass through the point... where he consumes 2 apples and: a. 12 bananas b. 24 bananas c. 50 bananas d. 54 bananas e. 48 bananas Charlie has the utility function U(xA, xB) = xAxB. His indifference curve passing through 24 apples and 6 bananas will also pass through the point where he consumes 4 apples and a. 12 bananas. b. 40 bananas. c. 24 bananas. d. 43 bananas. e. 36 bananas Ambrose has the utility function U(x1, x2) = 4x^(1/2) + x2. If Ambrose were initially consuming 49 units of nuts (good 1) and 12 units of berries (good 2), then what is the largest number of berries that he would be willing to give up in return for an additional 32 units of nuts? a. 9 b. 21 c. 8 d. 4 e. 2 Ambrose has the utility function U(x1, x2) = 4x^(1/2) + x2. If Ambrose were initially consuming 81 units of nuts (good 1) and 22 units of berries (good 2), then what is the largest number of berries that he would be willing to give up in return for an additional 40 units of nuts? a. 4 b. 8 c. 11 d. 33 e. 2 Ambrose has the utility function U(x1, x2) = 4x^(1/2) + x2. If Ambrose were initially consuming 4 units of nuts (good 1) and 27 units of berries (good 2), then what is the largest number of berries that he would be willing to give up in return for an additional 21 units of nuts? a. 5 b. 12 c. 6 d. 32 e. 3 Joe Bob has a cousin Don who consumes goods 1 and 2. Don thinks that 3 units of good 1 is always a perfect substitute for 2 units of good 2. Which of the following utility functions is the only one that would not represent Don's preferences? a. U(x1, x2) = min{2x1, 3x2}. b. U(x1, x2) = 20x1 + 30x2 - 10,000. c. U(x1, x2) = 2x1 + 3x2 + 1000. d. U(x1, x2) = 4x21 + 12x1x2 + 9x22. e. More than one of the above does not represent Don's preferences. Harry Mazzola has the utility function U(x1, x2) = min{x1 + 2x2, 2x1 + x2}. He has $40 to spend on corn chips and French fries. If the price of corn chips is $2 per unit and the price of French fries is $2 per unit, then Harry will a. Definitely spend all of his income on corn chips. b. Consume at least as many french fries as corn chips but might consume both. c. Consume at least as many corn chips as french fries but might consume both. d. Definitely spend all of his income on french fries. e. Consume equal amounts of french fries and corn chips. . Harry Mazzola has the utility function U(x1, x2) = min{x1 + 2x2, 2x1 + x2}. He has $40 to spend on corn chips and french fries. If the price of corn chips is $1 per unit and the price of french fries is $4 per unit, then Harry will a. Consume at least as many corn chips as french fries but might consume both. b. Consume at least as many french fries as corn chips but might consume both. c. Definitely spend all of his income on french fries. d. Definitely spend all of his income on corn chips. e. consume equal amounts of french fries and corn chips. Phil Rupp, , has a sister Ethel who has the utility function U(x, y) = min{3x + y, 4y}. Where x is measured on the horizontal axis and y on the vertical axis, her indifference curves consist of a a. Positively sloped line segment and a negatively sloped line segment that meet along the line x = y. b. Vertical line segment and a horizontal line segment that meet in a kink along the line y = 3x. c. Horizontal line segment and a negatively sloped line segment that meet in a kink along the line x = y. d. Vertical line segment and a horizontal line segment that meet in a kink along the line x = 3y. e. Horizontal line segment and a positively sloped line segment that meet in a kink along the line x = 3y. Ike's utility function is U(x, y) = 25xy. He has 12 units of good x and 8 units of good y. Ben's utility function for the same two goods is U(x, y) = 4x + 4y. Ben has 9 units of x and 13 units of y. a. Ike prefers Ben's bundle to his own bundle, but Ben prefers his own bundle to Ike's. b. Ben prefers Ike's bundle to his own, but Ike prefers his own bundle to Ben's. c. Each prefers the other's bundle to his own. d. Neither prefers the other's bundle to his own. e. Since they have different preferences, there is not enough information to determine who envies whom. Jean-Pierre has preferences represented by the utility function U(x, y) = min{2x + y,x + 6y}. If x is on the horizontal axis and y is on the vertical axis, what is the slope of his indifference curve at the point (7,7)? a. -1/2 b. -6/2 c. -1/6 d. -2 e. -7/7 Mac's utility function is U(x, y) = max{2x - y, 2y - x}. a. Mac's preferences are quasilinear. b. If Mac has more x than y, any increase in his consumption of y would lower his utility. c. If Mac has more x than y, a decrease in his consumption of y would raise his utility. d. Mac always prefers more of each good to less. e. Goods x and y are perfect substitutes. Charles's utility function is U(x, y) = xy. Anne's utility function is U(x, y) = 1,000xy. Diana's utility function is -xy. Elizabeth's utility function is U(x, y) = -1/(xy + 1). Fergie's utility function is xy -10,000. Margaret's utility function is x/y. Philip's utility function is x(y + 1). (The goods x and y are two very expensive goods. We leave you to speculate about what they are.) Which of these persons have the same preferences as Charles? a. Everybody except Diana b. Anne and Fergie c. Anne, Fergie, and Elizabeth d. None of them e. All of them Raymond's preferences are represented by the utility function U(x, y) = x/y if y > 0 and U(x, y) = 0 if y = 0. a. Raymond has indifference curves that are rectangular hyperbolas. b. Raymond prefers more of each good to less. c. Raymond has quasilinear preferences. d. Raymond has a bliss point. e. Raymond has indifference curves that are upward-sloping straight lines if y > 0. Henry's utility function is x2 + 16xw + 64w2, where x is his consumption of x and wis his consumption of w. a. Henry's preferences are nonconvex. b. Henry's indifference curves are straight lines. c. Henry has a bliss point. d. Henry's indifference curves are hyperbolas. e. None of the above. Josephine's utility function is U(x, y) = y + 5x.5. She has 1 unit of x and 2 units of y. If her consumption of x is reduced to zero, how much y must she have in order to be exactly as well off as before? a. 14 units b. 9 units c. 11 units d. 7 units e. None of the above. Harmon's utility function is U(x1, x2) = x1x2. His income is $100. The price of good 2 is p2 = 4. Good 1 is priced as follows. The first 15 units cost $4 per unit and any additional units cost $2 per unit. What consumption bundle does Harmon choose? a. (12.5, 12.5) b. (25, 12.5) c. (12.5, 25) d. (15, 10) e. None of the above. Oswald Odd consumes only goods 1 and 2. His utility function is U(x1, x2) = x1 + x2 +min{x1, x2}. Each of Oswald's indifference curves is a. L-shaped. b. made up of three line segments with slopes -2, -1, and -1/2. c. made up of two line segments with slopes -2 and -1/2. d. is smooth and has no kinks. e. is a diamond-shaped figure consisting of four line segments. Emily's utility function is U(x, y) = 3min{x, y} + y. If we draw her indifference curves with x on the horizontal axis and y on the vertical axis, these indifference curves are a. made up of two line segments that meet where x = 4y. One of these line segments is vertical and the other has slope -1. b. L-shaped with kinks where x = 4y. c. L-shaped with kinks where x = y. d. made up of two line segments that meet where x = y. One of these line segments is horizontal and the other has slope -3. e. V-shaped with kinks where x = 3y. Charlie has the utility function U(xA, xB) = xAxB. His indifference curve passing through 35 apples and 18 bananas will also pass through the point where he consumes 5 apples and a. 131 bananas. b. 137 bananas. c. 21 bananas. d. 42 bananas. e. 126 bananas. Charlie's utility function is U(A, B) = AB, where A and B are the numbers of apples and bananas, respectively, that he consumes. When Charlie is consuming 15 apples and 90 bananas, if we put apples on the horizontal axis and bananas on the vertical axis, the slope of his indifference curve at his current consumption is a. 215. b. -6. c. -12. d. -1/6. e. -1/12. Ambrose has the utility function U(x1, x2) = 4x1/21 + x2. If Ambrose is initially consuming 64 units of nuts and 10 units of berries, then what is the largest number of berries that he would be willing to give up in return for an additional 17 units of nuts? a. 9 b. 19 c. 4 d. 2 e. 1 Ambrose has the utility function U(x1, x2) = 4x1/21 + x2. If Ambrose is initially consuming 25 units of nuts and 17 units of berries, then what is the largest number of berries that he would be willing to give up in return for an additional 39 units of nuts? a. 8 b. 12 c. 25 d. 6 e. 3 Joe Bob's cousin Peter consumes goods 1 and 2. Peter thinks that 4 units of good 1 is always a perfect substitute for 2 units of good 2. Which of the following utility functions is the only one that would not represent Peter's preferences? a. U(x1, x2) = min{2x1, 4x2}. b. U(x1, x2) = 20x1 + 40x2 - 10,000. c. U(x1, x2) = 2x1 + 4x2 + 1,000. d. U(x1, x2) = 4x21 + 16x1x2 + 16x22. e. More than one of the above does not represent Peter's preferences. Phil Rupp's sister Ethel has the utility function U(x, y) = min{4x + y, 5y}. Where x is measured on the horizontal axis and y on the vertical axis, her indifference curves consist of a a. vertical line segment and a horizontal line segment which meet in a kink along the line y = 4x. b. vertical line segment and a horizontal line segment which meet in a kink along the line x = 4y. c. horizontal line segment and a negatively sloped line segment which meet in a kink along the line x = y. d. positively sloped line segment and a negatively sloped line segment which meet along the line x = y. e. horizontal line segment and a positively sloped line segment which meet in a kink along the line x = 4y. Charlie's indifference curves have the equation xB = constant/xA, where larger constants correspond to better indifference curves. Charlie strictly prefers the bundle (5, 14) to the bundle a. (6, 13). b. (14, 5). c. (11, 11). d. All of the above. e. None of the above. Ambrose has indifference curves with the equation x2 = constant - 4x^(1/2)1, where larger constants correspond to higher indifference curves. If good 1 is drawn on the horizontal axis and good 2 on the vertical axis, what is the slope of Ambrose's indifference curve when his consumption bundle is (4, 11)? a. -4/11 b. -11/4 c. -1 d. -13 e. -2 Ambrose has indifference curves with the equation x2 = constant - 4x^(1/2)1, where larger constants correspond to higher indifference curves. If good 1 is drawn on the horizontal axis and good 2 on the vertical axis, what is the slope of Ambrose's indifference curve when his consumption bundle is (1, 11)? a. -1/11 b. -11/1 c. -12 d. -2 e. -1 Nancy Lerner is taking a course from Professor Goodheart who will count only her best midterm grade and from Professor Stern who will count only her worst midterm grade. In one of her classes, Nancy has scores of 20 on her first midterm and 30 on her second midterm. When the first midterm score is measured on the horizontal axis and her second midterm score on the vertical, her indifference curve has a slope of zero at the point (20, 30). This class could a. be Professor Goodheart's but could not be Professor Stern's. b. be Professor Stern's but could not c. be Professor Goodheart's. not be either Professor Goodheart's or Professor Stern's. d. be either Professor Goodheart's or Professor Stern's. e. There is not enough information to tell whose class it could or couldn't be. if we graph Mary Granola's indifference curves with avocados on the horizontal axis and grapefruits on the vertical axis, then whenever she has more grapefruits than avocados, the slope of her indifference curve is -2. Whenever she has more avocados than grapefruits, the slope is -1/2. Mary would be indifferent between a bundle with 9 avocados and 15 grapefruits and another bundle with 15 avocados and a. 13 grapefruits. b. 11 grapefruits. c. 7 grapefruits. d. 9 grapefruits. e. 10 grapefruits. if we graph Mary Granola's indifference curves with avocados on the horizontal axis and grapefruits on the vertical axis, then whenever she has more grapefruits than avocados, the slope of her indifference curve is -2. Whenever she has more avocados than grapefruits, the slope is -1/2. Mary would be indifferent between a bundle with 9 avocados and 21 grapefruits and another bundle with 19 avocados and a. 7 grapefruits. b. 17 grapefruits. c. 10 grapefruits. d. 13 grapefruits. e. 11.50 grapefruits. if we graph Mary Granola's indifference curves with avocados on the horizontal axis and grapefruits on the vertical axis, then whenever she has more grapefruits than avocados, the slope of her indifference curve is -2. Whenever she has more avocados than grapefruits, the slope is -1/2. Mary would be indifferent between a bundle with 24 avocados and 30 grapefruits and another bundle with 30 avocados and a. 22 grapefruits. b. 24 grapefruits. c. 26 grapefruits. d. 28 grapefruits. e. 25 grapefruits. Tommy Twit's mother measures the departure of any bundle from her favorite bundle for Tommy by the sum of the absolute values of the differences. Her favorite bundle for Tommy is (2, 7), that is, 2 cookies and 7 glasses of milk. Tommy's mother's indifference curve that passes through the point (c, m) = (5, 4) also passes through a. the point (8, 1). b. the points (2, 1), (8, 7), and (5, 10). c. the point (2, 7). d. the points (5, 7), (2, 4), and (2, 10). e. None of the above. Tommy Twit's mother measures the departure of any bundle from her favorite bundle for Tommy by the sum of the absolute values of the differences. Her favorite bundle for Tommy is (2, 7), that is, 2 cookies and 7 glasses of milk. Tommy's mother's indifference curve that passes through the point (c, m) = (4, 5) also passes through a. the points (2, 3), (6, 7), and (4, 9). b. the point (6, 3). c. the point (2, 7). d. the points (4, 7), (2, 5), and (2, 9). e. None of the above. Tommy Twit's mother measures the departure of any bundle from her favorite bundle for Tommy by the sum of the absolute values of the differences. Her favorite bundle for Tommy is (2, 7), that is, 2 cookies and 7 glasses of milk. Tommy's mother's indifference curve that passes through the point (c, m) = (4, 5) also passes through a. the points (4, 7), (2, 5), and (2, 9). b. the point (2, 7). c. the point (6, 3). d. the points (2, 3), (6, 7), and (4, 9). e. None of the above. Tommy Twit's mother measures the departure of any bundle from her favorite bundle for Tommy by the sum of the absolute values of the differences. Her favorite bundle for Tommy is (2, 7), that is, 2 cookies and 7 glasses of milk. Tommy's mother's indifference curve that passes through the point (c, m) = (5, 4) also passes through a. the points (2, 1), (8, 7), and (5, 10). b. the point (2, 7). c. the point (8, 1). d. the points (5, 7), (2, 4), and (2, 10). e. None of the above. Charlie's indifference curves have the equation xB = constant/xA, where larger constants correspond to better indifference curves. Charlie strictly prefers the bundle (10, 15) to the bundle a. (15, 10). b. (11, 14). c. (12, 13). d. More than one of these options are correct. e. None of the above are correct. Charlie's indifference curves have the equation xB = constant/xA, where larger constants correspond to better indifference curves. Charlie strictly prefers the bundle (6, 15) to the bundle a. (12, 11). b. (7, 14). c. (15, 6). d. More than one of these options are correct. e. None of the above are correct. Charlie's indifference curves have the equation xB = constant/xA, where larger constants correspond to better indifference curves. Charlie strictly prefers the bundle (5, 11) to the bundle a. (11, 5). b. (6, 10). c. (8, 6). d. More than one of these options are correct. e. None of the above are correct. Angela consumes goods x and y. Her indifference curves are described by the formula y = k/(x + 3). Higher values of k correspond to better indifference curves. a. Angela prefers bundle (8, 9) to bundle (9, 8). b. Angela likes good y and hates good x. c. Angela prefers bundle (11, 9) to bundle (9, 11). d. Angela likes good x and hates good y. e. More than one of the above statements are true. Nick's indifference curves are circles, all of which are centered at (12, 12). Of any two indifference circles, he would rather be on the inner one than the outer one. a. Nick's preferences are not complete. b. Nick prefers (16, 17) to (10, 10). c. Nick prefers (10, 17) to (10, 10). d. Nick prefers (8, 8) to (17, 21). e. More than one of the above statements are true. If two goods are both desirable and preferences are convex, then a. there must be a kink in the indifference curves. b. indifference curves must be straight lines. c. if two bundles are indifferent, then an average of the two bundles is worse than either one. d. the marginal rate of substitution is constant along indifference curves. e. None of the above. If there are only two goods, if more of good 1 is always preferred to less, and if less of good 2 is always preferred to more, then indifference curves a. slope downward. b. slope upward. c. may cross. [Show More]

Last updated: 2 months ago

Preview 5 out of 22 pages