MATH 225 N Week 4 Probability Questions and Answers. Top Grade.

Document Content and Description Below

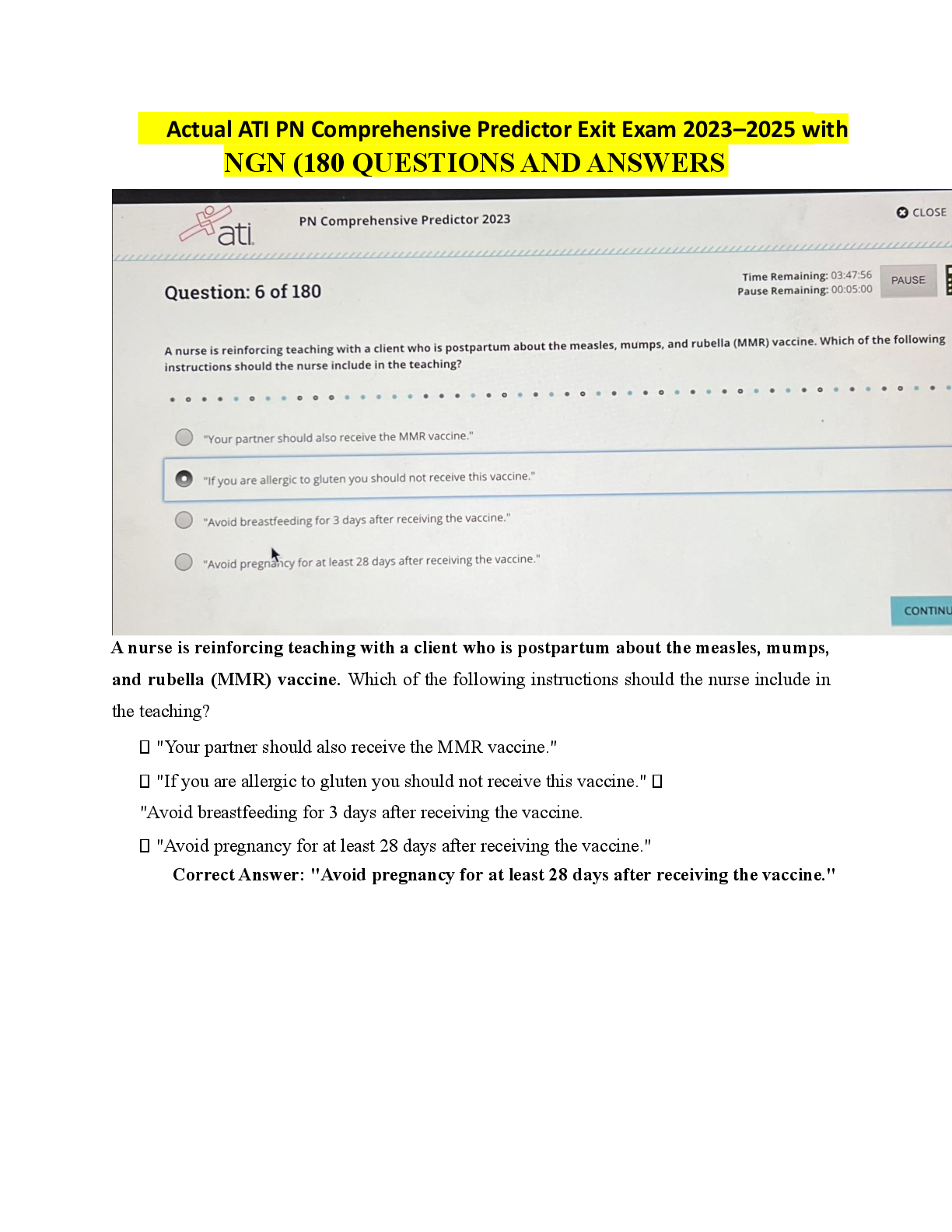
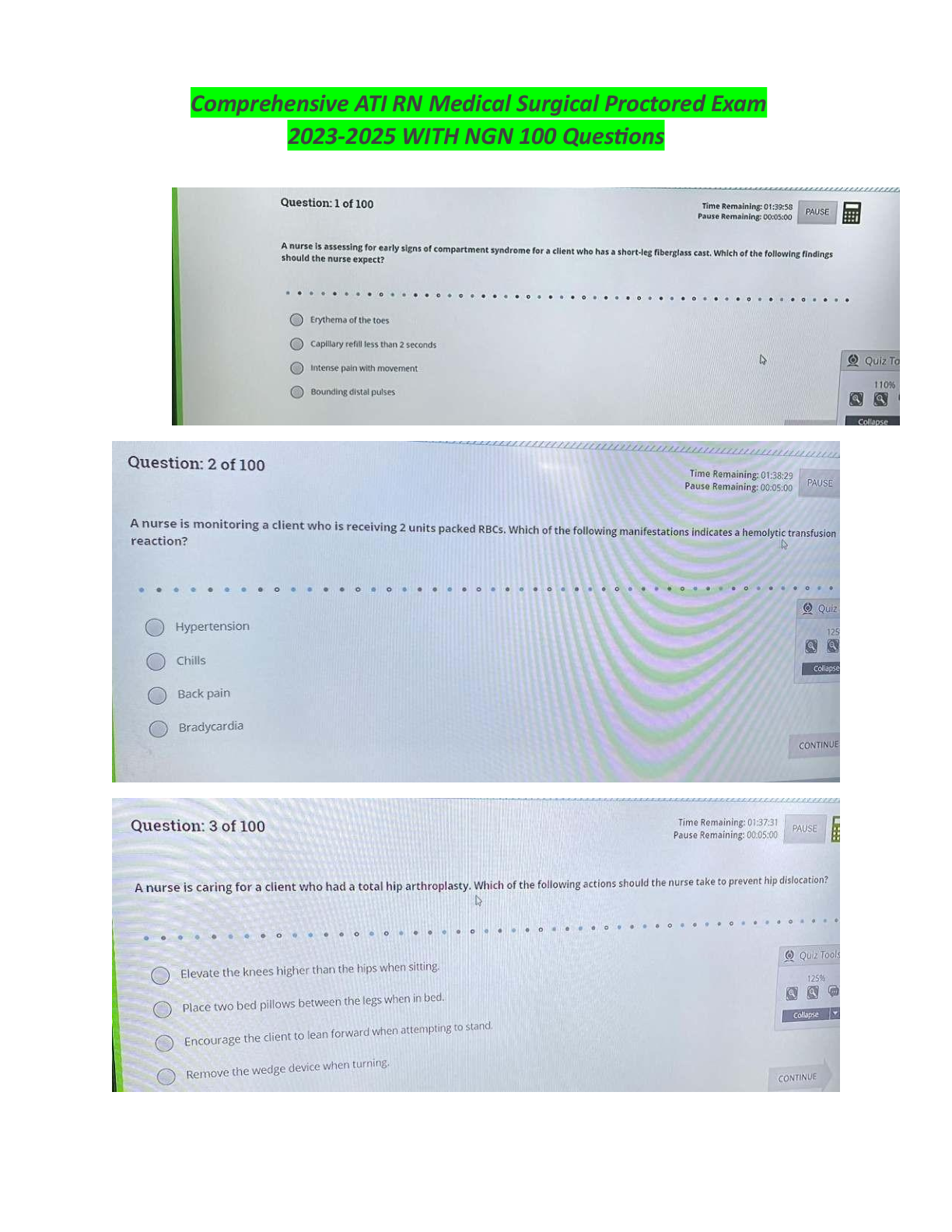
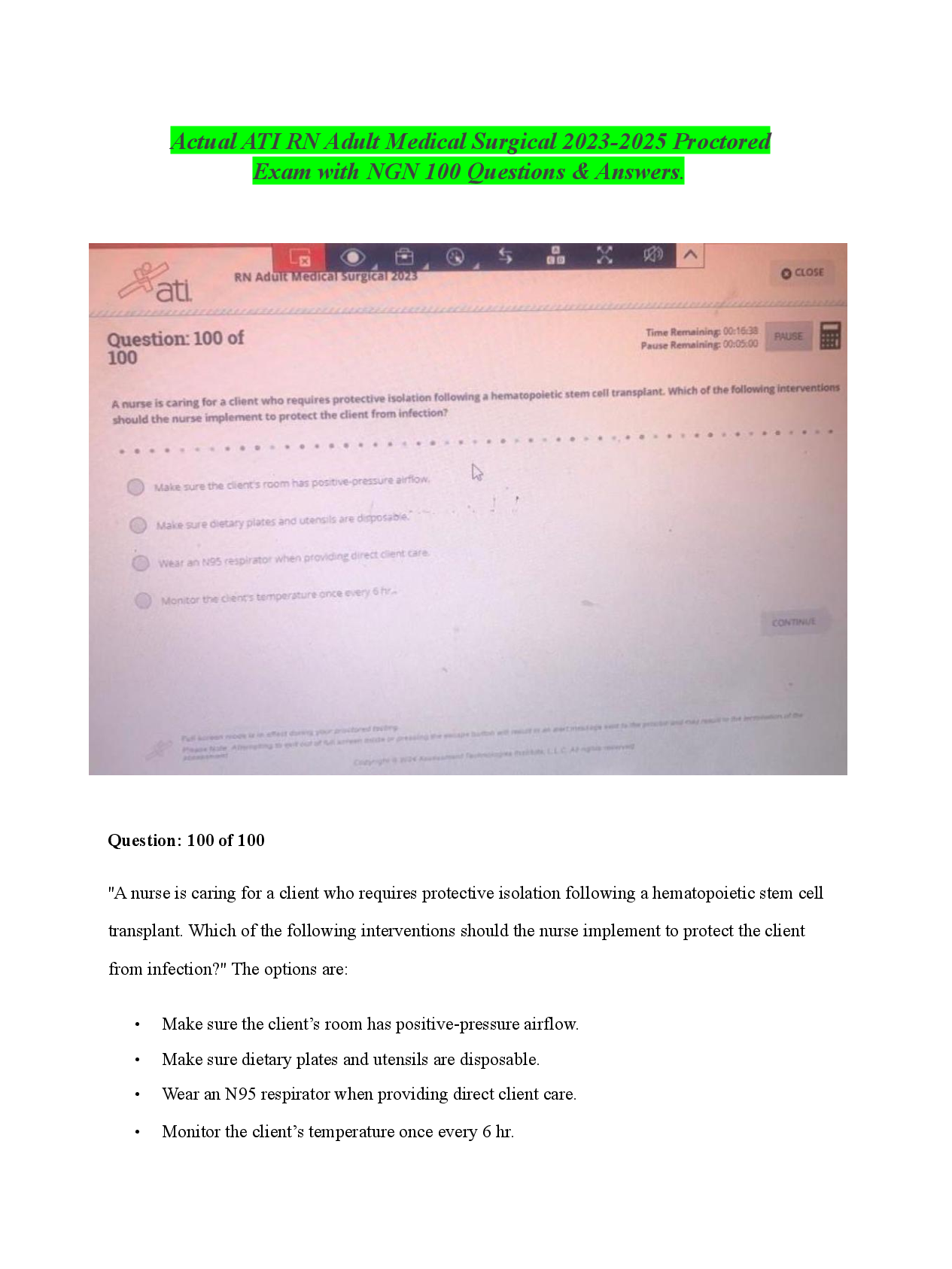
MATH 225 N Week 4 Probability Q&A Which of the pairs of events below is dependent? drawing a 7 and then drawing another 7 with replacement from a standard deck of cards rolling a 1 and ... then rolling a 6 with a standard die rolling a 3 and then rolling a 4 with a standard die drawing a heart and then drawing a spade without replacement from a standard deck of cards Identify the option below that represents dependent events. drawing a face card and then drawing a 3 without replacement from a standard deck of cards rolling a sum of 6 from the first two rolls of a standard die and a sum of 4 from the second two rolls drawing a 2 and drawing a 4 with replacement from a standard deck of cards drawing a heart and drawing another heart with replacement from a standard deck of cards Which of the following shows mutually exclusive events? rolling a sum of 9 from two rolls of a standard die and rolling 2 for the first roll drawing a red card and then drawing a black card with replacement from a standard deck of cards drawing a jack and then drawing a 7 without replacement from a standard deck of cards drawing a 7 and then drawing another 7 with replacement from a standard deck of cards Which of the pairs of events below is mutually exclusive? drawing an ace of spades and then drawing another ace of spades without replacement from a standard deck of cards drawing a 2 and drawing a 4 with replacement from a standard deck of cards drawing a heart and then drawing a spade without replacement from a standard deck of cards drawing a jack and then drawing a 7 without replacement from a standard deck of cards (Mutually exclusive events are events that cannot occur together. In this case, drawing an ace of spades and then drawing another ace of spades without replacement from a standard deck of cards are two events that cannot possibly occur together.) A deck of cards contains RED cards numbered 1,2,3,4,5,6, BLUE cards numbered 1,2,3,4,5, and GREEN cards numbered 1,2,3,4. If a single card is picked at random, what is the probability that the card has an ODD number? 10/15 8/15 14/15 6/15 Hector is a baseball fan but wants to watch something different. There are 5 basketball games, 2 football games, and 4hockey games that he can choose to watch. If Hector randomly chooses a game, what is the probability that it is a basketball game? There are 26 cards in a hat, each of them containing a different letter of the alphabet. card is chosen at random, what is the probability that it is not between the letters L and P, inclusive ? A spinner contains the numbers 1 through 80. What is the probability that the spinner will land on a number that is not a multiple of 12? An art collector wants to purchase a new piece of art. She is interested in 5 paintings, 6 vases, and 2 statues. If she chooses the piece at random, what is the probability that she selects a painting? Boris is taking a quiz for an online class. For the quiz, the system randomly assigns 2 high- difficulty questions, 7 moderate-difficulty questions, and 6 low-difficulty questions. What is the probability that Boris is assigned a moderate-difficulty question first? A spinner contains the numbers 1 through 40. What is the probability that the spinner will land on a number that is not a multiple of 6? Give your answer as a fraction. A spinner contains the numbers 1 through 50. What is the probability that the spinner will land on a number that is not a multiple of 4? Identify the parameters p and n in the following binomial distribution scenario. The probability of winning an arcade game is 0.718 and the probability of losing is 0.282. If you play the arcade game 20 times, we want to know the probability of winning more than 15 times. (Consider winning as a success in the binomial distribution.) A weighted coin has a 0.55 probability of landing on heads. If you toss the coin 14 times, what is the probability of getting heads exactly 9 times? (Round your answer to 3 decimal places if necessary.) Identify the parameter p in the following binomial distribution scenario. The probability of buying a movie ticket with a popcorn coupon is 0.546 and without a popcorn coupon is 0.454. If you buy 27 movie tickets, we want to know the probability that exactly 15 of the tickets have popcorn coupons. (Consider tickets with popcorn coupons as successes in the binomial distribution.) [Show More]

Last updated: 3 years ago

Preview 1 out of 27 pages