Basic Statistics > QUESTIONS & ANSWERS > ISYE 6644 FINAL PREP EXAM 2025 WITH REAL QUESTIONS AND 100% CORRECT ANSWERS | ALREADY GRADED A+ | (All)

ISYE 6644 FINAL PREP EXAM 2025 WITH REAL QUESTIONS AND 100% CORRECT ANSWERS | ALREADY GRADED A+ | GUARANTEED SUCCESS | ISYE 6644 ACTUAL LATEST EXAM 2025 [BRAND NEW]

Document Content and Description Below

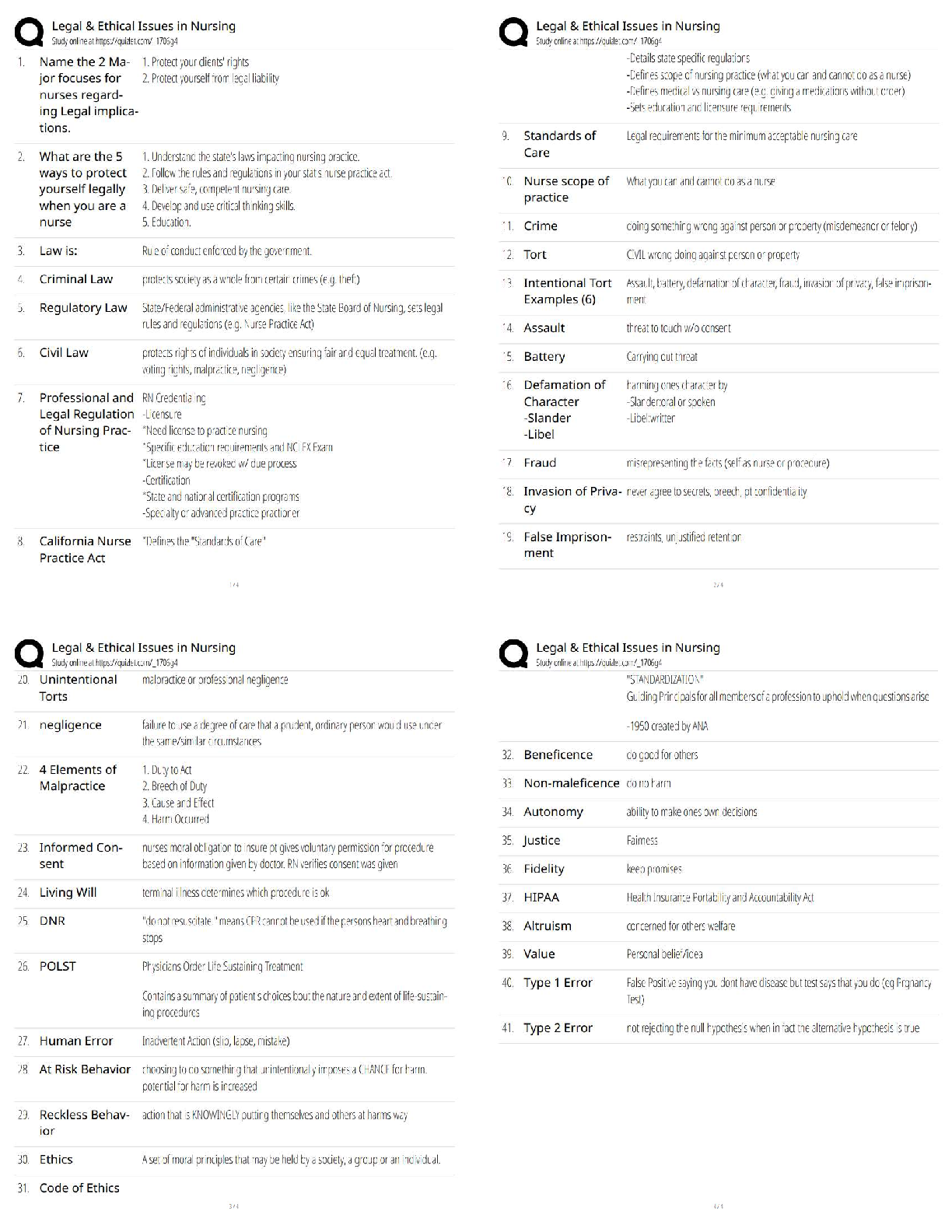
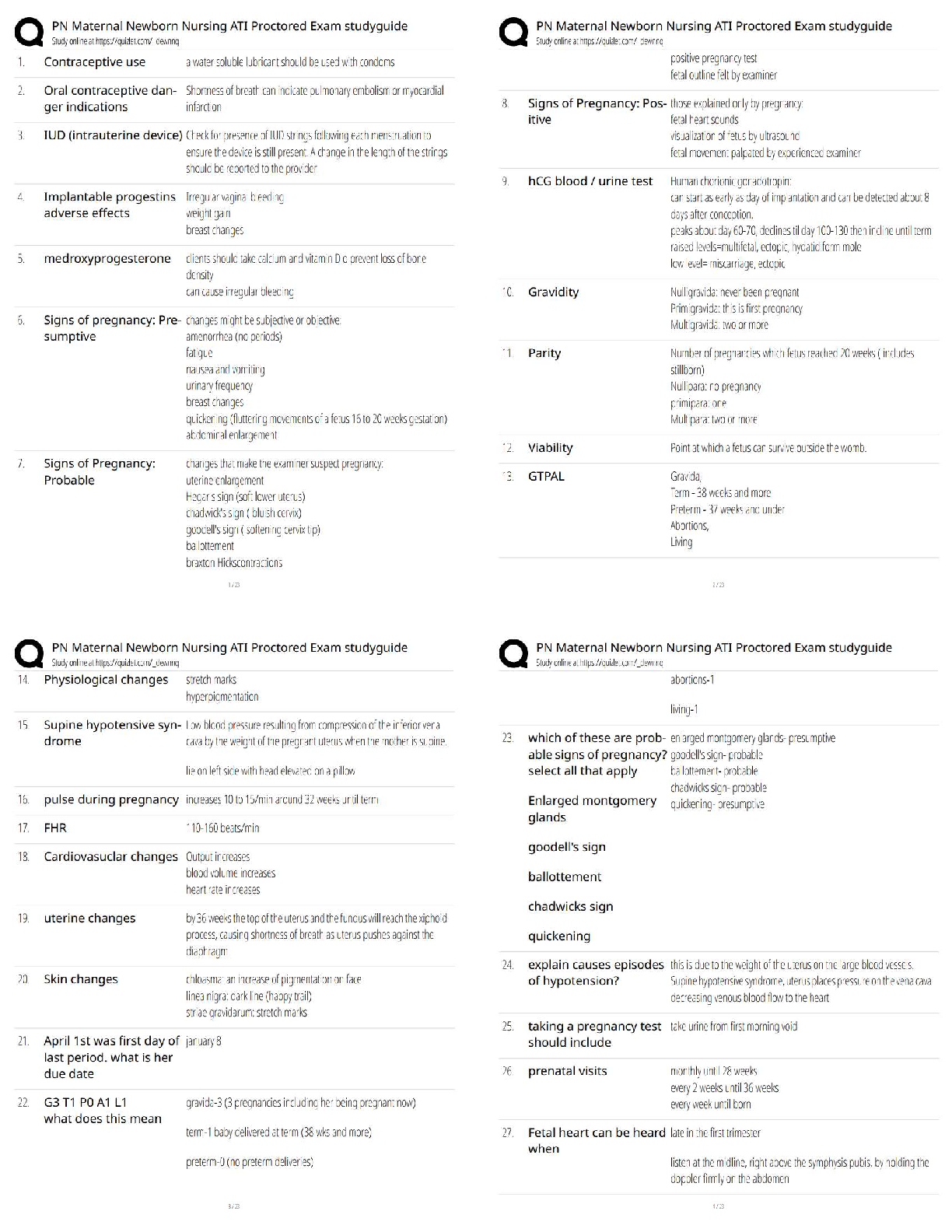
ISYE 6644 FINAL PREP EXAM 2025 WITH REAL QUESTIONS AND 100% CORRECT ANSWERS | ALREADY GRADED A+ | GUARANTEED SUCCESS | ISYE 6644 ACTUAL LATEST EXAM 2025 [BRAND NEW] What is a possible goa ... l of an indifference-zone normal means selection technique? - ANSWER- Find the normal population having the largest mean, especially if the largest mean is ≫ the second-largest. We are studying the waiting times arising from two queueing systems. Suppose we make 4 independent replications of both systems, where the systems are simulated independently of each other. replication system 1 system2 1 10 25 2 20 10 3 5 40 4 30 30 Assuming that the average waiting time results from each replication are approximately normal, find a two-sided 95% CI for the difference in the means of the two systems. - ANSWER- This is a two-sample CI problem assuming unknown and unequal variances. We have [-29.76, 9.76] This is sort of the same as Question 2, except we have now used common random numbers to induce positive correlation between the results of the two systems. Again find a two-sided 95% CI for the difference in the means of the two systems. - ANSWER- This is a paired-t CI problem assuming unknown variance of the differences. [-16.5, -3.5] [Show More]

Last updated: 4 months ago

Preview 4 out of 19 pages

Buy Now

Instant download

We Accept: