ATI TEAS Math Formulas. All Mathematics Formulas You Must Know! Taking the ATI TEAS test with only a few weeks or even few days to study.

Document Content and Description Below

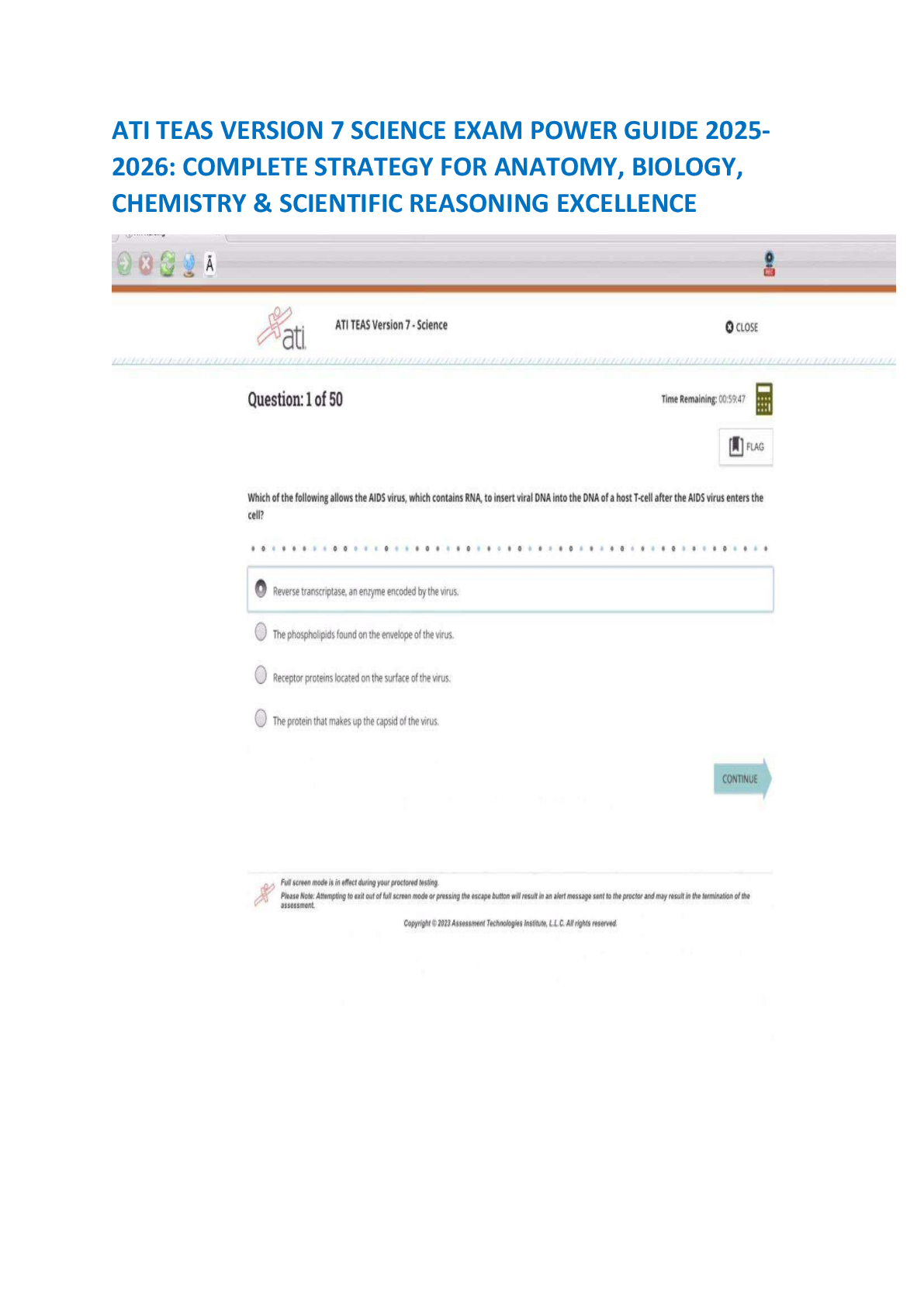
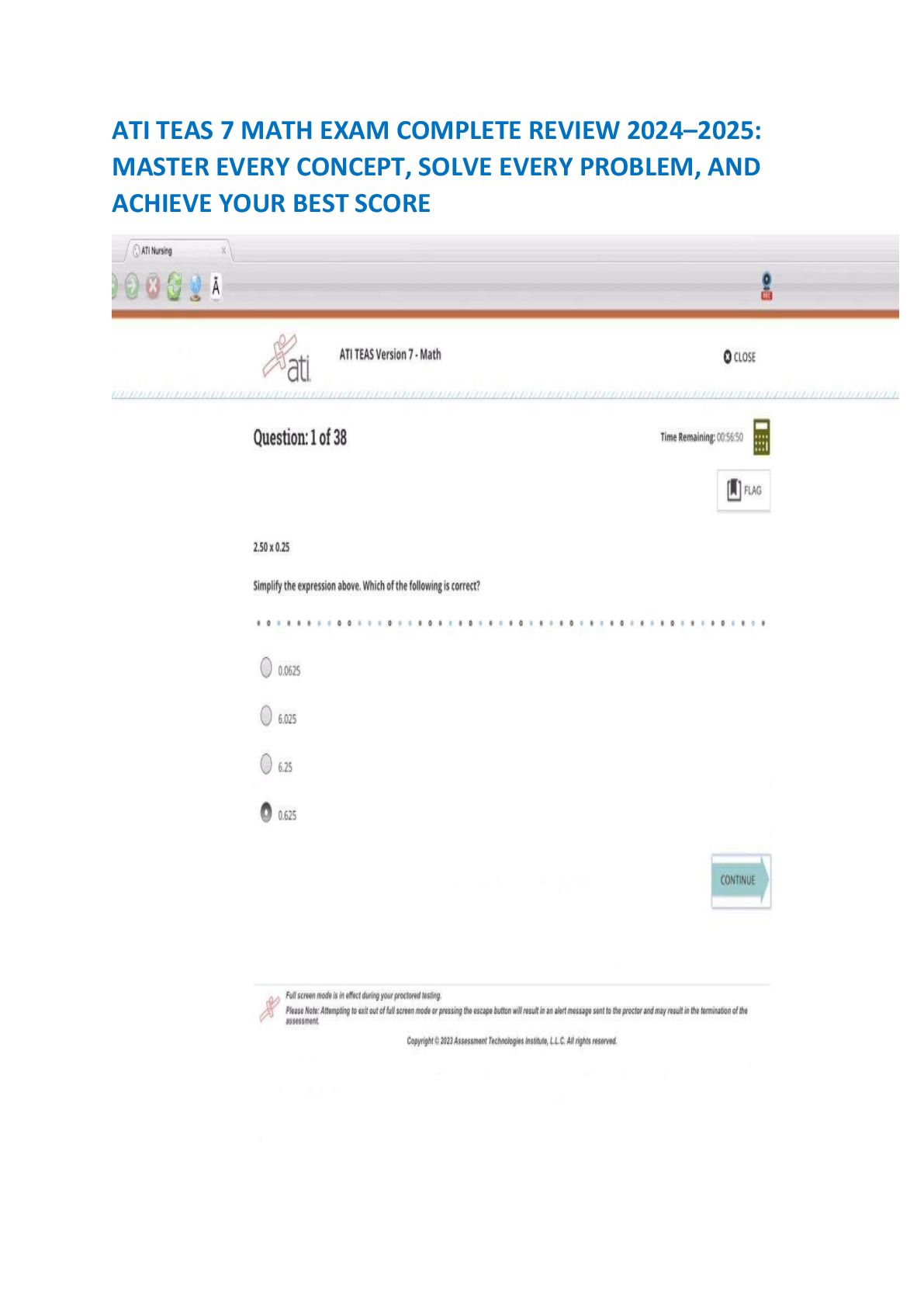
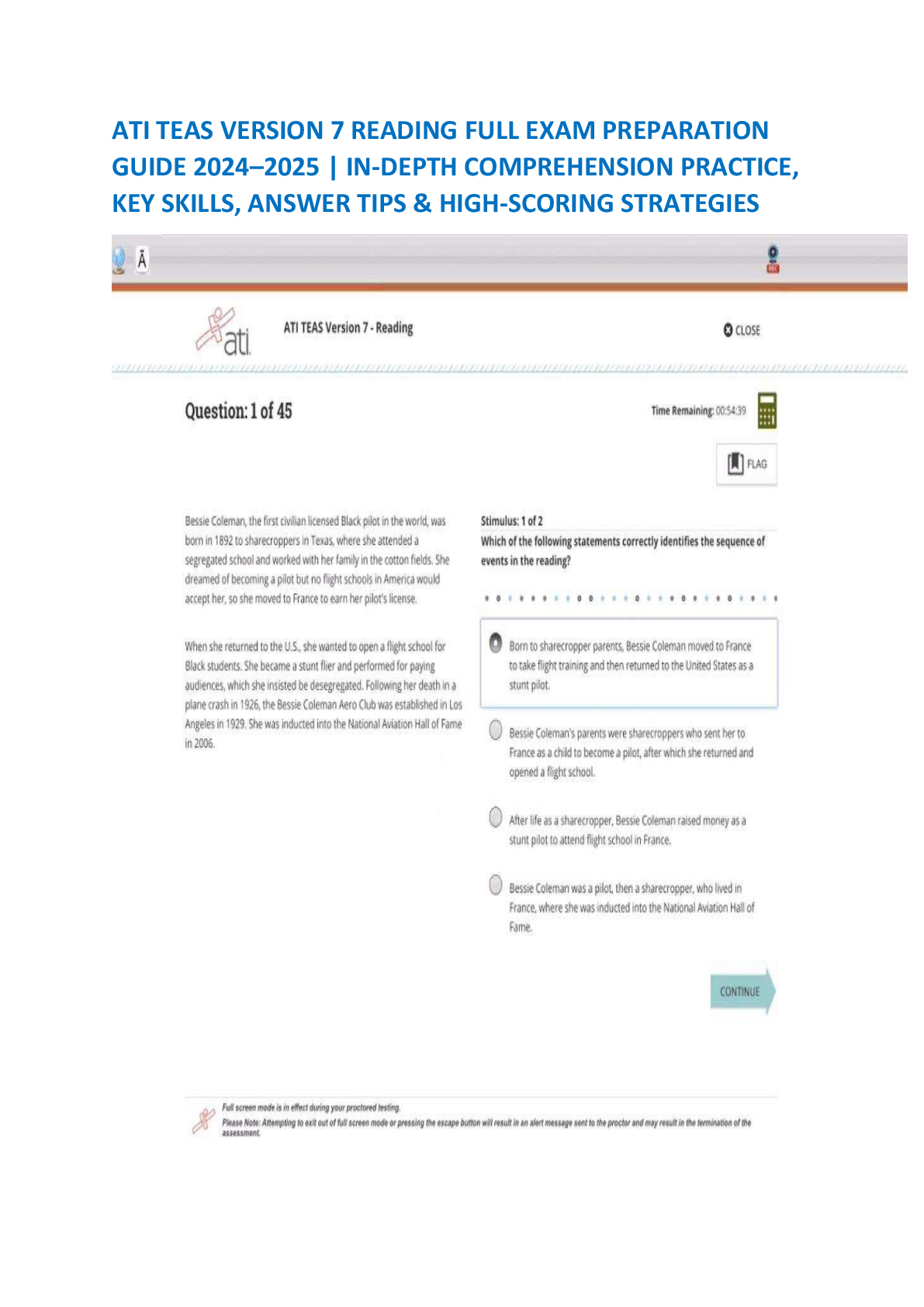
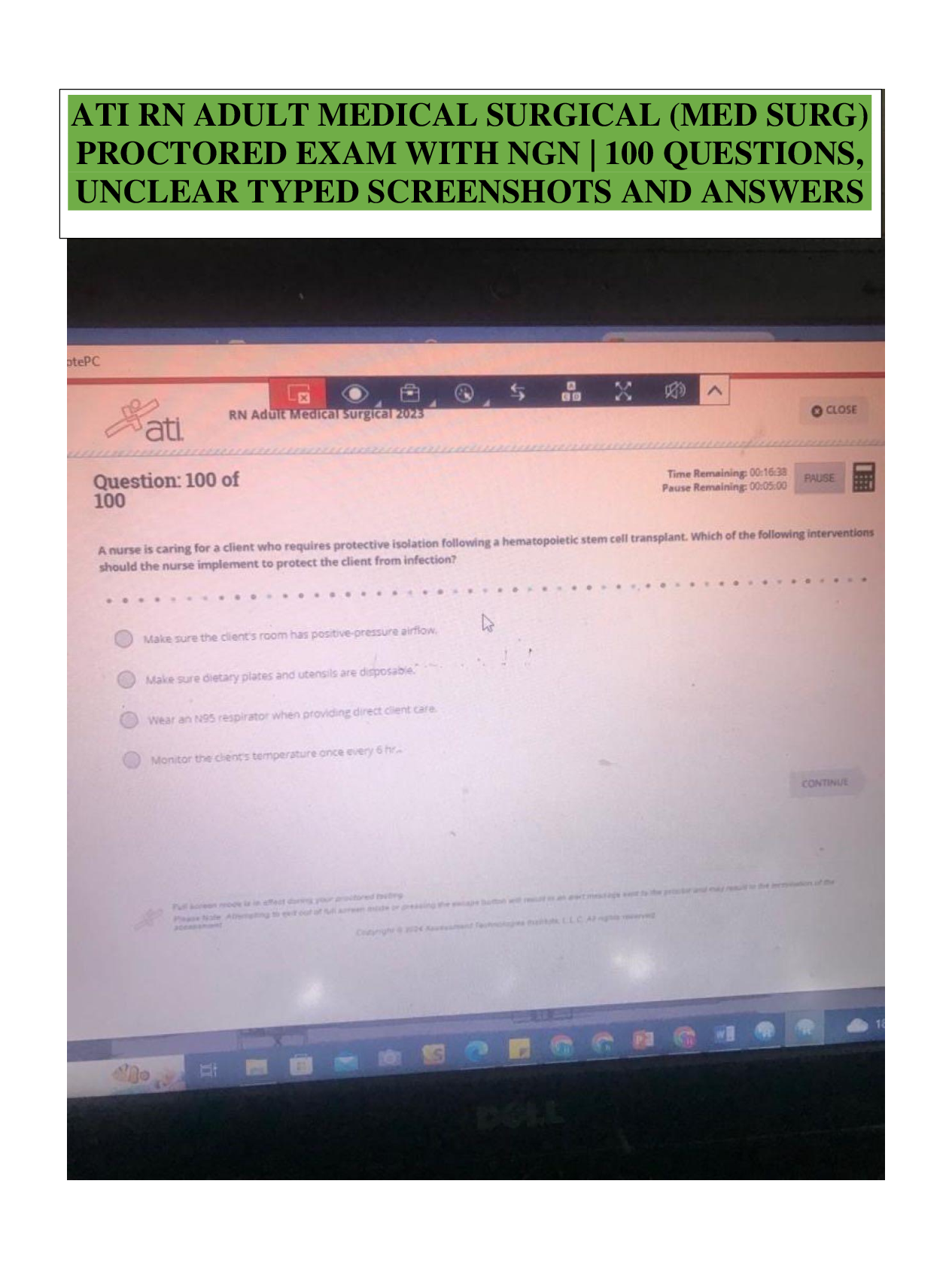
All Mathematics Formulas You Must Know! Taking the ATI TEAS test with only a few weeks or even few days to study? First and foremost, you should understand that the 2018 ATI TEAS Mathematics section ... does not provide a list of basic formulas that will be required to know for the test. This means that you will need to be able to recall many math formulas on the ATI TEAS. Below you will find a list of all Math formulas you MUST have learned before test day, as well as some explanations for how to use them and what they mean. Keep this list around for a quick reminder when you forget one of the formulas. Review them all, then take a look at the math topics to begin applying them! Mathematics Formula Sheet Place Value The value of the place, or position, of a digit in a number. Example: In 456, the 5 is in “tens” position. Fractions A number expressed in the form Adding and Subtracting with the same denominator: + = – = Adding and Subtracting with the different denominator: + = – = Multiplying and Dividing Fractions: × = ÷ = = Comparing Numbers Signs Equal to = Less than < Greater than > Greater than or equal ≥ Less than or equal ≤ Rounding Putting a number up or down to the nearest whole number or the nearest hundred, etc. Example: 64 rounded to the nearest ten is 60, because 64 is closer to 60 than to 70. Whole Number The numbers {0, 1, 2, 3, …} Mixed Numbers A number composed of a whole number and fraction Example: 2 Estimates Find a number close to the exact answer. Decimals is a fraction written in a Converting between special form. For example, improper fractions and mixed numbers: instead of writing you can write 0.5. a = a + = Factoring Numbers Factor a number means to break it up into numbers that can be multiplied together to get the original number. Example: 12 = 2 × 2 × 3 Divisibility Rules Divisibility means that you are able to divide a number evenly. Example: 24 is divisible by 6, because 24 ÷ 6 = 4 Greatest Common Factor Multiply common prime factors Example: 200 = 2 × 2 × 2 × 5 × 5 60 = 2 × 2 × 3 × 5 GCF (200, 60) = 2 × 2 × 5 = 20 Least Common Multiple Check multiples of the largest number Example: LCM (200, 60): 200 (no), 400 (no), 600 (yes!) Integers {… , –3, –2, –1, 0, 1, 2, 3, …} Includes: zero, counting numbers, and the negative of the counting numbers Real Numbers All numbers that are on number line. Integers plus fractions, decimals, and irrationals (√2, √3, π, etc.) Absolute Value Refers to the distance of a number from 0, the distances are positive as absolute value of a number cannot be negative. = 22 |x| = |x| < n ⇒ −n < x < n |x| > n ⇒ x < −n or x > n Order of Operations PEMDAS (parentheses / exponents / multiply / divide / add / subtract) Ratios A ratio is a comparison of two numbers by division. Example: 3: 5, or Proportional Ratios A proportion means that two ratios are equal. It can Percentages be written in two ways: use the following formula to find part, whole, or percent part = × whole Percent of Change × 100 % = , a: b = c: d Discount Multiply the regular price by the rate of discount Selling price = original price – discount Markup Markup = selling price – cost Markup rate = markup divided by the cost Expressions and Variables A variable is a letter that represents unspecified numbers. One may use a variable in the same manner as all other numbers: Tax To find tax, multiply the tax rate to the taxable amount (income, property value, etc.) Distributive Property Addition Subtraction Division 2 2 plus + a a y y – minus 3 3 4 divided by x a (b + c) = ab + ac Polynomial P(x) = a0xn + a1xn–1 + … + an–22x2 + an–1x + an Multiplication 5a 5 times a Systems of Equations Two or more equations working together. example: – 2x + 2y = 4 – 2x + y = 3 Equations The values of two mathematical expressions are equal. ax + b = c Solving Systems of Equations by Substitution Functions A function is a rule to go from one number (x) to another number (y), usually written y = f (x). For any given value of x, there can only be one corresponding value y. If y = kx for some number k (example: f (x) = 0.5 x), then y is said to be directly proportional to x. If y = k/x (example: f (x) = 5/x), then y is said to be inversely proportional to x. The graph of y = f (x h) + k is the translation of the graph of y = f (x) by (h, k) units in the plane. For example, y = f (x + 3) shifts the graph of f (x) by 3 units to the left. Consider the system of equations x – y = 1, –2x + y = 6 Substitute x = 1 – y in the second equation –2(1–y) + y = 5 y = 2 Substitute y = 2 in x = 1 + y X = 1 + 2 = 3 Solving Systems of Equations by Elimination 3y = 9 y = 3 x + 6 = 6 x = 0 Inequalities Says that two values are not equal a ≠ b a not equal to b a < b a less than b a > b a greater than b a ≥ b a greater than or equal b a ≤ b a less than or equal b Parallel lines Have equal slopes. Perpendicular lines (i.e., those that make a 90◦ angle where they intersect) have negative reciprocal slopes: m1 . m2 = −1. Intersecting Lines Lines (Linear Functions) Consider the line that goes through points A(x1, y1) and B(x2, y2). Distance from A to B: Mid–point of the segment AB: M( , ) Slope of the line: = Point–slope form: Given the slope m and a point (x1, y1) on the line, the equation of the line is (y − y1) = m (x − x1). Slope–intercept form: given the slope m and the y–intercept b, then the equation of the line is y = mx + b. Parallel Lines (l ǁm) Intersecting lines: opposite angles are equal. Also, each pair of angles along the same line add to 180◦. In the figure above, a + b = 180◦. Parallel lines: eight angles are formed when a line crosses two parallel lines. The four big angles (a) are equal, and the four small angles (b) are equal. Parabolas: A parabola parallel to the y– axis is given by y = ax2 + bx + c. If a > 0, the parabola opens up. If a < 0, the parabola opens down. The y–intercept is c, and the x–coordinate of the vertex is x = −b/2a. Factoring “FOIL” (x + a)(x + b) = x2 + (b + a)x + ab “Difference of Squares” a2 − b2 = (a + b)(a − b) “Reverse FOIL” x2 + (b + a)x + ab = (x + a) (x + b) You can use Reverse FOIL to factor a polynomial by thinking about two numbers a and b which add to the number in front of the x, and which multiply to give the constant. For example, to factor x2 + 5x + 6, the numbers add to 5 and multiply to 6, i.e.: a = 2 and b = 3, so that x2 + 5x + 6 = (x + 2)(x + 3). To solve a quadratic such as x2 +bx+c = 0, first factor the left side to get (x + a)(x +b) = 0, then set each part in parentheses equal to zero. For example, x2 + 4x + 3 = (x + 3)(x + 1) = 0 so that x = −3 or x = −1. To solve two linear equations in x and y: use the first equation to substitute for a variable in the second. E.g., suppose x + y = 3 and 4x − y = 2. The first equation gives y = 3 − x, so the second equation becomes 4x − (3 − x) = 2 ⇒ 5x − 3 = 2 ⇒ x = 1, y = 2. Exponents Refers to the number of times a number is multiplied by itself. 8 = 2 × 2 × 2 = 23 Scientific Notation It is a way of expressing numbers that are too big or too small to be conveniently written in decimal form. In scientific notation all numbers are written in this form: m × 10n Decimal notation Scientific notation 103 Square The number we get after multiplying an integer (not a fraction) by itself. Example: 2 × 2 = 4, 22 = 4 Square Roots A square root of x is a number r whose square is x : r2 = x r is a square root of x Pythagorean Theorem a2 + b2 = c2 All triangles: Triangles Right triangles: Area = b . h Angles on the inside of any triangle add up to 180◦. The length of one side of any triangle is always less than the sum and more than the difference of the lengths of the other two sides. An exterior angle of any triangle is equal to the sum of the two remote interior angles. Other important triangles: Equilateral: These triangles have three equal sides, and all three angles are 60◦. A good example of a right triangle is one with a = 3, b = 4, and c = 5, also called a 3– 4–5 right triangle. Note that multiples of these numbers are also right triangles. For example, if you multiply these numbers by 2, you get a = 6, b = 8, and Isosceles: An isosceles triangle has two equal sides. The “base” angles (the ones opposite the two sides) are equal (see the 45◦ triangle above). Similar: Two or more triangles are similar if they have the same shape. The corresponding angles are equal, and the corresponding sides are in proportion. For example, the 3–4–5 triangle and the 6–8–10 triangle from before are similar since their sides are in a ratio of 2 to 1. c = 10 (6–8–10), which is Rectangles also a right triangle. (Square if l = w) Area = lw Circles Area = πr2 Circumference = 2πr Full circle = 360◦ Parallelogram (Rhombus if l = w) Area = lh Regular polygons are n– Length Of Arc = (n◦/360◦) . sided figures with all 2πr sides equal and all angles Area Of Sector = (n◦/360◦) . equal. πr2 The sum of the inside angles of an n–sided regular Equation of the circle (above polygon is left figure): (x − h)2 + (y − k)2 (n − 2) . 180◦. = r2. Area of a parallelogram: A = bh Area of a trapezoid: A = h (b1 + b2) Surface Area and Volume of a rectangular/right prism: SA = ph + 2B V = Bh Solids Surface Area and Volume of a cylinder: SA = 2πrh + 2πr2 V = πr2h Rectangular Solid Volume = lwh Area = 2(lw + wh + lh) Surface Area and Volume of a Pyramid SA = ps + b V = bh Surface Area and Volume of a Cone SA = πrs + πr2 V = πr2h Surface Area and Volume of a Sphere SA = 4πr2 V = πr3 (p = perimeter of base B; π ~ 3.14 ) Quadratic formula Simple interest (I = interest, p = principal, r = rate, t = time) Right Cylinder Volume = πr2h Area = 2πr(r + h) mean: mode: value in the list that appears most often range: largest value – smallest value Arithmetic Sequences: Median Each term is equal to the Middle value in the list previous term plus d (which must be sorted) Example: median of Sequence: t1, t1 + d, t1 + 2d, . . . {3, 10, 9, 27, 50} = 10 Example: median of {3, 9, 10, 27} = = 9.5 Sum average × (number of terms) Average Average speed Fundamental Counting Principle: If an event can happen in N ways, and another, independent event can happen in M ways, then both events together can happen in N × M ways. (Extend this for three or more: N1 × N2 × N3 …) 1/xb= x – b (xa)b= xa.b (xy)a = xa . ya Polygon Parts x0 = 1 √xy = √x . √y (−1)n = −1, if n is odd. (−1)n = +1,if n is even. If 0 < x < 1, then 0 < x3 < x2 < x < √x < √3x < 1. Factorials Side one of the line segments that make up the polygon Factorial– the product of a number and all counting numbers below it. Vertex point where two sides meet. Two or more of these points are called vertices 8 factorial = 8! = 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 40,320 Diagonal a line connecting two vertices that isn't a side 5 factorial = 5! = 5 x 4 x 3 x 2 x 1 = 120 Interior Angle angle formed by two adjacent sides inside the polygon 2 factorial = 2! = 2 x 1 = 2 Exterior Angle angle formed by two adjacent sides outside the polygon Interest Multiplying Two Powers of the SAME Base When the bases are the same, you find the new power by just adding the exponents x a x b = x (a + b) Multiplying Two Powers of Different Bases Same Exponent If the bases are different but the exponents are the same, then you can combine them x a y a = (xy) a Powers of Powers For power of a power: you multiply the exponents. (xa) b = x (ab) Dividing Powers xa/xb = x a x –b = x a–b The Zero Exponent Anything to the 0 power is 1. x0 = 1 Measurements Metric millimeter (mm) ~ width of a dime centimeter (cm) ~ 1 finger sideways meter (m) ~ height of chair/guitar kilometer (km) ~ 10 min walk Customary inch (in) ~ width of 2 fingers foot (ft) ~ adult shoe yard (yd) ~ height of chair A negative exponent means to divide by that number of factors instead of multiplying. So 4–3 is the same as 1/(43), and x–3 = 1/x3. Conversions Square Units Larger to smaller units ––– multiply Smaller to larger units ––– divide 1 kg = 1000 g 1 g = 1000 mg kg → g multiply by 1000 g → mg mutliply by 1000 in2 → ft2 divide by 144 ft2 → in2 multiply by 144 ft2 → yd2 divide by 9 yd2 → ft2 multiply by 9 mg → g divide by 1000 g → kg divide by 1000 km → m mutltiply by 1000 m →cm multiply by 100 cm → mm multiply by 10 mm → cm divide by 10 cm → m divide by 100 m → km divide by 10 Other Helpful Measurements 16 oz = 1 lb 1 T = 2000 lb (T= ton) 2 cups = 1 pint Rules of Divisibility Classifying Angles Rules of divisibility by 2, 3, Corresponding 5, 9 and 10 Angles that are in the same position and are formed by a transversal cutting two or more parallel. 9 The sum of the digits is divisible by 9. 10 The ones digit is a 0. Two angles whose measures have a sum of 90° Geometry Terminology Angle A geometric figure formed by two rays that have a common endpoint. Congruent having the same size and shape. Intersecting Lines lines that cross at exactly one poin Line AE intersects line CD at point B. Line A set of points that extends without end in opposite directions. Solid Figure a three–dimensional figure Transversal a line that intersects two or more lines Line AB is a transversal. Vertex The point where two or more rays meet; the point of intersection of two sides of a polygon; the point of intersection of three or more edges of a solid figure; the top point of a cone. Ray A part of a line that has one endpoint and goes on forever in only one direction Polygon A closed plane figure formed by three or more line segments Plane Figure A figure which lies in a plane Plane A flat surface that goes on forever in all directions Edge The line segment where two faces of a solid figure meet Line Segment Part of a line with two endpoints Face One of the polygons of a solid figure The cube has 6 faces. Three– Dimensional Having length, width, and height The rectangular prism is three– dimensional. Cone A solid figure with a circular base and one vertex Base A side of a polygon or a face of a solid figure by which the figure is measured or named [Show More]

Last updated: 1 year ago

Preview 1 out of 20 pages