Computer Science > QUESTIONS & ANSWERS > University of California, San Diego_CSE 101_hw4W17solutions-EDITED BY EXPERTS -ALL ANSWERS CORRECT (All)

University of California, San Diego_CSE 101_hw4W17solutions-EDITED BY EXPERTS -ALL ANSWERS CORRECT

Document Content and Description Below

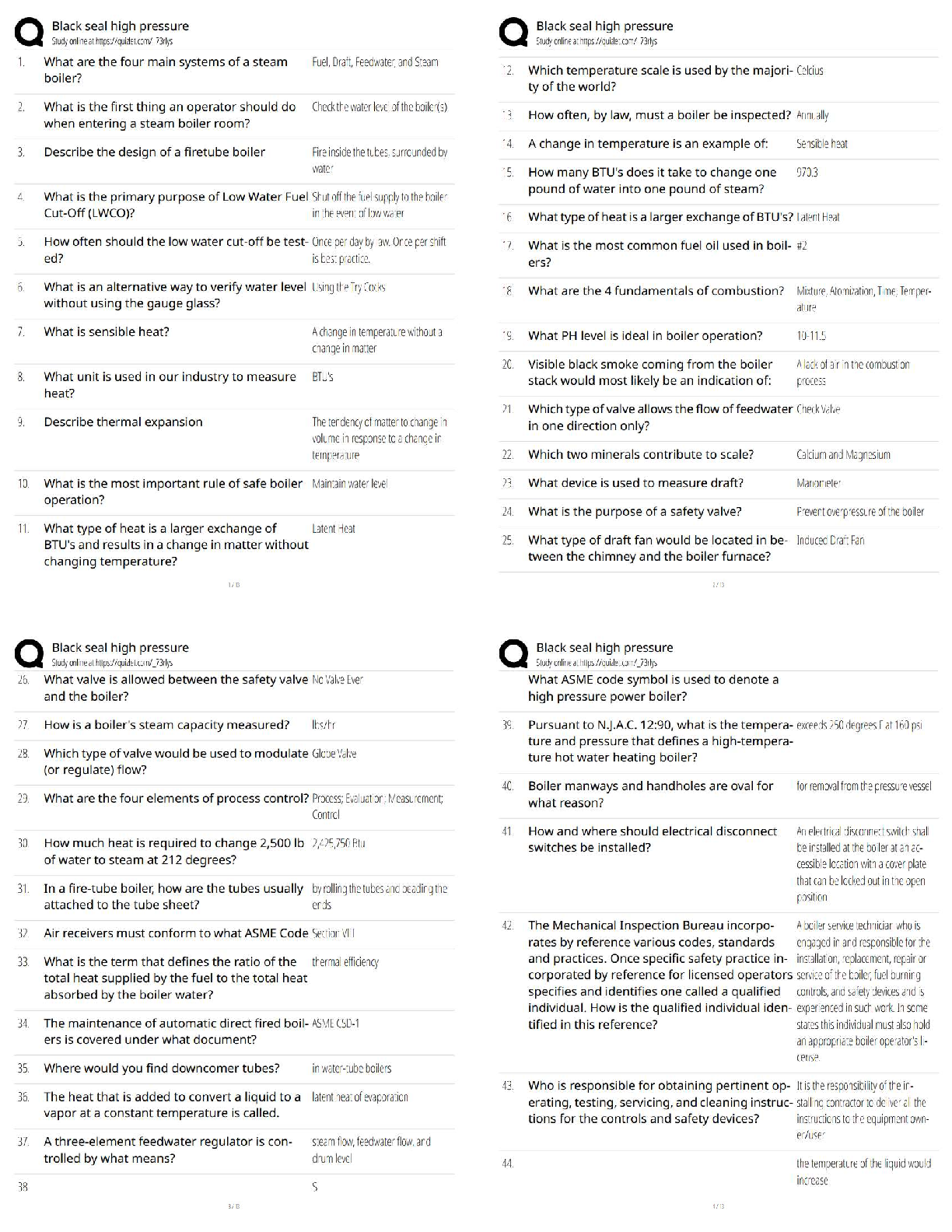
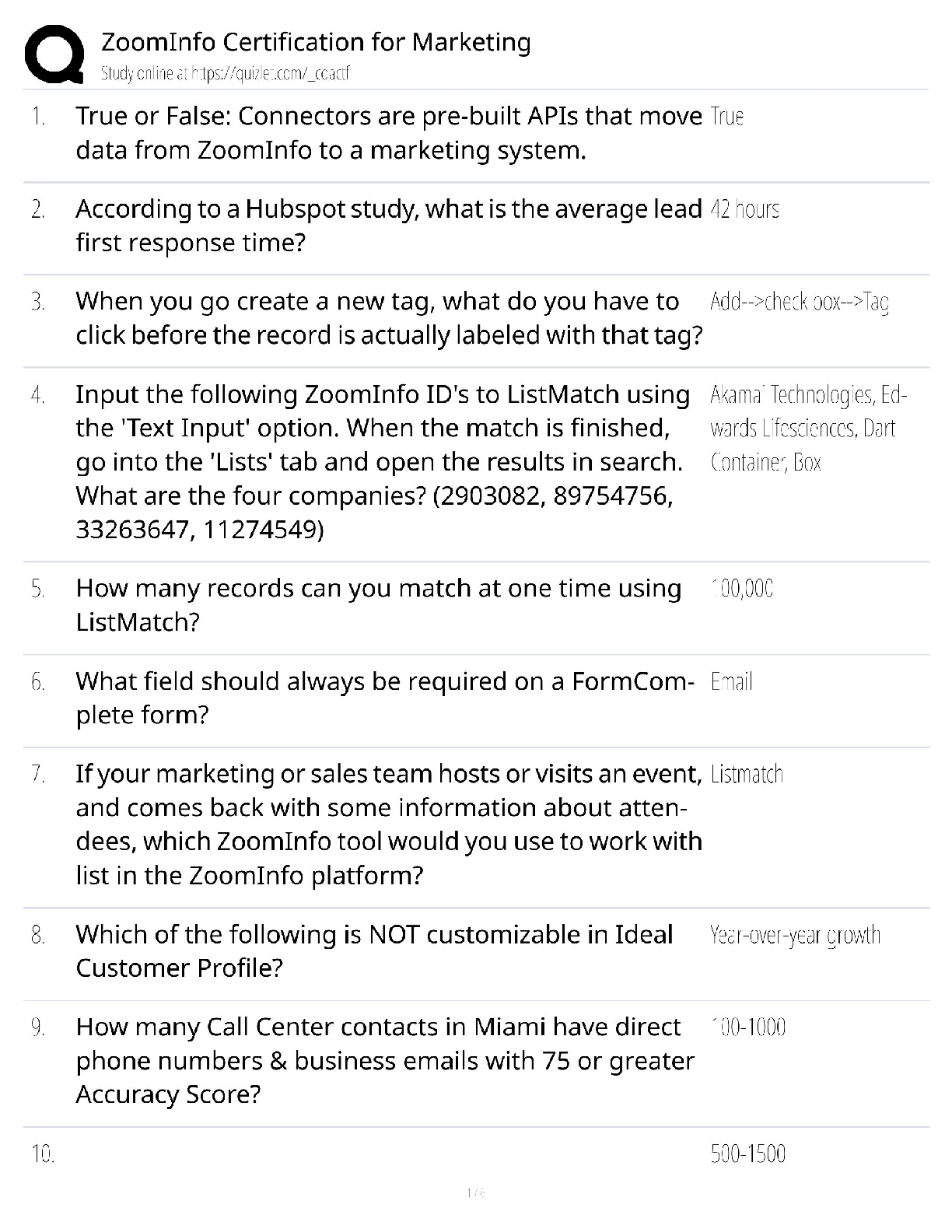
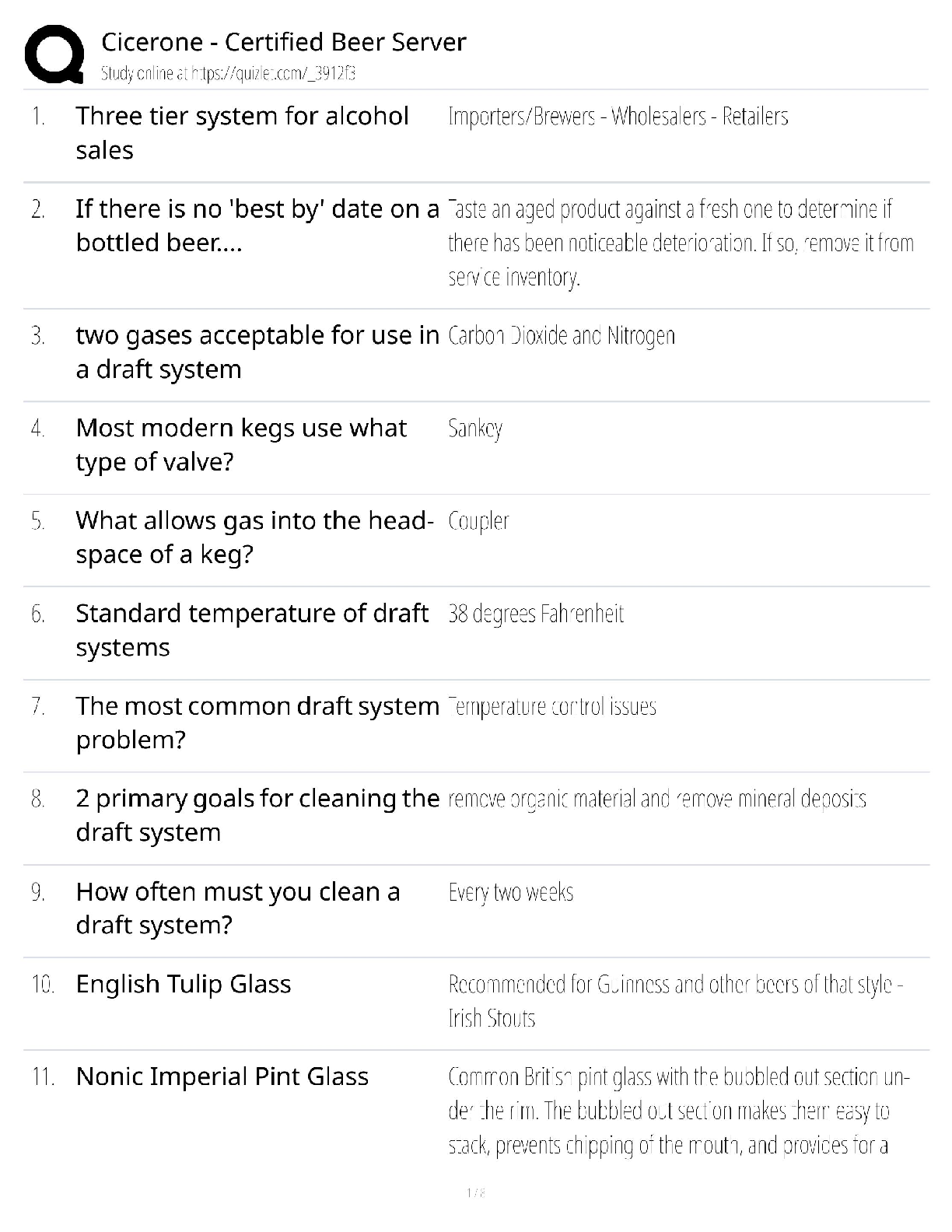
1. Suppose that your car can only hold enough gas to cover L miles. You are attempting to travel from city s to city t. The cities s = x0 and t = xk are at either end of a long straight road with som... e cities x1; : : : ; xk−1 between them. Let di be the distance between xi−1 and xi. It is known that jdij < L for all i. Assume you leave s with a full tank. You may have to stop to refuel your car on your way to t. You want to decide which cities to stop at so that you make it from s to t with the minimum number of stops. (a) State the greedy choice you could use to solve this problem efficiently. Choose the farthest reachable city from the starting point and repeat from your current city as a starting point. (b) Using your greedy choice from part (a), Write an algorithm that takes as input the distances d1; : : : ; dk and outputs the sequence of indices i1; : : : ; i‘ such that stopping at s; xi1; : : : ; xi‘; t will be a successful trip and ‘ is minimal. High level Description: Let j be the index such that jXi =1 di ≤ L ≤ j+1 Xi =1 di Output j (this is the index of the furthest city from s that is less than L miles away.) Repeat with xj as your starting city and t as your ending city. (Repeat on (dj+1; : : : ; dk)) Pseudocode: greedypath(d1; : : : ; dk) if k ≤ 1: return fg sum = 0 ind = 0 while sum < L: ind = ind + 1 sum = sum + dind return find-1g [ greedypath(dind-1; : : : ; dk) [Show More]

Last updated: 2 years ago

Preview 1 out of 7 pages

Buy Now

Instant download

We Accept: