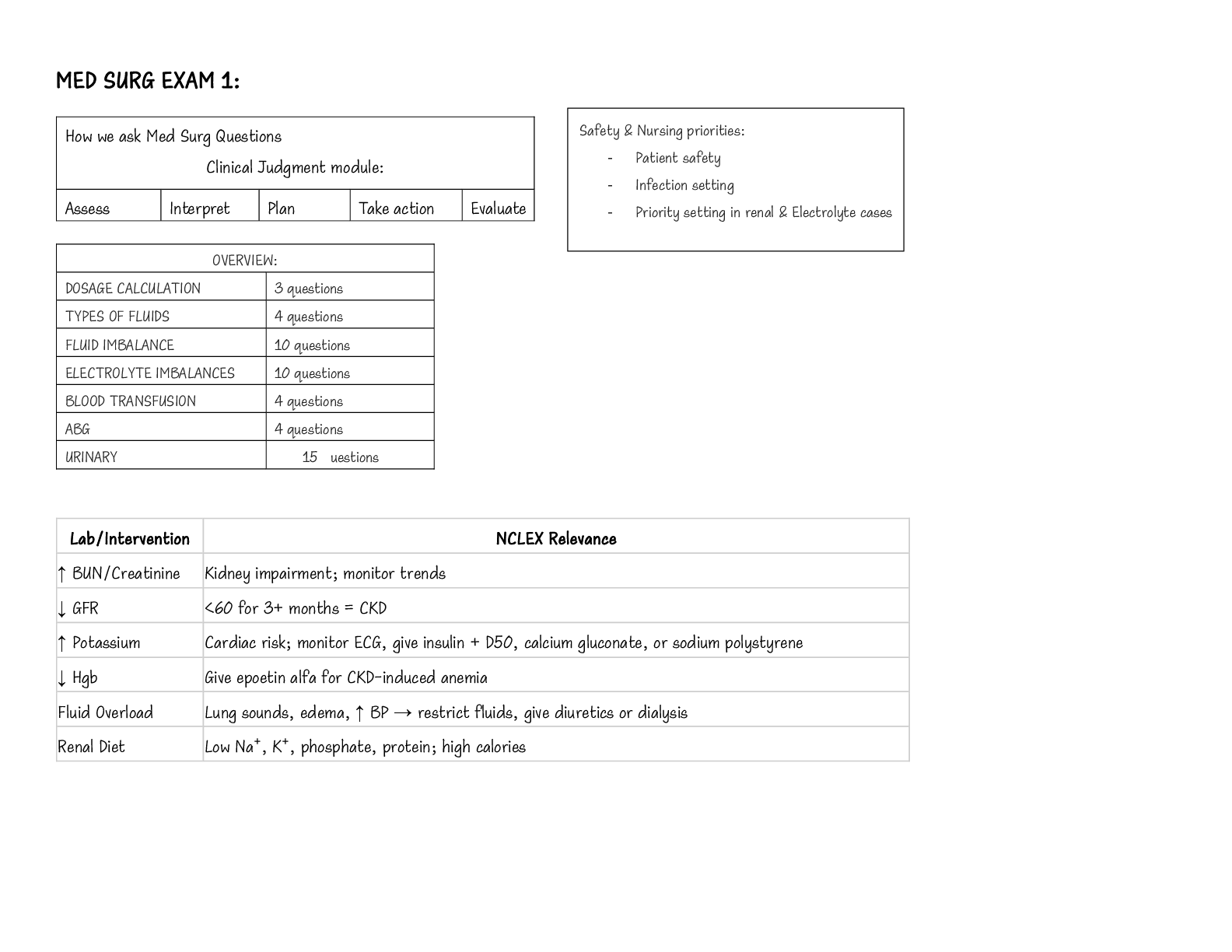
Thermochemistry Worksheet – Energy changes involving phase changes
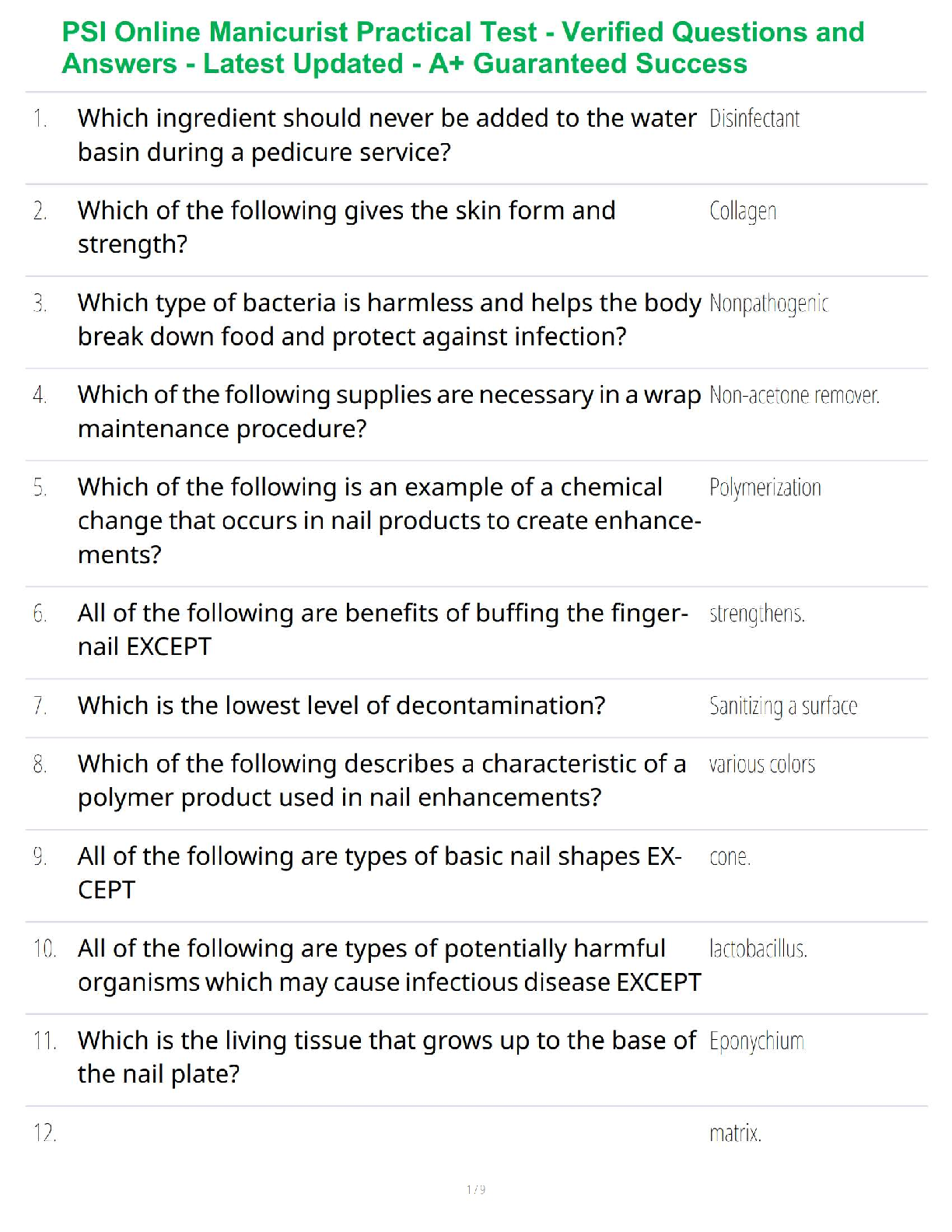
Sample Problem: How much energy is needed to convert 23.0 grams of ice at -10.0°C into steam at 109°C?
When solving problems involving phase changes, i
...
Thermochemistry Worksheet – Energy changes involving phase changes
Sample Problem: How much energy is needed to convert 23.0 grams of ice at -10.0°C into steam at 109°C?
When solving problems involving phase changes, it is helpful to
draw a diagram to visualize the different steps involved.
Each of these steps (1-5) is associated with an energy change that
is reflected in a calculation.
Step 1: If we start by looking at melting a specific amount of ice, the
amount of heat needed to bring the ice up to 0°C is calculated by
the equation ∆ H=mC∆ T with:
∆H = amount of energy (J)
m = mass (grams)
C = specific heat capacity, Cice = 2.10 J/g°C
∆T = change in temperature (°C)
So, for this sample problem: ∆H = 23.0 grams × 2.10 J/g°C × 10°C = 483 J
Step 2: The next step occurs while the ice is melting. There is no temperature change so we cannot use the same equation
as before. A particular amount of ice takes a constant amount of heat to melt it. This energy is used to break those
hydrogen bonds that hold the water in the crystal structure that makes it ice. This amount of heat is called the heat (or
enthalpy) of fusion. Heat of fusion, ∆ Hfus = 334 J/g for water.
23.0 grams × 334 J/g = 7682 J
Step 3: During this step there is a temperature change again, so we use the same equation as in Step 1, ∆H=mC∆T to
calculate the energy changes. However, we are now working with a different state of matter, liquid water, so the specific
heat value is different. Cwater = 4.18 J/g°C. The temperature change is the difference between the melting point and the
boiling point, so 0°C to 100°C.
Solving this step, we get ∆H = 23.0 grams × 4.18 J/g°C × 100°C = 9614 J
Step 4: While the water is boiling, the temperature does not change. The heat of vaporization is the amount of energy it
takes to vaporize a particular quantity of a substance. For water, ∆ Hvap = 2260 J/g.
23.0 grams × 2260 J/g = 51980 J
Step 5: Once the water is in the gas phase, a temperature change occurs again to increase the steam from 100°C to 109°C,
so the equation ∆H=mC∆T is used once more. However, we’re using a different state of matter now, water vapor, so the
specific heat value is Csteam = 1.70 J/g°C.
Solving this last step, ∆H = 23.0 grams × 1.70 J/g°C × 9°C = 351.9 J
Now, add all 5 steps together. At the end you should probably convert to kJ.
483 J (step 1) + 7682 J (step 2) + 9614 J (step 3) + 51980 J (step 4) + 351.9 J (step 5) = 70110.9 J or 70.1 kJ
Not all problems will go through all 5 steps. Diagram it out and choose the appropriate ones
[Show More]