Mathematics > QUESTIONS & ANSWERS > Georgia Institute Of Technology ISYE 6644 Week 12 Homework_ Simulation - ISYE-6644-OAN. (All)

Also available in bundle ( Click Here )

Georgia Institute Of Technology ISYE 6644 Week 12 Homework_ Simulation - ISYE-6644-OAN.

Document Content and Description Below

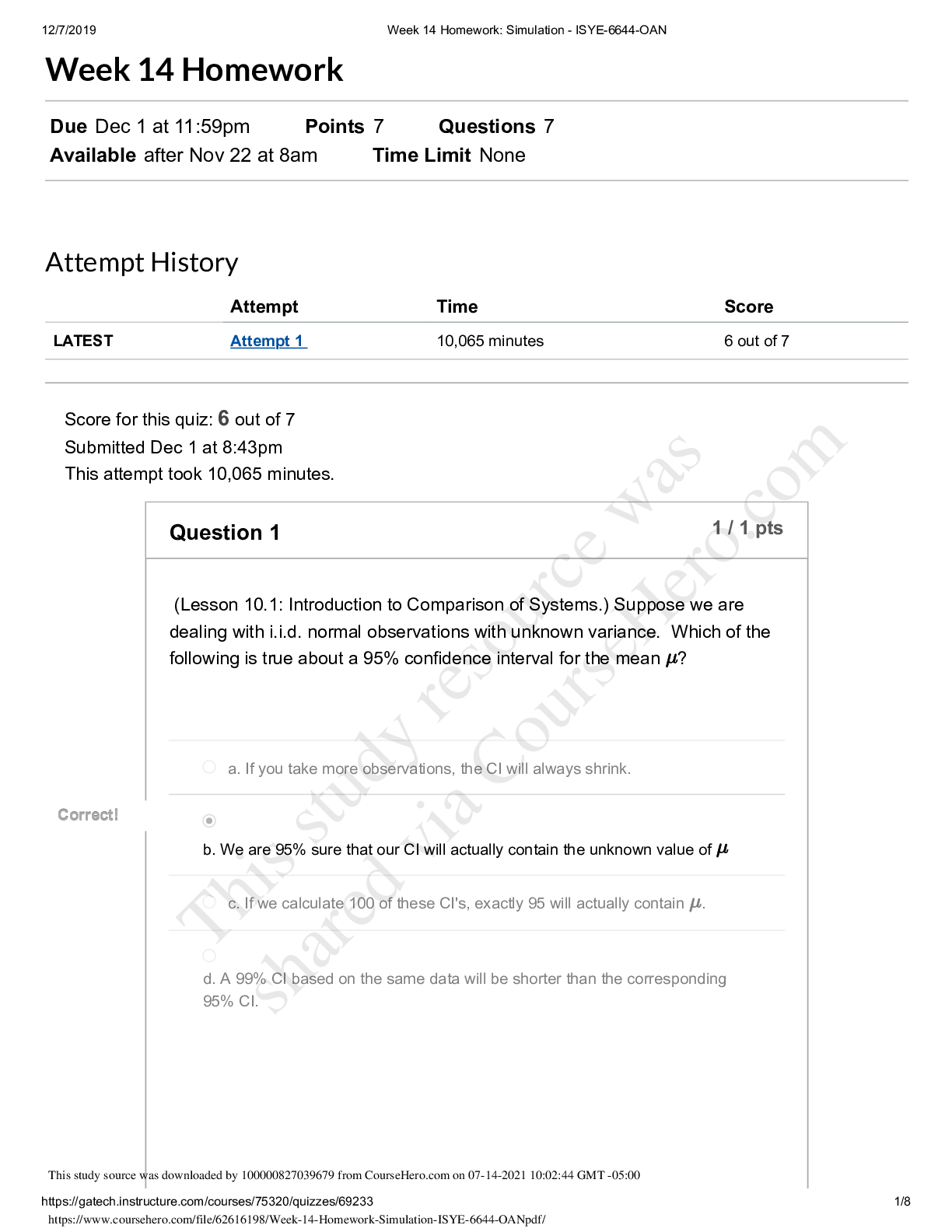
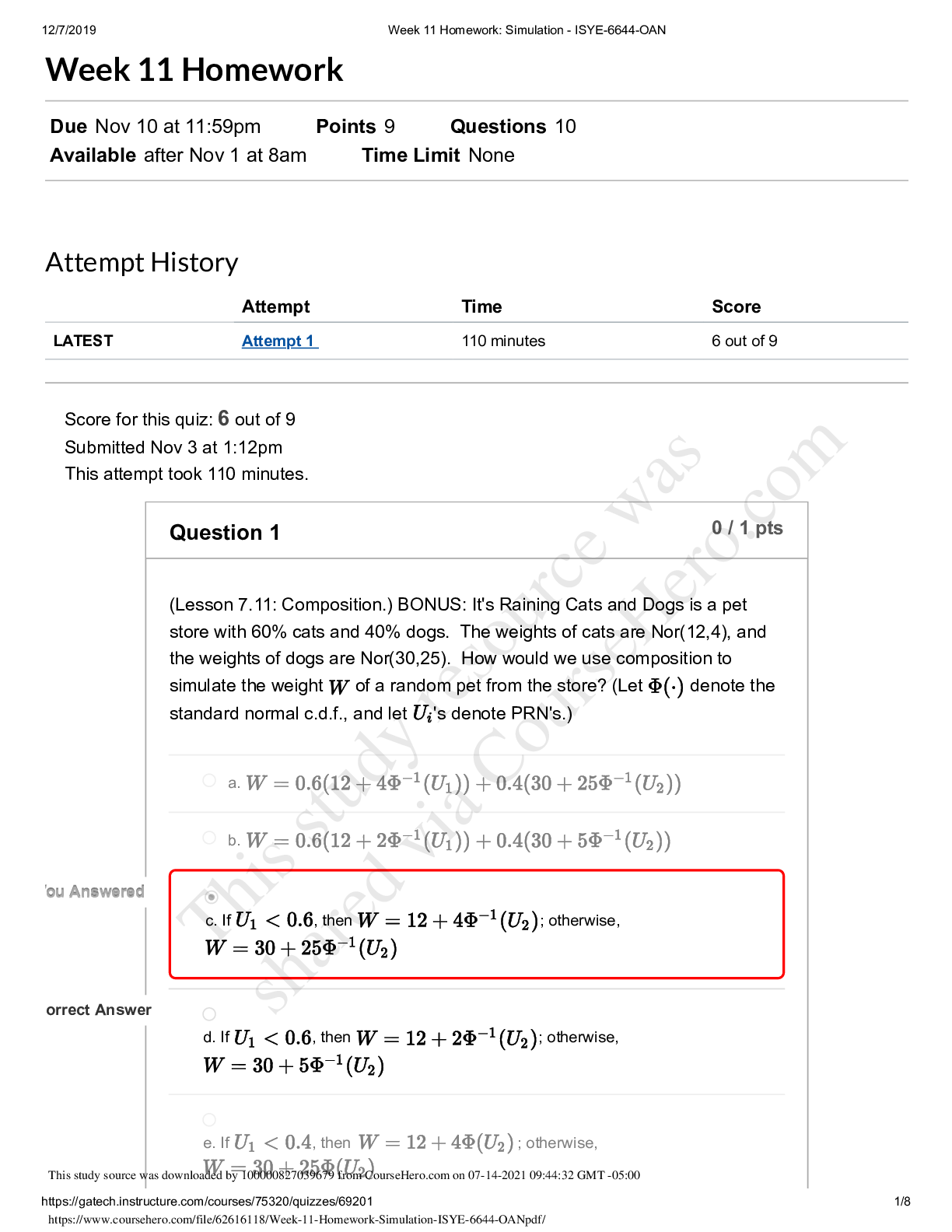
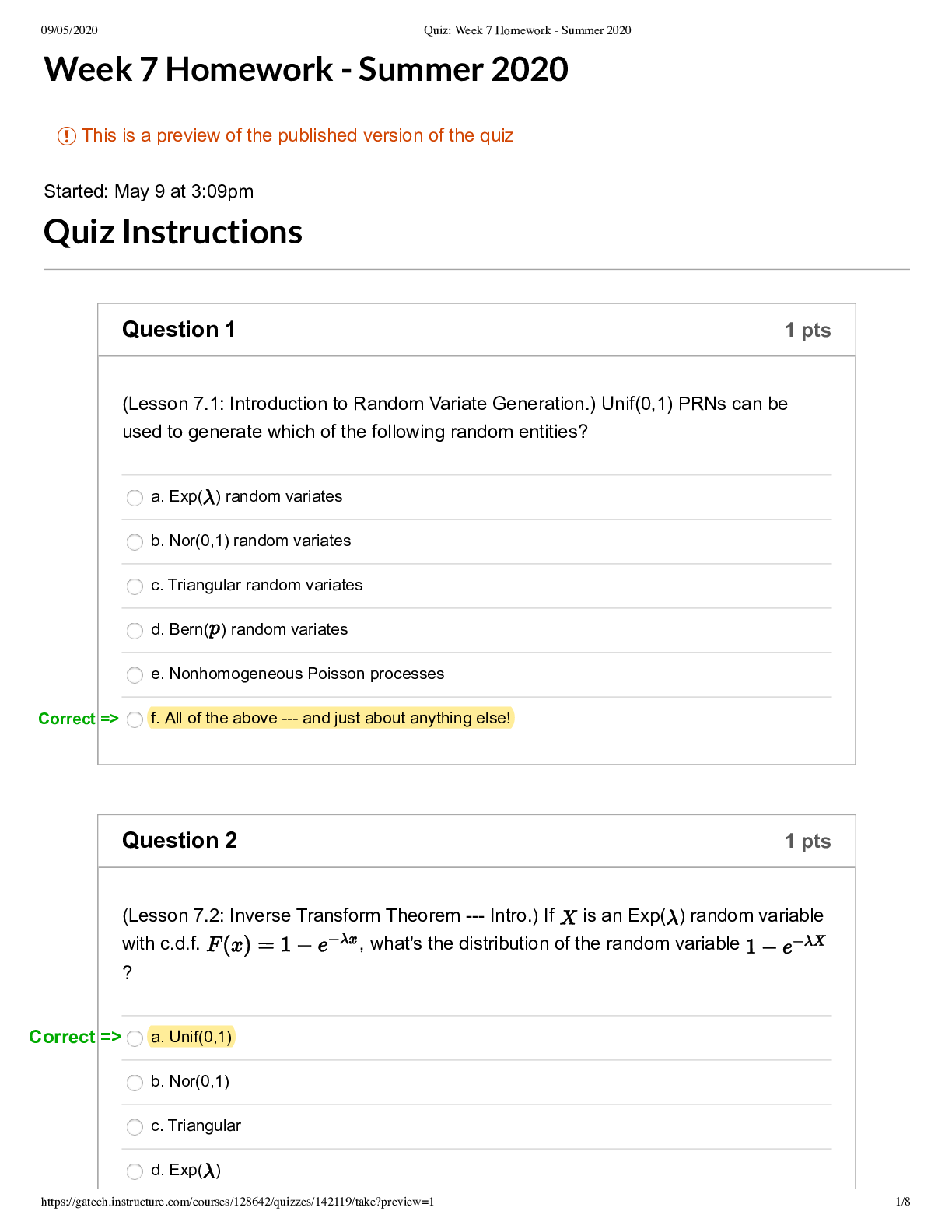
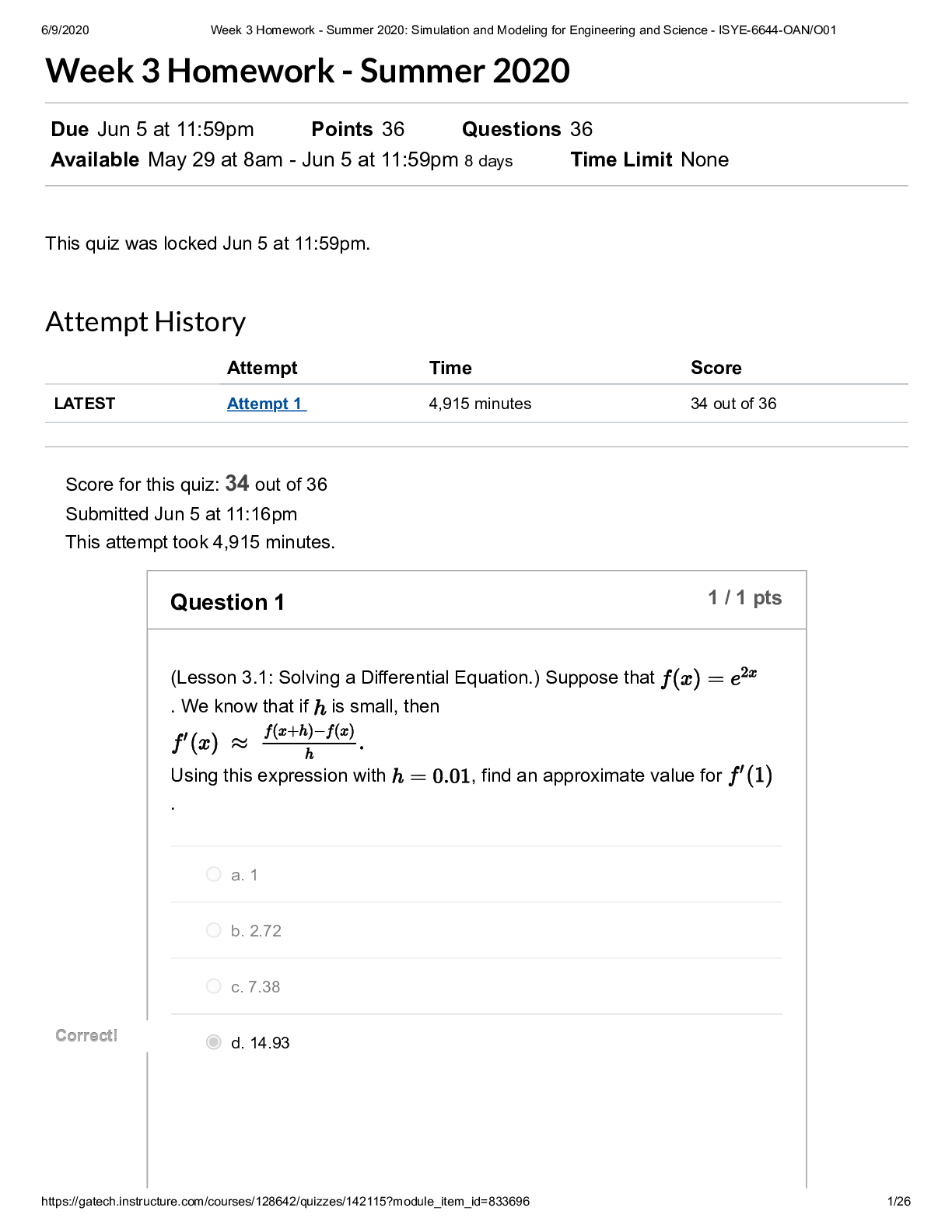
Week 12 Homework Due Nov 17 at 11:59pm Points 17 Questions 17 Available after Nov 8 at 8am Time Limit None Attempt History Attempt Time Score LATEST Attempt 1 1,965 minutes 13 out of 17 Score fo... r this quiz: 13 out of 17 Submitted Nov 17 at 8:18pm This attempt took 1,965 minutes. Question 1 0 / 1 pts (Lesson 8.1: Introduction to Input Modeling.) It's GIGO time! Let's consider an queueing system with Exp( ) interarrivals and Exp( ) FIFO services at a single server. You may recall from some class (either this one or stochastic processes) that the steady-state expected cycle time (i.e., the time that the customer is in the system, including wait + service) is . If you were to try this out in Arena, let's say with interarrivals and services (note the notation change between my usual "Exp" and Arena's ), then we'd get . Go ahead, see for yourself in Arena, but make sure that you run the system for 100,000 or so customers so that you can be sure that you're in steady-state! Finally, here's the GIGO question, which will show what can happen when you mis-model a component of your process: What is the (approximate) steady-state expected cycle time if you have i.i.d. interarrivals instead of interarrivals? Note that both interarrival distributions have the same mean (10), but that doesn't necessarily imply that they'll have the same expected cycle times. Hint: You may want to use Arena as described above.12/7/2019 Week 12 Homework: Simulation - ISYE-6644-OAN https://gatech.instructure.com/courses/75320/quizzes/69213 2/13 a. about 1 Y You Answered ou Answered b. about 10 orrect Answer orrect Answer c. about 23 d. about 40 e. about 62 (c). The case has waaaay smaller tails than the , so it's reasonable to assume that the cycle times will tend to be lower for the case. In fact, after 100,000 customers in Arena, I got an average time of 23.5. Thus, (c) is the right answer. Question 2 1 / 1 pts (Lesson 8.2: Identifying Distributions.) Let's play Name That Distribution! The number of times a "3" comes up in 10 dice tosses. a. Bernoulli Correct! Correct! b. Binomial c. Geometric d. Negative Binomial e. Pareto (b).12/7/2019 Week 12 Homework: Simulation - ISYE-6644-OAN Question 3 1 / 1 pts (Lesson 8.2: Identifying Distributions.) Name That Distribution! The number of dice tosses until a 3 comes up. a. Bernoulli b. Binomial Correct! Correct! c. Geometric d. Negative Binomial e. Pareto (c) [Show More]

Last updated: 2 years ago

Preview 1 out of 13 pages

Buy Now

Instant download

We Accept: