ECE 403/503 Optimization for Machine Learning

ECE 403/503 Optimization for Machine Learning Department of Electrical and Computer Engineering University of Victoria Online link: http://www.ece.uvic.ca/~wslu/403/index.html Office: EOW 427 E-mail: [email protected] ...

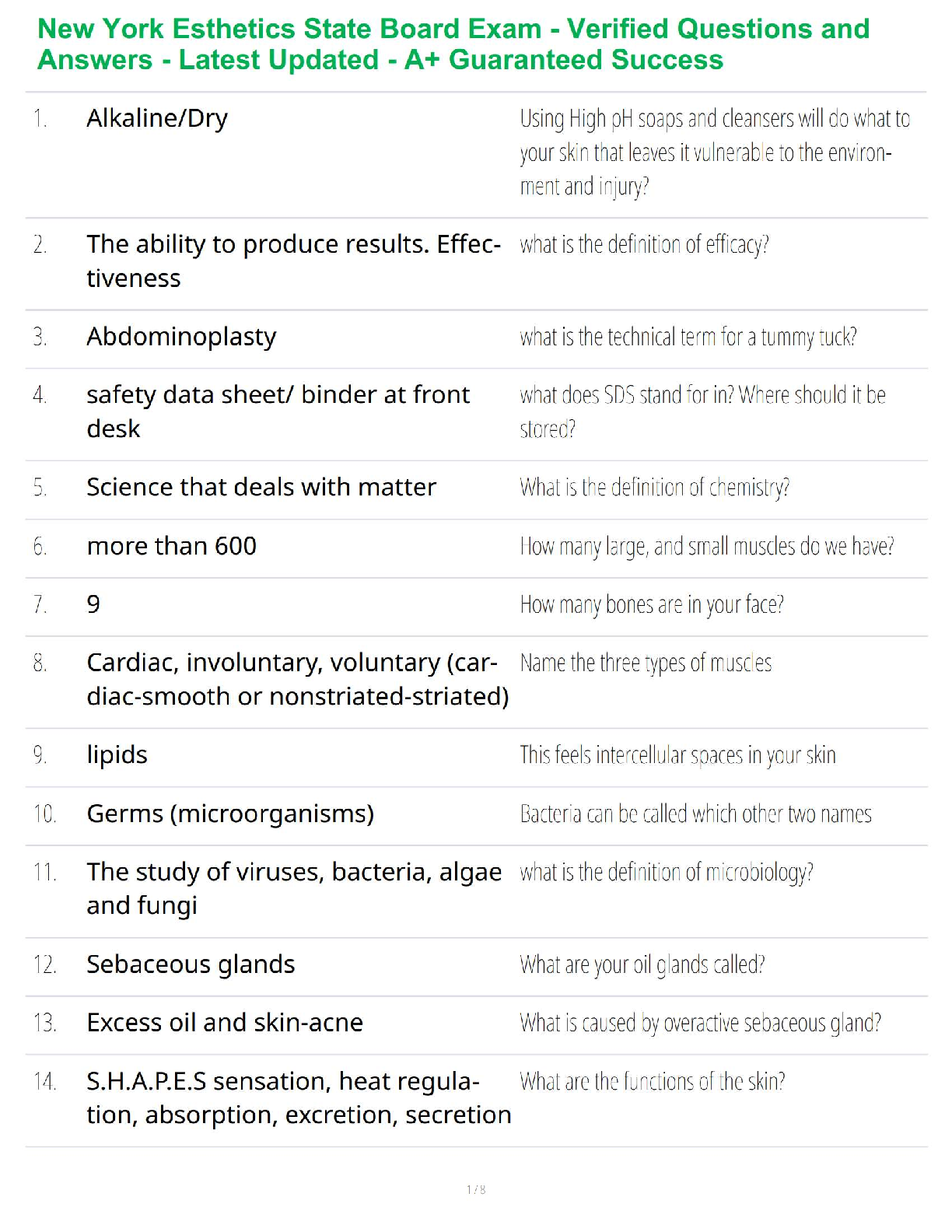
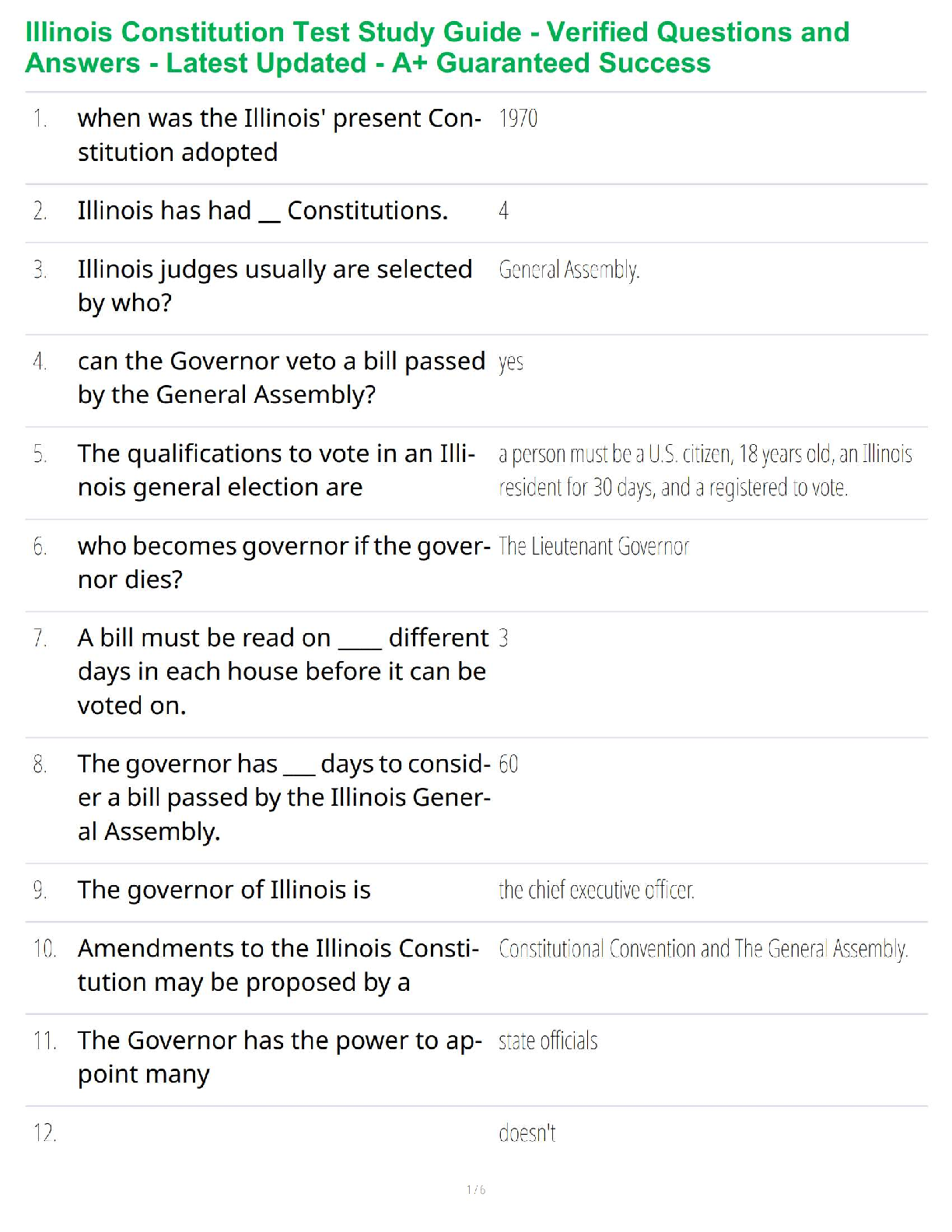
ECE 403/503 Optimization for Machine Learning Department of Electrical and Computer Engineering University of Victoria Online link: http://www.ece.uvic.ca/~wslu/403/index.html Office: EOW 427 E-mail: [email protected] May 20192 Instructor Office Hours Lei Zhao Days: Wednesdays Phone: 778-967-2019 Time: 15:00 – 17:00 E-mail: [email protected] Location: EOW 419 URL: http://studentweb.uvic.ca/~leizhao Lectures Days: Tuesday, Wednesday, Friday Time: 1:30 – 2:20pm Location: Engineering Computer Science Building (ECS) A108 Labs for ECE 403 & 503 B01 Thu, 2:30-5:20 pm, ELW326, Sep 26, Oct 10, Oct 31, Nov 21 Required Text Course Notes Assessment Assignments: 10% Labs (for ECE 403) 15% Labs & Project (for ECE 503) 15% Mid-term exam 20% Date: Wednesday, October 30, 13:30-14:20 Final exam 55% Other Things to Note • Course web site: http://studentweb.uvic.ca/~leizhao/403.html. • About assignments: - There will be 7 assignments. - Only paper copies are accepted. - Please clearly print your name and V-number on the first page of your work. - Submit your assignment on the due day by 4:00 pm. 2 submission options: ◊ Submit your work to the instructor at class; or ◊ Drop it into the drop box. References Requirement Software3 Chapter 1 Optimization Problems in Machine Learning 1.1 Optimization Problems 1.2 Types of Data Sets 1.3 Feature Extraction 1.4 Examples of Unsupervised Learning 1.5 Examples of Supervised Learning Problems Chapter 2 Basic Concepts and Optimization Algorithms 2.1 Gradient and Hessian 2.2 Optimality Conditions 2.3 Gradient Descent Algorithm 2.4 Accelerated Gradient Algorithms 2.5 Stochastic Gradient Algorithms 2.6 Newton Algorithm 2.7 Quasi-Newton Algorithms Problems Chapter 3 Applications in Machine Learning 3.1 Classification by Minimizing Hinge Loss 3.2 Softmax Regression 3.3 Kernel Methods Problems Appendix A Basic Principles and Techniques of Linear Algebra Appendix B Elements of Probability Theory4 References [1] L. Bottou, F. E. Curtis, and J. Nocedal, “Optimization methods for machine learning,” SIAM Review, vol. 60, no. 2, pp. 223-311, 2018. [2] Y. LeCun, C. Cortes, and C. J. C. Burges, “The MNIST database,” see the web link: http://yann.lecun.com/exdb/mnist/ [3] UCI Machine Learning, http://archive.ics.uci.edu/ml, University of California Irvine, School of Information and Computer Science. [4] C. M. Bishop, Neural Networks for Pattern Recognition, Clarendon Press, Oxford, 1995. [5] G. H. Golub and C. F. Van Loan, Matrix Computations, 2nd ed., Johns Hopkins University Press, 1989. [6] D. D. Lee and H. S. Seung, “Learning the parts of objects by non-negative matrix factorization,” Nature, vol. 401, pp. 788–791, 21Oct. 1999. [7] N. Gillis, “The why and how of nonnegative matrix factorization,” in Regularization, Optimization, Kernels, and Support Vector Machines, J. A. K. Suykens, M. Signoretto, and A. Argyriou Eds., pp. 257-291, CRC Press, 2014. [8] T. Hastie, R. Tibshirani, and J. Friedman, The Elements of Statistical Learning, 2nd ed., Springer, 2009. [9] A. Antoniou and W.-S. Lu, Practical Optimization – Algorithms and Engineering Applications, Springer 2007. [10] S. Boyd and L. Vandenberghe, Convex Optimization, Cambridge University Press, 2004. [11] Y. Nesterov, “A method for solving a convex programming problem with rate of convergence O(1/k2),” Soviet Math. Doklady, vol. 269, no. 3, pp. 543–547, 1983, in Russian. [12] Y. Nesterov, Introductory Lectures on Convex Optimization — A Basic Course, Norwell, MA.: Kluwer Academic Publishers, 2004. [13] M. Grant and S. Boyd, CVX: MATLAB Software for Disciplined Convex Programming, version 2.0, Sept. 2013, online available: http://cvxr.com/cvx [14] C. M. Bishop, Pattern Recognition and Machine Learning, Springer, 2006. [15] W. N. Street, W. H. Wolberg, and O. L. Mangasarian, “Nuclear feature extraction for breast tumor diagnosis,” in IS?T/SPIE Int. Symp. Electronic Imaging: Science and Technology, vol. 1905, pp. 861-870, San Jose, CA., 1993. [16] O. L. Mangasarian, W. N. Street, and W. H. Wolberg, “Breast cancer diagnosis and prognosis via linear programming,” AAAI Tech. Report SS-94-01, 1994.5 • Requirements (a) The mathematical literacy for taking this cause includes ◊ basic linear algebra (MATH 101) ◊ calculus (MATH 100, 101, and 200) ◊ basic probability theory (STAT 254) (b) Software ◊ Familiarity with MATLAB is essential for better understanding course material, doing homework, performing laboratory experiments, conducting projects, and so on. Occasionally we use CVX. CVX is a MATLAB software for disciplined convex optimization. Assuming you have properly installed MATLAB on your PC, you can download and install and use CVX on your computer as a MATLAB toolbox. ◊ To download CVX, go to the web link http://cvxr.com/cvx/download/ , read the instructions carefully, choose an appropriate download option and follow the installation steps exactly. An informative user guide for version 2.1 of the software is available from the web link below: http://web.cvxr.com/cvx/doc/ ◊ Both MATLAB and CVX are available on the PCs in the laboratory room. It is a great idea to install these software packages on your personal computer as well for the convenience of using the software elsewhere.6 Chapter 1 Optimization Problems in Machine Learning 1.1 Optimization Problems The world is so much quantified these days. And we are told that we now live in a “big data” era as search engines, recommendation platforms, and speech and image recognition software become an indispensable part of modern society. Based on statistical techniques and by capitalizing on increasingly powerful computing resources and availability of datasets of immense size, machine learning (ML) has demonstrated a dramatic rise by playing a key role in many recent technological advances that yield undeniable performance superiority as well as societal, economic, and scientific impacts [1]. From a technical perspective, ML focuses on the development of computer programs that can access data and use it to learn for themselves. The process of learning begins with observations or data, such as examples, direct experience, or instruction, in order to look for patterns in data and make better decisions in the future (often in terms of unseen data), based on the examples provided. In brief words, ML allows computers to learn automatically without human intervention or assistance and adjust actions accordingly. One of the pillars of ML is mathematical optimization which, in this context, involves numerical computations of parameters for a system designed to make decisions based on available data. During the optimization process, these parameters are chosen to be optimal with respect to a given learning problem [1]. ML applications deal with a large variety of data sizes, types and structures, as well as a suite of criteria for performance evaluations. As a result, the problem sizes as well as the formulations and solution techniques can vary wildly from standard leastsquares to highly nonlinear and nonconvex optimization methods. Nevertheless, practically all optimization problems for ML applications fit into the general formulation minimize ( ) (1.1a) subject to: ( ) 0 for 1,2, , (1.1b) ( ) 0 i j f a i p c    x x x for 1,2, , j q  (1.1c) where f ( ) x is an objective (or loss) function, ai( ) 0 x  for i = 1, 2, …, p are equality constraints, cj( ) 0 x  for j = 1, 2, …, q are inequality constraints. According to (1.1), optimization is an algorithmic procedure for identifying a best set of parameters as vector x that reduces the loss (measure by function f ( ) x ) to minimum while meeting all the requirements that are set for x to satisfy. This course is about basic concepts and optimization methods that are found particularly useful for ML applications. Our primary goal is to address the following two questions: 1. How do optimization problems arise in ML applications? 2. What are the most successful optimization methods for ML problems of various scales? The first question is addressed in the rest of this chapter, while