Mathematics > MILESTONE > SoPhia Learning, Unit 3, Practice Milestone 3 WITH ANSWERS (All)

SoPhia Learning, Unit 3, Practice Milestone 3 WITH ANSWERS

Document Content and Description Below

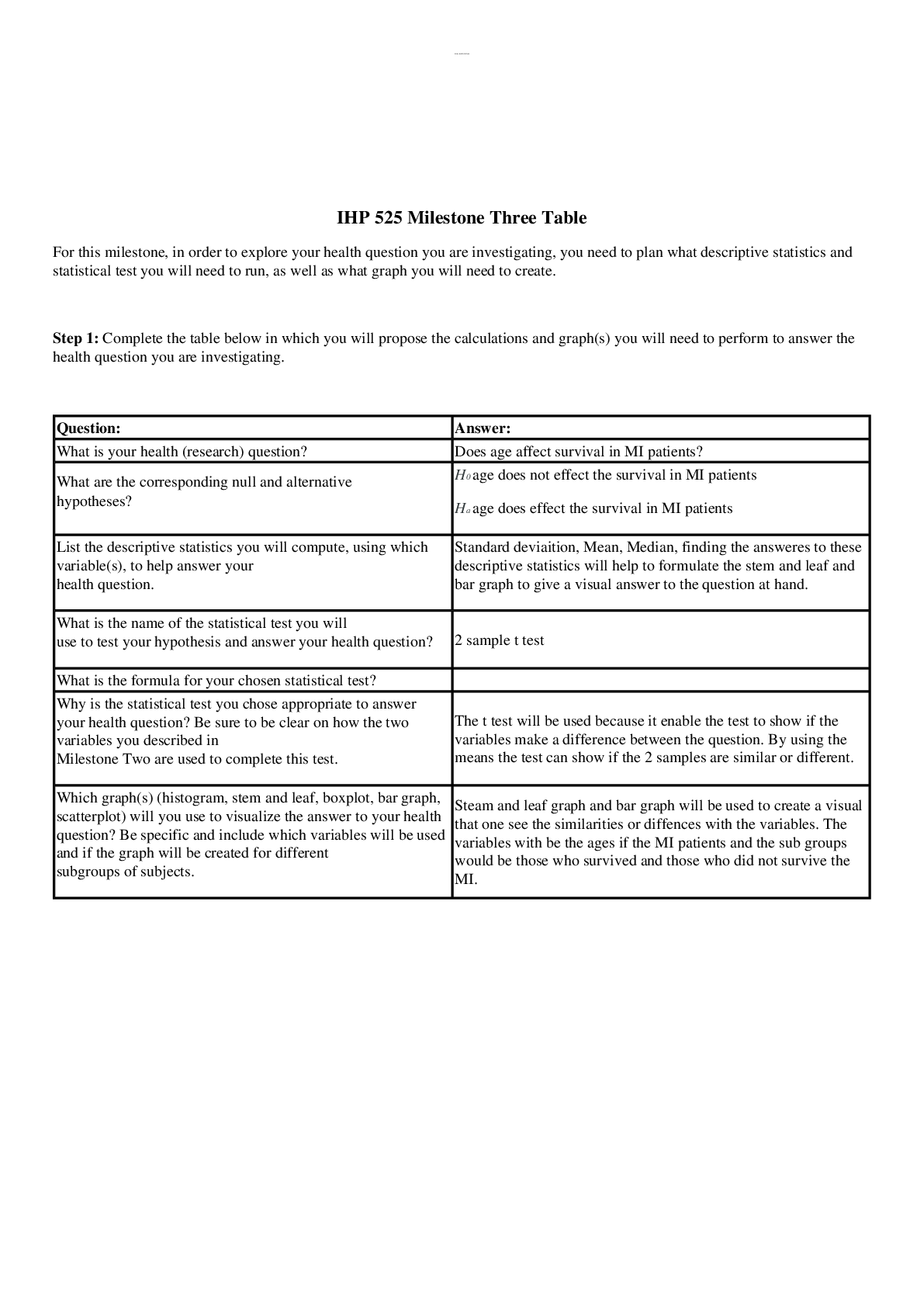
SoPhia Learning, Unit 3, Practice Milestone 3 WITH ANSWERS 1 Match each equation with the corresponding slope and intercept. D B A C • A. • B. • • C. • 2 of 59 • D. • RATI ... ONALE When the coordinates are plugged into the formula, evaluate the subtraction in the numerator and the denominator. 7 minus 2 is 5, which becomes the value of the numerator. 3 minus 3 is 0, which becomes the value of the denominator. However, because we cannot divide by 0, the slope is undefined. The line is a vertical line where x always equals 3. It intercepts the x-axis at (3,0). For the line , we can identify any two points and calculate the slope. If the equation is , that means for any point on the line, the x-coordinate will be 3. For example, two points may be (3,2) and (3,7). We can use the slope formula and plug in the appropriate values. For the line , we can identify any two points and calculate the slope. If the equation is , that means for any point on the line, the y-coordinate will be 3. For example, two points may be (1,3) and (9,3). We can use the slope formula and plug in the appropriate values. 3 of 59 When the coordinates are plugged into the formula, evaluate the subtraction in the numerator and the denominator. 3 minus 3 is 0, which becomes the value of the numerator. 9 minus 1 is 8, which becomes the value of the denominator. Dividing 0 by 8 equals 0. The slope of this line is 0. The line is a horizontal line where y always equals 3. It intercepts the y-axis at (0,3). The variable is the coefficient in front of x that represents the slope. In the equation , the coefficient in front of x is -2, so -2 is the slope. The variable represents the y-coordinate of the yintercept. In the equation , 2 will be the ycoordinate of the y-intercept. Remember that the xcoordinate of the y-intercept is always 0, so the y-intercept is (0,2). For the line , we can identify the slope and yintercept because it is in slope-intercept form: . For the line , we can identify the slope and yintercept because it is in slope-intercept form: . 4 of 59 CONCEPT Forms of Linear Equations 2 The graph of a function is shown here. The variable is the coefficient in front of x that represents the slope. In the equation , the coefficient in front of x is , so this is the slope. The variable represents the y-coordinate of the yintercept. In the equation , -1 will be the ycoordinate of the y-intercept. Remember that the xcoordinate of the y-intercept is always 0, so the yintercept is (0,-1). [Show More]

Last updated: 3 years ago

Preview 1 out of 59 pages

Buy Now

Instant download

We Accept: