University of California, Los Angeles LIFESCIENC 30A. LS30A MATHEMATICS FOR LIFE SCIENTISTS. S Venugopal LS 30A (Spring 2020) June 08, 2020 Final Exam. Solutions

Document Content and Description Below

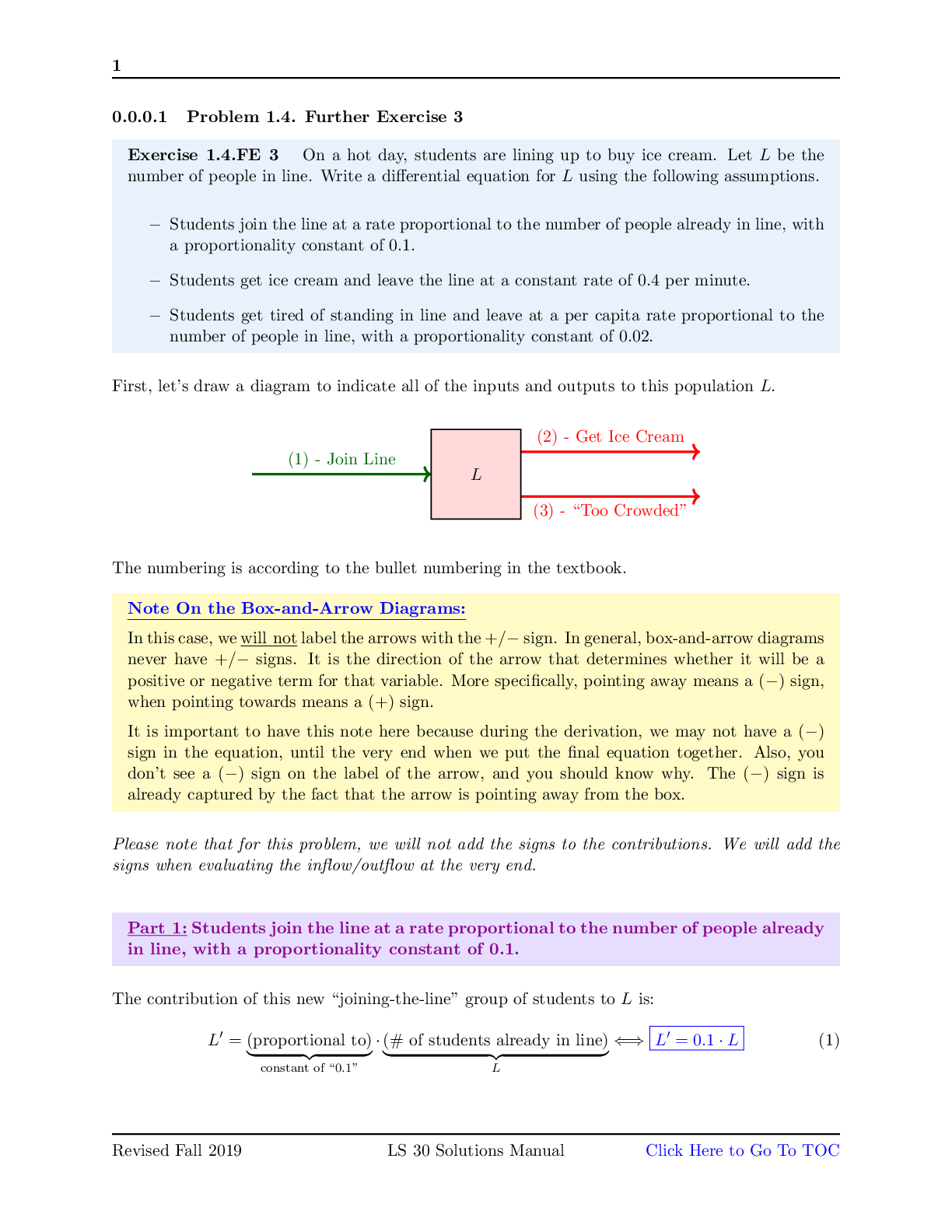
S Venugopal LS 30ACS Venugopal LS 30A (Spring 2020) June 08, 2020 Final Exam Use dark colored pen only to write your answers. Duration of the exam: 6:30 PM PDT, Monday, June 8, 2020 TO 6:30 PM PD... T, Tuesday, June 9, 2020. Where is the exam? The exam PDF is available on CCLE in the Exam Material section. Where should I upload my answers? Your exam may be uploaded as a single PDF on to the final exam assignment on CCLE. No Gradescope submission is required. Is anyone proctoring the exam in case I have a question? No one is proctoring your exam. However, you can ask questions about the exam *publicly* on campuswire. DO NOT send specific emails to either Dr. V or Vijay or Ricky. Your LAs are NOT proctors, so DO NOT bother them! What if I need to speak with Dr. V privately? Dr. V is available on zoom room between 10 – 11 AM on Tuesday, June 9th. Same as synchronous lecture on CCLE. (Meeting ID: 752 407 055; Password: LS30A) Please do not write below this line PART-1: Modeling using differential equations 1. [20 points] The COVID-19 pandemic which made our lives miserable this Spring quarter is an excellent example of a dynamical system (i.e., systems that change over time). Here, you will develop a differential equation model for exploring the epidemiology of this pandemic based on the following assumptions. • In this model, S represents susceptible individuals and I represents infected individuals. These are the only two populations that you will need to consider. • Infection rate tells you how quickly susceptible individuals are becoming infected. The per-capita infection rate of S is proportional to the number of infected people with a constant of proportionality, b. • The more the number of I’s at any given time, the harder it is to provide timely medical care and therefore more infected people are likely to die. You can model the per-capita death rate of infected individuals as a sigmoid function of the infected population. Feel free to make up parameters, as necessary. • You can assume that a constant number of individuals = 2 are added to the population of S, each time unit. Write a differential equation model based on the above assumptions. 2. The following system of differential equations models a food-chain, where X eats Y, and Y. a) [12 points] Draw an inflow/outflow diagram for the above model showing each inflow and outflow for each state variable. b) [14 points] List all the parameters of this model. c) [12 points] Describe the model assumptions in your own words. Make sure that you state the per capita rates with relevant parameters and as functions of the state variables where appropriate. d) [5 points] Identify any feedback loop that can arise from the interactions between the variables in the above model. PART-2: Derivatives, integrals and their application 3. a) [10 points] Using the idea of ???????? = ??????? ???? , explain the meaning of “derivative”. You can draw a graph to describe it geometrically using secant and tangent lines OR use the idea of average and instantaneous rates of change OR you can use both methods. b) [10 points] Using the same idea of velocity, explain how you can obtain distance covered given velocity as a function of time. Again, you can use graphs, notations, geometric shapes like rectangles to describe this. What is this mathematical process called? (Hint: Look at the title of PART-2 above). c) [5 point] Briefly explain the ‘Fundamental Theorem of Calculus’ using words, notations and/or a figure as appropriate. d) [10 points] Find the derivative of the following function at ? = 0, and ? = 2. (Derivative rules provided at the end of the exam). e) [10 points] Approximate the area under the graph of ?(?) = ?2 + 2 between ? = 1 and ? = 3 using ∆? = 0.5. a) [10 points] First, give your answer in the form ∆? = ?. ∆? b) [16 points] Expand your answer from part (a) by rewriting ∆? as ?(?) - ?(?0) and ∆? as ? - ?0, and solving for ?(?). Make sure to evaluate ?(?0). c) [10 points] Now, approximate ?(2) based on the expression from part (b). d) [10 points] Write down the equation of the tangent line of ?(?) at ?0 = 0. Hint: Use your answer from part (b). 6. For the following models, the change equations and state-space with nullclines are already drawn. PART-4: Bifurcation of Equilibria: Qualitative changes in system behavior 8. Elon Musk, the developer of the Tesla electric car announced that he would release all the patents of his company, free of charge. This certainly created market for electric cars and car companies like BMW, Chevy, Honda, Nissan and others adopted the technology. If we represent the number of electric car models in the market using a variable X, the rate of change of X can be modeled using a logistic growth model with allee effect as follows: where, r is the maximum growth rate, k is the carrying capacity of the market. a) [10 points] Suppose a=2, k=10 and r=1. Say, Elon Musk had made a selfish decision of not releasing the patents and Tesla was the ONLY electric car company. Would Musk’s decision gain him market supremacy in the long run? Explain using a phase portrait. d) [10 points] Briefly explain the market for electric cars based on the bifurcation diagram below. Make sure to note any bistability in the system. 9. Melanin is a pigment in our skin that protects us from skin damage due to sun exposure. A startup biotech company is testing melanin-treatment for skin cancer. They make a mathematical model to design a treatment strategy. In the bifurcation diagram given below, ?∗ represents the final melanin count at the end of the treatment and ? represents a parameter controlling the treatment dosage. Healthy skin requires melanin levels to lie between 107 and 109. Answer the following questions to aid in the design of a clinical trial. a) [15 points] List the bifurcations that occur in this diagram. For each one, state what type of bifurcation it is and at what value of ? it occurs. b) [5 points] Patient-1 comes with an abnormally low melanin count of 105. Clinician A suggests a ? = 10 for treatment. Reason if this is a good strategy or not to restore normal levels of melanin? c) [5 points] Patient-2 comes with an initial low melanin count of 106. Clinician B suggests a treatment with ? = 30, but noticed that this did not restore healthy melanin levels. Instead, it made the melanin count even lower. Why isn’t this treatment working? d) [10 points] Using the concept of bifurcations, help the clinicians to come up with a range of ? values that can restore normal levels of melanin for both patients 1 and 2. PART-5: Various concepts learned throughout LS30A 10. Provide concise answers to the following: a) [16 points] Explain what is wrong with the following. (i) ?2 = ?2 is a function. b) [10 points] Match the time series to the corresponding trajectory in state space. The black dot/circle in the state space is the initial condition. c) [10 points] Use Euler’s method to simulate the following model for two time steps starting with an initial condition of (?0, ?0) = (1, 2) and a step size of 0.1.. Final Exam Use dark colored pen only to write your answers. Duration of the exam: 6:30 PM PDT, Monday, June 8, 2020 TO 6:30 PM PDT, Tuesday, June 9, 2020. Where is the exam? The exam PDF is available on CCLE in the Exam Material section. Where should I upload my answers? Your exam may be uploaded as a single PDF on to the final exam assignment on CCLE. No Gradescope submission is required. Is anyone proctoring the exam in case I have a question? No one is proctoring your exam. However, you can ask questions about the exam *publicly* on campuswire. DO NOT send specific emails to either Dr. V or Vijay or Ricky. Your LAs are NOT proctors, so DO NOT bother them! What if I need to speak with Dr. V privately? Dr. V is available on zoom room between 10 – 11 AM on Tuesday, June 9th. Same as synchronous lecture on CCLE. (Meeting ID: 752 407 055; Password: LS30A) Please do not write below this line PART-1: Modeling using differential equations 1. [20 points] The COVID-19 pandemic which made our lives miserable this Spring quarter is an excellent example of a dynamical system (i.e., systems that change over time). Here, you will develop a differential equation model for exploring the epidemiology of this pandemic based on the following assumptions. • In this model, S represents susceptible individuals and I represents infected individuals. These are the only two populations that you will need to consider. • Infection rate tells you how quickly susceptible individuals are becoming infected. The per-capita infection rate of S is proportional to the number of infected people with a constant of proportionality, b. • The more the number of I’s at any given time, the harder it is to provide timely medical care and therefore more infected people are likely to die. You can model the per-capita death rate of infected individuals as a sigmoid function of the infected population. Feel free to make up parameters, as necessary. • You can assume that a constant number of individuals = 2 are added to the population of S, each time unit. Write a differential equation model based on the above assumptions. 2. The following system of differential equations models a food-chain, where X eats Y, and Y. a) [12 points] Draw an inflow/outflow diagram for the above model showing each inflow and outflow for each state variable. b) [14 points] List all the parameters of this model. c) [12 points] Describe the model assumptions in your own words. Make sure that you state the per capita rates with relevant parameters and as functions of the state variables where appropriate. d) [5 points] Identify any feedback loop that can arise from the interactions between the variables in the above model. PART-2: Derivatives, integrals and their application 3. a) [10 points] Using the idea of ???????? = ??????? ???? , explain the meaning of “derivative”. You can draw a graph to describe it geometrically using secant and tangent lines OR use the idea of average and instantaneous rates of change OR you can use both methods. b) [10 points] Using the same idea of velocity, explain how you can obtain distance covered given velocity as a function of time. Again, you can use graphs, notations, geometric shapes like rectangles to describe this. What is this mathematical process called? (Hint: Look at the title of PART-2 above). c) [5 point] Briefly explain the ‘Fundamental Theorem of Calculus’ using words, notations and/or a figure as appropriate. d) [10 points] Find the derivative of the following function at ? = 0, and ? = 2. (Derivative rules provided at the end of the exam). e) [10 points] Approximate the area under the graph of ?(?) = ?2 + 2 between ? = 1 and ? = 3 using ∆? = 0.5. a) [10 points] First, give your answer in the form ∆? = ?. ∆? b) [16 points] Expand your answer from part (a) by rewriting ∆? as ?(?) - ?(?0) and ∆? as ? - ?0, and solving for ?(?). Make sure to evaluate ?(?0). c) [10 points] Now, approximate ?(2) based on the expression from part (b). d) [10 points] Write down the equation of the tangent line of ?(?) at ?0 = 0. Hint: Use your answer from part (b). 6. For the following models, the change equations and state-space with nullclines are already drawn. PART-4: Bifurcation of Equilibria: Qualitative changes in system behavior 8. Elon Musk, the developer of the Tesla electric car announced that he would release all the patents of his company, free of charge. This certainly created market for electric cars and car companies like BMW, Chevy, Honda, Nissan and others adopted the technology. If we represent the number of electric car models in the market using a variable X, the rate of change of X can be modeled using a logistic growth model with allee effect as follows: where, r is the maximum growth rate, k is the carrying capacity of the market. a) [10 points] Suppose a=2, k=10 and r=1. Say, Elon Musk had made a selfish decision of not releasing the patents and Tesla was the ONLY electric car company. Would Musk’s decision gain him market supremacy in the long run? Explain using a phase portrait. d) [10 points] Briefly explain the market for electric cars based on the bifurcation diagram below. Make sure to note any bistability in the system. 9. Melanin is a pigment in our skin that protects us from skin damage due to sun exposure. A startup biotech company is testing melanin-treatment for skin cancer. They make a mathematical model to design a treatment strategy. In the bifurcation diagram given below, ?∗ represents the final melanin count at the end of the treatment and ? represents a parameter controlling the treatment dosage. Healthy skin requires melanin levels to lie between 107 and 109. Answer the following questions to aid in the design of a clinical trial. a) [15 points] List the bifurcations that occur in this diagram. For each one, state what type of bifurcation it is and at what value of ? it occurs. b) [5 points] Patient-1 comes with an abnormally low melanin count of 105. Clinician A suggests a ? = 10 for treatment. Reason if this is a good strategy or not to restore normal levels of melanin? c) [5 points] Patient-2 comes with an initial low melanin count of 106. Clinician B suggests a treatment with ? = 30, but noticed that this did not restore healthy melanin levels. Instead, it made the melanin count even lower. Why isn’t this treatment working? d) [10 points] Using the concept of bifurcations, help the clinicians to come up with a range of ? values that can restore normal levels of melanin for both patients 1 and 2. PART-5: Various concepts learned throughout LS30A 10. Provide concise answers to the following: a) [16 points] Explain what is wrong with the following. (i) ?2 = ?2 is a function. b) [10 points] Match the time series to the corresponding trajectory in state space. The black dot/circle in the state space is the initial condition. c) [10 points] Use Euler’s method to simulate the following model for two time steps starting with an initial condition of (?0, ?0) = (1, 2) and a step size of 0.1.. [Show More]

Last updated: 2 years ago

Preview 1 out of 13 pages